Следующим
шагом необходимо кубические функции Эрмита сделать более удобными для
использования на практике. Производная 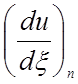 ,
определенная в узле n,
зависит от координаты x
данного элемента и двух соседних элементов. Поэтому удобно определить
глобальную производную
,
определенная в узле n,
зависит от координаты x
данного элемента и двух соседних элементов. Поэтому удобно определить
глобальную производную 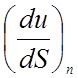 , а затем
использовать следующую взаимосвязь:
, а затем
использовать следующую взаимосвязь:
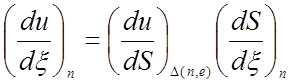 , (25)
, (25)
где 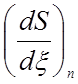 –
масштабный коэффициент элемента, который задает масштаб производной в
глобальном узле D по отношению к
производной по x в
узле n элемента. В результате
производная
–
масштабный коэффициент элемента, который задает масштаб производной в
глобальном узле D по отношению к
производной по x в
узле n элемента. В результате
производная ![]() оказывается непрерывной на границах
элемента.
оказывается непрерывной на границах
элемента.
Двумерные базисные функции Эрмита требуют уже четыре производных на один узел:
u, 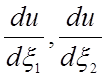 и
и
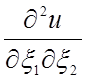 . (26)
. (26)
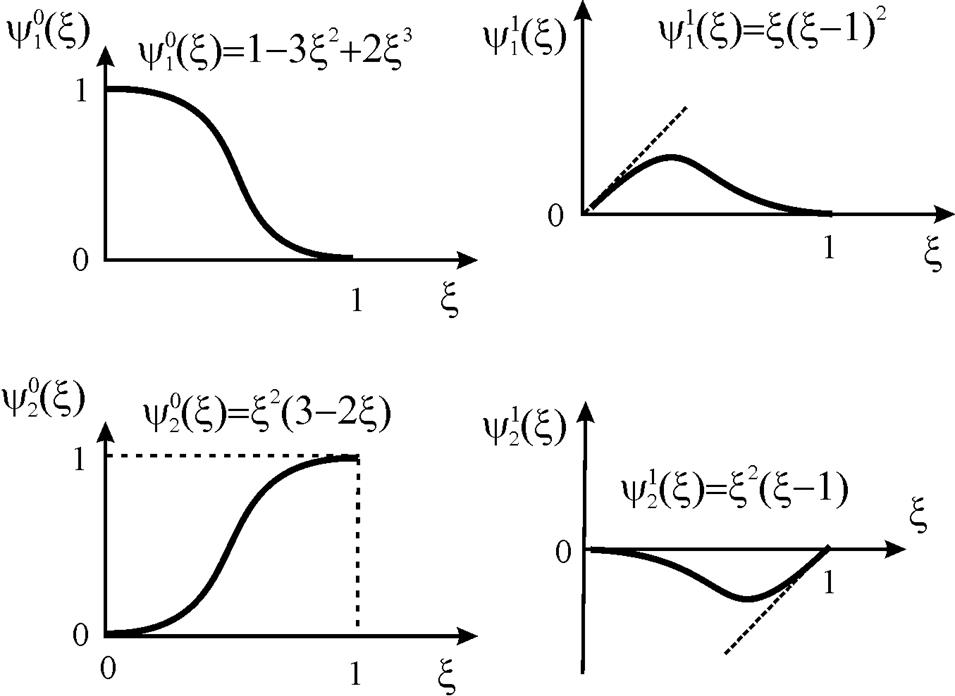
Рис. 12. Кубические функции Эрмита
Наличие
смешанной производной второго порядка объясняется следующим образом: если
величина u пропорциональна x13 и
x23,
то производная ![]() будет пропорциональна x12 и
x23,
а
будет пропорциональна x12 и
x23,
а 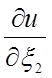 будет пропорциональна x13
и x22,
будет пропорциональна x13
и x22,
Рассмотрим
подробнее интерполяцию производной ![]() вдоль
направления 1-3 (рис. 13). Кубическая зависимость u от x2 определена для дополнительных четырех
узловых параметров. Два из них определены производными
вдоль
направления 1-3 (рис. 13). Кубическая зависимость u от x2 определена для дополнительных четырех
узловых параметров. Два из них определены производными 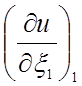 и
и
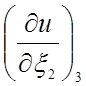 , а два оставшихся определяются смешанными
производными
, а два оставшихся определяются смешанными
производными 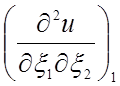 и
и 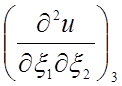 .
.
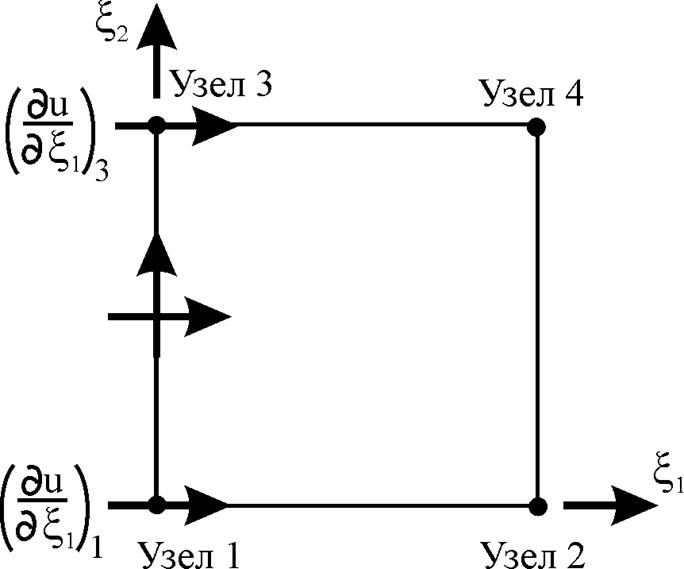
Рис.
13. Интерполяция узловой производной 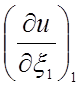 вдоль стороны 1-3
вдоль стороны 1-3
Интерполяция этих узловых параметров представляется следующим выражением:
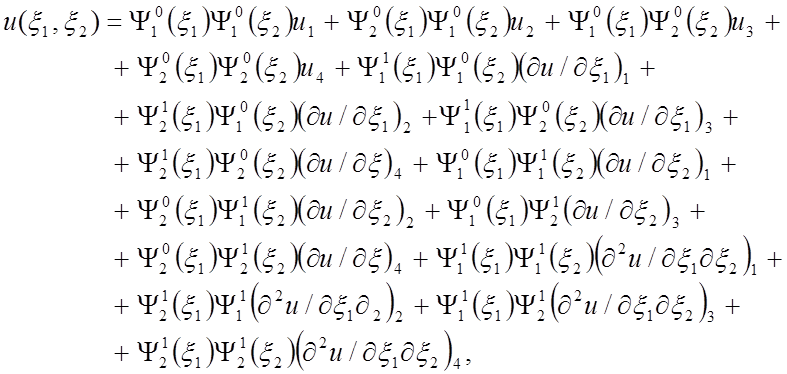 (27)
(27)
где функции ![]() описываются уравнениями (24).
описываются уравнениями (24).
Как и в
рассмотренном выше одномерном случае для сохранения непрерывности производной в
физическом пространстве x-координаты
и пространстве ![]() -координаты производные в
глобальные узлах должны быть определены относительно физического расстояния.
Рассмотрим две переменных: величину S1,
которая определяет расстояние вдоль направления x1, и величину S2, характеризующую расстояние по
направлению x2.
-координаты производные в
глобальные узлах должны быть определены относительно физического расстояния.
Рассмотрим две переменных: величину S1,
которая определяет расстояние вдоль направления x1, и величину S2, характеризующую расстояние по
направлению x2.
Тогда
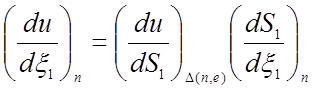 ,
,
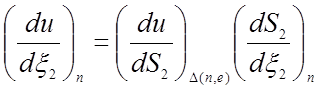 , (28)
, (28)
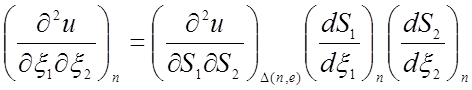 ,
,
где производные 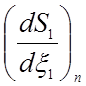 и
и 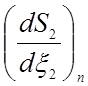 характеризуют
масштабные коэффициенты элементов, которые задают масштаб производных в
глобальном узле
характеризуют
масштабные коэффициенты элементов, которые задают масштаб производных в
глобальном узле ![]() по S координате относительно производной по x в узле n.
по S координате относительно производной по x в узле n.
Описанный выше бикубический базис Эрмита является мощным инструментом для описания криволинейных поверхностей. На рис. 14 приведена четырехэлементная бикубическая поверхность Эрмита в трехмерном пространстве, в котором каждый узел имеет следующие двенадцать параметров:
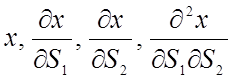 ,
,
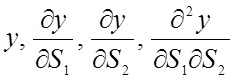 , (29)
, (29)
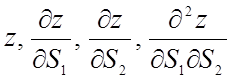 .
.
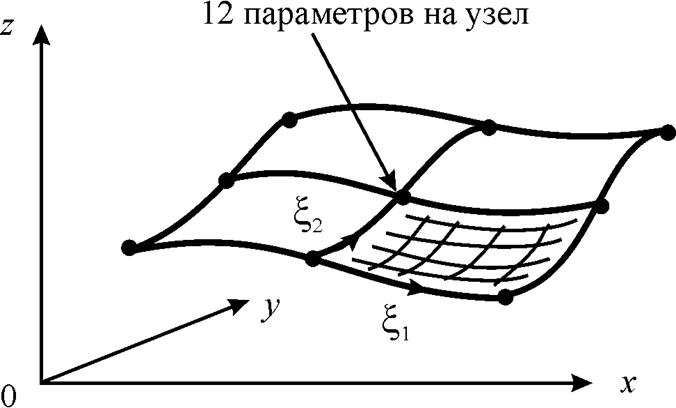
Рис.14. Поверхность, образованная бикубическими элементами Эрмита
Треугольные элементы
Треугольные элементы не могут использовать определенные выше координаты x1 и x2 для тензорного произведения элементов (т.е. двумерных и трехмерных элементов, базисные функции которых образованы произведением одномерных базисных функций). Координаты для треугольных элементов формируются на основе отношения площадей и называются координатами площади.
Рассмотрим отношение площади, образованной точками 2, 3 и P(x,y) на рис.15 к общей площади треугольника.
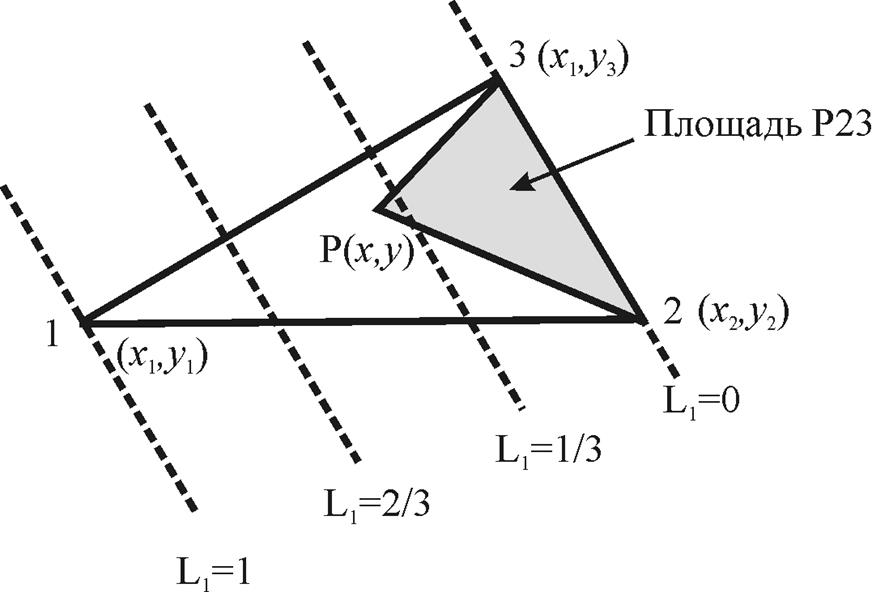
Рис. 15. Координаты площади треугольного элемента
Имеем
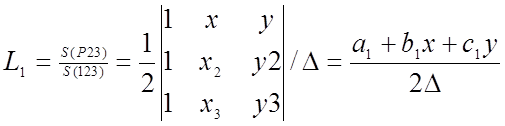 ,
,
где S(P23) и S(123) площади треугольников (P23) и (123) соответственно, а величина
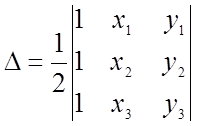
определяет площадь треугольника (123):
![]() ;
;
![]() ;
;
![]() .
.
Можно видеть, что величина L1 линейно зависит от координат x и y.
Для двух других треугольников, содержащих точку Р и две вершины элемента
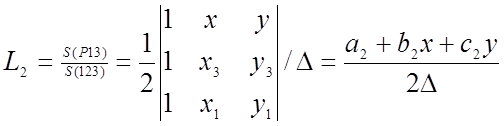 ,
,
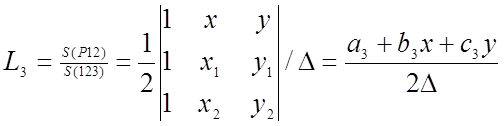 ,
,
где
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]() .
.
Заметим, что L1 + L2 + L3 = 1.
Величина L1 линейно изменяется от нуля (когда точка Р лежит на стороне 2-3) до 1 (точка Р совпадает с узлом 1) и поэтому может быть использована как базисная функция узла 1 для треугольника с четырьмя узлами.
Таким образом, интерполяция для треугольного элемента будет иметь вид:
![]() ,
,
где
![]() .
.
На рис. 16 показан квадратичный треугольный элемент, содержащий шесть узлов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
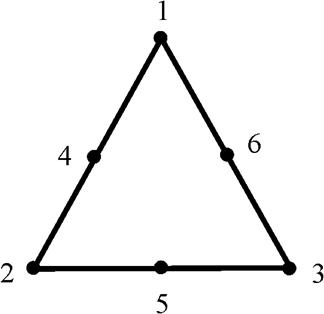
Рис. 16. Квадратичный треугольный элемент с шестью узлами
Библиографический список
1. Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.:Мир, 1986. 318 с.
2. Декланд Ж. Метод конечных элементов. М.:Мир, 1976. 316 с.
3. Сьярке Ф. Метод конечных элементов для эллиптических задач. М.:Мир, 1980. 296 с.
4. Самарский А.А. Введение в численные методы. М.:Наука, 1987. 286 с.
5. Калиткин Н.Н. Численные методы. М.:Наука, 1978. 512 с.
6. Вербжицкий В.М. Основы численных методов. М.: Высш.шк, 2002. 840 с.
7. Шуп Т.Е. Прикладные численные методы в физике и технике. М.: Высш.шк, 1990. 254 с.
Оглавление
Построение базисных функций ………………….…….………………. 1
Одномерное поле ……………………………………..………………… 1
Линейные базисные функции …………………………………....….… 2
Базисные функции как весовые функции …………….……….....….… 5
Квадратичные базисные функции …………..………….……………… 7
Двумерные и трехмерные элементы ……..………….………………… 8
Структуры высших порядков ……………………….………………… 12
Треугольные элементы ……………………..……….….……………… 19
Библиографический список ………………..…….….………………… 23
Филиппов Игорь Владимирович
Чернова Елена Владимировна
Подписано в печать 29.07.05. Формат бумаги 60´84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 1,5.
Уч.-изд. л. 1,5. Тираж 25 экз. Заказ
Рязанская государственная радиотехническая академия.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
ã Рязанская государственная
радиотехническая академия, 2005
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.