9 методах нулевого гюрядка используются лишь значения целе-нсД функции, в "летодах первого порядка, используются первые производные целевой (Тункиии или вектор градиента. Методы второго порядка используют вторые производные (матрицу Гессе) пелевой Функция, и их применение в задачах параметрического синтеза кон-птруто''^ весьма ограничено из-за трудностей вычисления вторых производных.
Исследуемые в работе метоц-i покоординатного спуска и сопря-"еччых нап^а-члений относятся к методам нулевого порядка..
2.2. !;1етод покоординатного спуска
|'ЛПС является простейшим методом нулевого порядка. Здесь в качестве векторов Sк направлений поиска последовательно вы-бяраятся направления, совпадающие с осями координат. Длина шага
»к обычно выбирается так, чтобы в выбранном направлении S^ целевая функция F(U) поднимала минимальное значение, .т.е. двоение в направлении S^ идет до тех пор, пока целевая функция продолжает убывать в данном направлении. При атом для выбора шага Т« используется один из методов однопараметрической оптимизации (дихотомического деления, Фибоначчи, "золотого сечения", квадратичной Интерпол™.™ и т.п.) [2,3,5].
Геометрическая интерпретация ?.'1ГЮ приведена на рис.1, где изображены личин равных значений F(U) =R= COnst целевой функ— w\ таух переменных и траектория вдпкения изображающей точки из начальной точки поиска И0 к оптимальной U " .
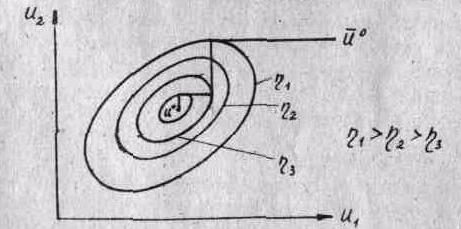
T^c.I
Яедостатком этого метода является его плохая с:сод:П!остъ для случая, когда поверхнооть целевой фунши!!! л^.ее" харакгер оврагов или гребней (рис.2). Здес'- в процессе поиска движение изображающей точки будет происходить с огг.юго склона oa; '.гз на другой о очень медленным продзи!&эн::е.1; к точке мщшмума. Кроме того, в данном методе поиск обычно прекра-цадтоя, есля веяичича шага Ук оказывается меньше некотороР. маштмалъноЁ величк!):-< Vmin ' ^ э?ом возможно прекращенпа почска вдали от канПпу^з. Так, например, на рис.2,б поиск г,'о,-'.ет быть пра:;ращен в ww. P , поскольку ни на одном из четырех направлен::? поиска при аеличинй шага У^-fmw нет ни одной точки, в KOTopoi! значение целевой функции убывает.
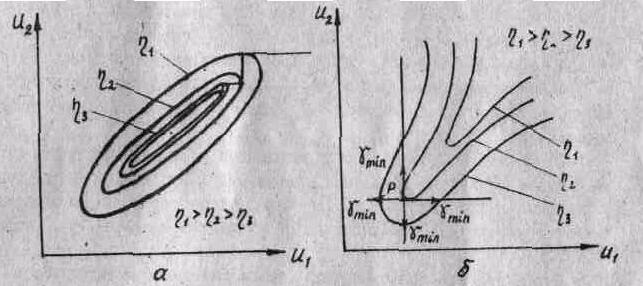
Рис. 2
Отметим, что наличие оаракных или греб.чевих оитуаци.3. (которое весьма характерно для задач', параметрического синтеза) имеет место при плохой обусловленности матрицн Гессе вторых частных производных целевой функции в. окрестное та экст),о"ально!"1 точки, т.е. если велико отно'иеЕ;яе наибольшего собственного значения данной матрицы к ее наименьшему значению.
2.3. Метод сопряженных направлений
Одни'л из наиболее эф^ектизныХ методов поиска нулевого г.орпц-ка является MG.4, который л'лшен большинства недостатков, iiiiinyui,nx MIE. Основным его преимуществом является в^юкая скорость cxoni!-мости. В частности, при минимизации положительно опрецелячной квадратичной форлы П . перер/ечны;'- o;i позцоляет найти ,^ичи,;'у'. не билее чем за п итераций. Так к:-г; чнсая гладкая гуннам и r)KT'e--:r-ности своего чинимума достаточ.ю х.).„-)11Ю.а.11;'ютоа:'!!!;,.уогод кнадг»0-тичной функцией, то метод ...1'J'i tyi':,ir ,:i.) прн/б.-мется ': для .vil^T'.m-ции яеквадратичных '{уикциЛ. i
Квадратичная форма Q представляет собой однородное выра-
яение второй степени от п переменных
а^и^й, (б)
где /4 - симметричная маврнпа, индекс Т означает символ транспонирования. Например, выражение
0. = а1, + ча^ + sa^ + чи,^ +2и^ +su_,u,
можно записать в виде (5), где
1^ 121
U= ^ , /1= 244
Us 145
Квадратичная форма О. является положительно определенной, "ели 0.^ О для всех U , а равенство имеет место лишь при U =0. Например, Q. = uf + 2.U^ +SU^ - положительно определенная форма, а Q = Uf + U^ + U^U^ не являетоя таковой.
Еоли квадратичная форма Q - положительно определенная, то соответствующая ей матрица А также называется положительно определенной.
С понятием положительно определенной,квадратичной формы тесно ^вязано понятие сопряженных направлений. Два направления, определяемые векторами X и у , называются сопряженными относительно симметричной положительно определенной матрицы А , если
УАи =о.
Сопряженность- можно считать обобщением Понятия-ортогональности. Действительно, если А = £ (где Е - единичная матри-па), то
X^U = у^^ = хг^ = °>
т.е. векторы х -я и ортогональны.
Важны?.. свойством сопряженных направлений, позволяющим эффект тивсо использовать та для решения задачи минимизапии, является слпэдячее свойотяо ^3,4J , которое мы приведем без доказательств за. • . .
' ftycTb •i;anEt4?? квадратячная функпия вида.
F(й)^^+^тй+^йrAй , (5)
где ' п - симметричная полркштельно определенная матрица и п , ^•-со!з™?ечи"х пг»п1;ар.7":г.1й S^, ^ц,,.., Од _ Тогда^провоэд ?лини-.у.^эглшй но : •'w'i эз н^равленик S' , 5д,...,-^п , можно по-.V-tnb ' wv.-л U'1 .--лнимума Функоии F(U) .
Т^з.ггш"'? "р.ч-^.яклипй тетодор сопряженных направлечи!"; otaii-
чавтся в основном способом построения втих направлр .'Л. Рассмотрим одну из таких модкфикапий, основанную на сде^ -кдах теопенах [З].
теорема I. 'Если при началыюй точке U0 поиска, р наипаиле-нии S миниглум квадратичной функияи (6) находятця в некоторой точке 1/" •и если при начальной точке поиска U.\ ^ И0 в том ке самом направлении S минимум находится в точке Us ,' то при F(йs)< F(U'1') направление U.s - U0' сопряжено с направлением S .
Основанная на этой теореме процедура поотросняя сопряженчо-го направления для двумерного случая иллюстрируется на ряо.3.

Рио.3
Эта теорема может быть распространена на отучай нппко.льких сопряженных направлений.
Теорема 2. Взли, начиная от точки И0 , точка U^ получается после_ использования ^ сопряженных иаправленчй ( Г <п ), а точка U. получается из точки U1 ф U.0 \}\w испочьзовачгти тех же сопряженных направлений и функция Р(U.) минимизируется на каждом из этих направлений, то вектор йs - U.0' сопряжен со всеми л направлениями.
Эти теоремы лежат в оонове опиоыр^еглого ни;ъ5 д„тт'01)".т.'да оо;.1;;:;-женных направлений.
Каждая итерация этого атгогятаа r,ouTo;i'i' из П +1 ^га, на каждом из которых осуществляется мяпиг/^заг^и \v\wh одного [тз направлений пояска. _ _ _ '
I^QTb U'o" - начатьчая точка ио1;кч, •л S^\ ^,..., S^- оо-вокупгюоть П напраяте.чи!'; пвиска. ''нача'1г1 и качестве чтпх мап-равлеяий так же, как ii в методе покоординатного спуска, вий^рем п направлений, рпвпацаы^их с вс^юи координат.
Лоэьмр'?1! з качестве исходного направления поиска направление п -и координатной оси S ^ и осуществим минимизацию функции в этом напра1элеч'га. Пусть при этом мн попадем в точку U^0',
OcyiiecTBtw теперь, начиная из точки U^°' , серию минимизаций и пероге^енпй w всех /7 направлениях поиска в следующей пс ледозательнооти: S'01, S^°\.... -S^, в результате мы попадем в некоторую точку й^ _; Нетрудно понять, что в силу теоремы I направления 5м и U-'^-U.^ сопряженные..
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.