Изучение методов получения и декодирования помехоустойчивых CRC-кодов, схем, реализующих эти методы

Цель работы

Изучение методов получения и декодирования помехоустойчивых CRC-кодов, схем, реализующих эти методы, и исследование эффективности простейшего CRC-кода (7,4) с образующим полиномом .

Теоретическая часть

CRC-коды (Cyclical Redundancy Check - циклический избыточный контроль) – помехоустойчивые избыточные коды с циклическими проверками, известные также как циклические коды. Они относятся к систематическим (n,k)-кодам, в которых информационные и проверочные символы располагаются на строго определенных позициях: информационные занимают k старших разрядов n–разрядной комбинации, проверочные – m=n-k младших разрядов. Особенностью CRC-кодов является то, что циклический сдвиг разрешенной комбинации, при котором старший разряд занимает место освободившегося младшего, приводит к другой разрешенной комбинации. Это и определяет название кодов. Благодаря хорошим корректирующим свойствам, относительно малой избыточности, простоте схемной реализации устройств кодирования и декодирования CRC-коды получили широкое распространение [1-3].

При описании CRC-кодов n–разрядные кодовые комбинации представляются в виде полиномов переменной x:

 ,

где  – коэффициенты, принимающие значение -х разрядов кодовой комбинации. Например, семиразрядной кодовой комбинации  соответствует полином .

                                             Таблица 1

m
1
2
3
4

Над полиномами, описывающими двоичные кодовые комбинации, можно выполнять все алгебраические операции, причем коэффициенты при одинаковых степенях переменной x складываются по модулю два (без переноса в старший разряд), а операция вычитания эквивалентна сложению.

 Основным свойством CRC-кодов является то, что все полиномы , представляющие кодовые комбинации CRC-кода (разрешенные комбинации), делятся без остатка на полином  степени m, который  называется образующим или производящим полиномом. Степень полинома  равна числу проверочных символов m=n-k. В качестве  используются неприводимые полиномы, т.е. такие, которые делятся без остатка только на единицу и на себя. Неприводимые полиномы играют роль, сходную с простыми числами в теории чисел. Вид неприводимого полинома зависит от числа проверочных символов m. Имеются таблицы неприводимых полиномов, некоторые  из которых представлены в табл. 1.

 Свойства делимости комбинации CRC-кода на образующий полином положено в основу циклического кодирования и декодирования.

Кодирование

Под кодированием понимается преобразование безызбыточной k-разрядной комбинации в n-разрядную комбинацию CRC-кода.

На практике широко используется кодирование по методу деления на образующий полином, согласно которому выполняются следующие операции.

1.  Подлежащая кодированию безызбыточная k-разрядная кодовая комбинация описывается полиномом C_k(x).

2.  Полином C_k(x)  умножается на x^m, что эквивалентно сдвигу безызбыточной k-разрядной комбинации влево (в сторону старших разрядов) на m разрядов или добавлению m нулей справа.

3.  Полученный полином C_k(x)x^m делится на образующий полином G_m(x), имеющий степень, равную числу проверочных символов m, в результате чего получаются целая часть Q(x) и остаток от деления  R(x):

,

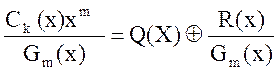 где  – знак суммирования по модулю два.

4.  Формируется n-разрядная разрешенная  комбинация    CRC-кода, соответствующая полиному:

,

для чего в освободившиеся при сдвиге разряды записывается комбинация, соответствующая остатку R(x).

Построим кодовую комбинацию CRC-кода (7,4), соответствующую безызбыточной комбинации 1001.

Общая длина комбинации n=7, число информационных символов k=4, проверочных – m=n–k=3. По таблице неприводимых полиномов табл.1 для  m=3 выберем образующий полином . В соответствии с рассмотренным методом кодирования получаем:

1.  

2.

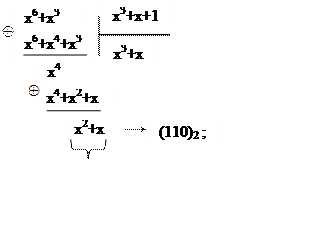3.   

4.

Все указанные операции можно выполнять непосредственно над кодовыми комбинациями.

Схема кодирующего устройства (КУ), реализующего рассмотренный метод кодирования, приведена на рис.1.

Рис.1. Схема кодирующего устройства

Кодирующее устройство представляет собой сдвиговый регистр с обратными связями через сумматоры по модулю два и строится по виду образующего полинома:

 ,

где   ,

m - число триггеров  в регистре.

Связи  и соответствующие им сумматоры присутствуют в схеме там, где .

Кодирование сводится к формированию в регистре m проверочных символов.

Перед началом кодирования триггеры  – в нулевом состоянии, ключ k1 – в положении «1», k2 – замкнут. Кодируемая безызбыточная k-разрядная комбинация поступает символ за символом в схему и одновременно через ключ k1 на выход КУ. Первым в этой последовательности идет символ старшего разряда. С приходом последнего k-го информационного символа формирование проверочных символов в КУ заканчивается, ключ k1 размыкается, ключ k2 переключается в положении «2» и сформированные в регистре проверочные символы поступают на выход вслед за информационными, что обеспечивается путем последовательного сдвига сформированной в регистре комбинации проверочных символов.

Декодирование

1. Обнаружение ошибок

Процедура обнаружения ошибки сводится к делению принятой комбинации на образующий полином  и принятию решения по виду остатка от деления .

Если остаток , то ошибки нет либо произошла необнаруживаемая кодом ошибка.

Если , то имеет место прием с ошибкой.

Декодирующее устройство (ДКУ) для обнаружения ошибок представляет собой схему деления на образующий полином. Такой схемой является сдвиговый регистр, охваченный обратными связями через сумматоры по модулю два (рис.2).

 

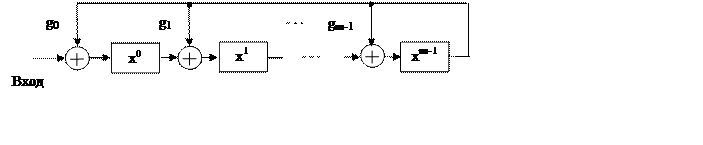Рис.2 Схема декодирующего устройства для обнаружения ошибок

Схема строится по виду образующего полинома . В схеме, построенной по конкретному образующему полиному, обратные связи и сумматоры отсутствуют там, где коэффициенты образующего полинома.

Принимаемая n-разрядная кодовая комбинация символ за символом вводится в регистр. В течение первых m тактов обратная связь не действует, так как триггер  – в нулевом состоянии. В течение последующих k=n-m тактов происходит деление: делимое суммируется по модулю два с делителем, поступающим через обратные связи. С поступлением последнего символа деление завершается. К этому моменту в регистре записан остаток, по виду которого принимается решение о наличии ошибки.

2. Исправление однократных ошибок

Определение  места  ошибки   в  принятой  комбинации   CRC-кода производится по виду остатка  от деления полинома  принятой комбинации на образующий полином.

Принятую с ошибкой в i-м разряде n-разрядную кодовую комбинацию CRC-кода можно представить полиномом:

 ,

где  – номер искаженного разряда, отсчитываемый от старшего; V_n(x) – полином комбинации CRC-кода, принятой без ошибки;  – полином однократной ошибки (ошибку можно представить как n–разрядную комбинацию с «1» в i-м разряде; например, при i=2 и n=5 ошибка представляется комбинацией 01000, которой соответствует полином x³).

После деления  на  получим:

.

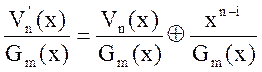Согласно свойству CRC-кода  делится на  без остатка. Следовательно, остаток от деления  равен остатку от деления , т.е. не зависит от вида , а определяется только положением принятого с ошибкой символа. Это позволяет определить место ошибки путем последовательных сдвигов принимаемой комбинации в сторону старшего разряда и сравнения остатков  (-число сдвигов) от деления сдвигаемой комбинации с остатком  (выделенным синдромом) от деления полинома , описывающего ошибку в старшем разряде. При совпадении остатков  принимается решение об искажении символа , номер которого на единицу больше числа сдвигов  [2,3].