5. Диффузное рассеяние рентгеновских лучей
под малыми углами макромолекулами в растворе
Как
следует из заголовка, этот метод позволяет изучать макромолекулы в растворе, то
есть в условиях, приближенных к естественным. Так как образец не является
кристаллом, то информация, получаемая в этом случае, будет ограниченной. Из
эксперимента можно определять радиус инерции распределения электронной
плотности макромолекулы и в некоторых случаях ее молекулярную массу. (Радиусом
инерции называется величина ![]() , имеющая
размерность длины, с помощью которой момент инерции тела (
, имеющая
размерность длины, с помощью которой момент инерции тела (![]() ) относительно данной оси выражается
формулой
) относительно данной оси выражается
формулой ![]() , где
, где ![]() –
масса тела. Например, для однородного шара радиус инерции относительно оси,
проходящей через его центр, равен
–
масса тела. Например, для однородного шара радиус инерции относительно оси,
проходящей через его центр, равен ![]() , где
, где ![]() – радиус шара.) Можно отметить, что
радиус инерции не позволяет определить формы молекулы. Поэтому для ее установления
необходимо рассчитывать рассеяние от различных моделей и сравнивать полученные
теоретические кривые с экспериментальными.
– радиус шара.) Можно отметить, что
радиус инерции не позволяет определить формы молекулы. Поэтому для ее установления
необходимо рассчитывать рассеяние от различных моделей и сравнивать полученные
теоретические кривые с экспериментальными.
Пусть объект содержит большое число частиц, ориентированных произвольным образом. Считаем также, что объем, приходящийся на каждую частицу, значительно больше объема частицы. Тогда волны, рассеянные такими частицами, не будут интерферировать, а регистрируемая интенсивность определяется средней интенсивностью дифракции на частице с учетом всех возможных ее ориентировок.
В
случае частиц, находящихся в растворе, имеющем электронную плотность ![]() , интенсивность рассеяния одной
частицей определяется следующим выражением:
, интенсивность рассеяния одной
частицей определяется следующим выражением:
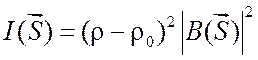 ,
(5.1)
,
(5.1)
где ![]() – трансформанта Фурье фактора формы
частицы
– трансформанта Фурье фактора формы
частицы ![]() , то есть функции, которая равна
единице внутри частицы и нулю – вне частицы:
, то есть функции, которая равна
единице внутри частицы и нулю – вне частицы:
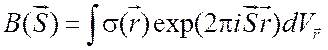 . (5.2)
. (5.2)
Таким
образом, объект можно рассматривать как суперпозицию частиц с плотностью ![]() и среды постоянной плотности
и среды постоянной плотности ![]() .
.
Для
произвольной ориентации частиц зависимость интенсивности рассеяния одной
частицей от величины 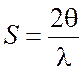 выражается через среднее
значение
выражается через среднее
значение 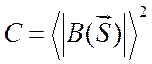 на сфере радиусом
на сфере радиусом 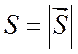 :
:
![]() . (5.3)
. (5.3)
Следовательно
расчет рентгенограмм от однородных частиц данной формы осуществляется с помощью
выражений (5.1) и (5.3). Такие расчеты ![]() выполнены
для частиц различной формы. Мы в качестве примера рассмотрим рассеяние
сферическими частицами. В этом случае трансформанта
выполнены
для частиц различной формы. Мы в качестве примера рассмотрим рассеяние
сферическими частицами. В этом случае трансформанта ![]() имеет
вид:
имеет
вид:
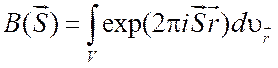 , (5.4)
, (5.4)
где
интеграл берется по объему ![]() сферы радиусом
сферы радиусом ![]() . Можно показать, что он равен
. Можно показать, что он равен
 . (5.5)
. (5.5)
Учитывая выражение (5.3), находим рассеивающую способность одной частицы
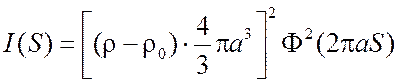 . (5.6)
. (5.6)
Примерный график этой зависимости представлен на рис. 5.1.
|
|
Рис. 5.1. График интенсивности рассеяния от
однородной сферы радиусом а 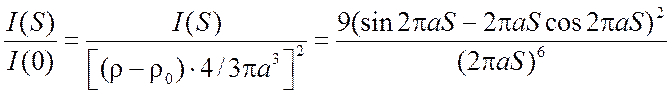 . Пунктиром для
сравнения показана асимптотическая функция
. Пунктиром для
сравнения показана асимптотическая функция 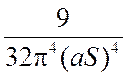 ,
которая применима для зерен произвольной формы, полностью дезориентированных и
не имеющих нулевых размеров в каком-либо направлении (например, не плоский диск
и не палочка)
,
которая применима для зерен произвольной формы, полностью дезориентированных и
не имеющих нулевых размеров в каком-либо направлении (например, не плоский диск
и не палочка)
Таким образом, на рентгенограмме будет наблюдаться центральное пятно, окруженное кольцами с уменьшающейся интенсивностью. Действительно, снимок такого вида можно регистрировать от образца латекса, состоящего из сфер одинакового диаметра, взвешенных в воде. Установлено, что приближенное выражение рассеивающей способности одной частицы произвольной формы имеет вид
![]() , (5.7) где
, (5.7) где ![]() – полное число электронов в частице,
а
– полное число электронов в частице,
а ![]() – средний радиус инерции,
соответствующий направлению
– средний радиус инерции,
соответствующий направлению ![]() .
.
В
случае сферической частицы радиусом ![]() радиус инерции не
зависит от направления
радиус инерции не
зависит от направления ![]() . Тогда приближенное
выражение формулы (5.6) примет вид для центрального пятна рассеяния
. Тогда приближенное
выражение формулы (5.6) примет вид для центрального пятна рассеяния
 . (5.8)
. (5.8)
Приближенное выражение (5.8) достаточно хорошо совпадает с точным выражением (5.6), что показано на рис. 5.2.
|
|
Рис. 5.2. Сравнение интенсивностей рассеяния на сфере, рассчитанных по точной (а) и приближенной экспоненциальной (б) формулам
Рассмотрим случай частиц произвольной формы, но одинаково ориентированных.
Тогда формула (5.7) позволяет определить вид диффузного пятна. В этом случае
пятно будет более вытянутым в плоскости наблюдения, перпендикулярной к первичному
пучку, в том направлении, в котором величина ![]() будет
наименьшей. На рис. 5.3 показан случай дифракции на эллипсоиде вращения,
который подтверждает сказанное выше.
будет
наименьшей. На рис. 5.3 показан случай дифракции на эллипсоиде вращения,
который подтверждает сказанное выше.
|
|
Рис. 5.3. Диффузное рассеяние под малыми углами на
эллипсоиде вращения с главной осью, перпендикулярной к первичному рентгеновскому пучку
Если частицы ориентированы произвольно, то
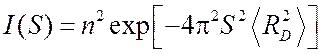 , (5.9)
, (5.9)
где 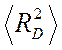 – среднее значение
– среднее значение ![]() , взятое по всем направлениям
, взятое по всем направлениям ![]() . Радиус инерции частицы
. Радиус инерции частицы ![]() можно выразить через среднее значение
(
можно выразить через среднее значение
(![]() ) радиусов инерции по отношению к
трем координатным плоскостям:
) радиусов инерции по отношению к
трем координатным плоскостям:
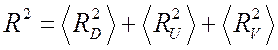 .
(5.10)
.
(5.10)
Если
произвольно изменять направления, то 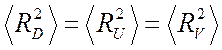 , а
, а ![]() не будет изменяться. Тогда
не будет изменяться. Тогда 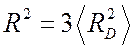 . Следовательно, для рассеивающей способности
одной частицы в этом случае, для угла рассеяния
. Следовательно, для рассеивающей способности
одной частицы в этом случае, для угла рассеяния ![]() ,
имеем
,
имеем
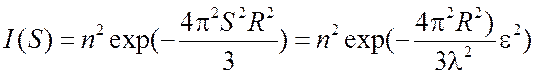 . (5.11)
. (5.11)
Можно
показать, что выражение (5.11) справедливо и для общего случая неоднородных
частиц, то есть частиц, состоящих из разных сортов атомов. Чтобы найти
интенсивность рассеянного излучения от ![]() частиц,
нужно выражение (5.11) умножить на
частиц,
нужно выражение (5.11) умножить на ![]() .
.
Логарифмируя выражение (5.11), получаем
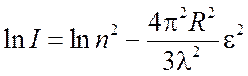 . (5.12)
. (5.12)
Поэтому зависимость ![]() от
от
![]() при малых значениях
при малых значениях ![]() является прямой, по наклону которой
является прямой, по наклону которой 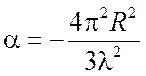 можно определить радиус инерции
можно определить радиус инерции
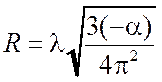 .
(5.13)
.
(5.13)
Используемая аппаратура определяет некоторый предельный угол ![]() . При достаточно малом радиусе
инерции частиц этот угол будет меньше угла, для которого справедливо
экспоненциальное приближение; тогда формула (5.13) позволяет определить радиус
инерции частицы. Подчеркнем еще раз, что метод основан на измерении наклона
прямой при малых значениях
. При достаточно малом радиусе
инерции частиц этот угол будет меньше угла, для которого справедливо
экспоненциальное приближение; тогда формула (5.13) позволяет определить радиус
инерции частицы. Подчеркнем еще раз, что метод основан на измерении наклона
прямой при малых значениях ![]() , то есть вблизи
первичного пучка. Укажем, что для
, то есть вблизи
первичного пучка. Укажем, что для 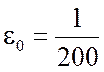 и
и ![]() Å верхний предел радиуса инерции,
который еще можно определить, равен 60 Å для сфер и 35 Å для сильно вытянутых
цилиндров.
Å верхний предел радиуса инерции,
который еще можно определить, равен 60 Å для сфер и 35 Å для сильно вытянутых
цилиндров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.