Расчет эластичности расходов предприятия для двух видов продукции. Расчет значимости коэффициентов

ФГОУ ВПО Вятская государственная сельскохозяйственная

 академия

Экономический факультет

Личное дело 05118/ф                  Оценка_________________________

Регистрационный номер в деканате___________________________

Работа поступила в деканат «____»_____________________2008г.

КОНТРОЛЬНАЯ РАБОТА № 1

По предмету    Эконометрика

На тему___________________________________________________

Специальность Финансы и кредит

Студента 5 курса экономического факультета платной заочной, заочной ускоренной формы обучения

Выполнил                   Земцов Эдуард Николаевич

Набор                октябрь 2005г.

Преподаватель Сысолятина Ирина Владимировна

Регистрационный № на кафедре______________________________

Работа поступила на кафедру «___»_____________________2008г.

Задача №1.

Для двух видов продукции А и Б зависимость расходов предприятия y (тыс. руб.) от объема производства x (шт.) характеризуется данными, представленными в таблице:

Уравнение регрессии	Показатели корреляции	Число наблюдений
yА = 160 + 0,8x	0,85	30
yБ = 50x0,6	0,72	25

1. Величины 0,8 и 0,6 – коэффициенты регрессии.

Коэффициент регрессии показывает среднее изменение результата y с изменением фактора x на одну единицу. Т.е. если объем производства продукции А увеличится на 1 шт., то это приведет к увеличению расходов предприятия на 800 руб. Соответственно, расходы предприятия при производстве продукции Б растут прямо пропорционально 0,6 степени роста объема производства.

2. Найдем эластичность расходов предприятия при производстве продукции А и Б:

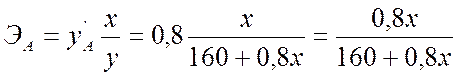
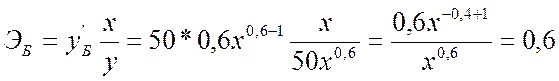
Мы видим, что эластичность расходов предприятия при производстве продукции Б постоянна и составляет 0,6, т.е. при изменении объема производства продукции Б на 1% расходы увеличиваются в среднем на 0,6%.

Найдем эластичность расходов предприятия при производстве продукции А в объеме 500 шт.:

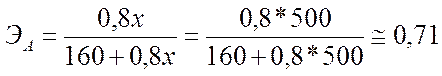
Таким образом, при производстве продукции А в объеме 500 шт. эластичность расходов больше, чем при при производстве продукции Б, т.е. производство продукции А в таком объеме ведет к увеличению расходов предприятия, чем производство продукции Б.

3. Чтобы вычислить, при каком уровне производства продукции А эластичность расходов предприятия будет равна эластичности расходов производства продукции Б, необходимо выполнить условие Э_А = Э_Б:

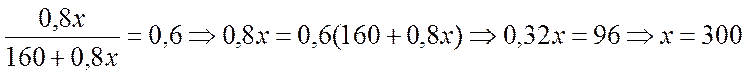
Т.е. при уровне производства продукции А в 300 шт. эластичность ее расходов будет равна эластичности расходов при производстве продукции Б.

4. F-критерий рассчитывается по формуле:

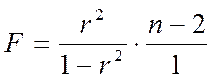
где     r – коэффициент корреляции,

n – количество наблюдений.

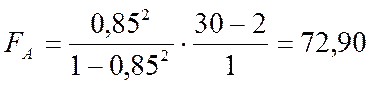
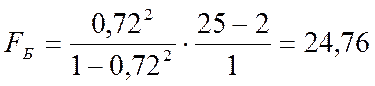
Оба значения F-критерия превышают табличные, поэтому оба уравнения регрессии являются значимыми.

Задача 2.

Известны данные по территории Уральского и Западно-Сибирского районов за ноябрь 1997 г.:

Территория	Потребительские расходы на душу населения, тыс. руб. (y)	Средняя з/п и выплаты социального характера, тыс. руб. (x)
Уральский
Респ. Башкортостан	461	912
Удмуртская респ.	524	809
Курганская обл.	298	748
Оренбургская обл.	351	847
Пермская обл.	624	1087
Свердловская обл.	584	1074
Челябинская обл.	425	1008
Западно-Сибирский
Респ. Алтай	277	682
Алтайский край	321	697
Кемеровская обл.	573	1251
Новосибирская обл.	576	967
Омская обл.	588	898
Томская обл.	497	1263
Тюменская обл.	863	3027

Рассчитаем параметры линейного, степенного и показательного уравнений парной регрессии.

Задача состоит в том, чтобы найти коэффициенты a и b уравнения в виде y = a + bx. Используя МНК и MS Excel, получаем y = 263,41 + 0,21x.

Оценка значимости уравнения регрессии дается с помощью коэффициента корреляции, детерминации и F-критерия. Коэффициент корреляции показывает, насколько тесно связаны между собой фактор х и результат y. Чем ближе его значение к 1, тем более явно одна переменная влияет на другую. Коэффициент корреляции равен r = 0,80, что говорит о связи между параметрами, но не слишком тесной. При этом коэффициент детерминации равен r² = 0,63, что свидетельствует в пользу значимости уравнения линейной регрессии. Критерий Фишера составил F = 20,60, что превышает табличное значение и подтверждает предположение о зависимости результативного признака от факторного. Таким образом, уравнение линейной регрессии статистически значимо.

Далее построим показательное уравнение для тех же данных в виде y = ab^х. Получаем y = 347,85 ∙ 1,0003^х.

r = 0,74

r² = 0,55

F = 15,93

Значения всех трех показателей хуже соответствующих для линейной модели, т.е. линейная модель лучше описывает реальную ситуацию. Коэффициент корреляции говорит о средней связи между факторным признаком и результативным. Коэффициент детерминации показывает, что всего 55% вариации результативного признака объясняется вариацией факторного, соответственно остальные 45% - остальными (случайными) факторами, которые не вошли в модель.

Если сравнивать две модели, то линейная функция больше подходит для моделирования данной ситуации.

Далее построим степенное уравнение для тех же данных в виде y = aх^b. Получаем y = 10,45х^0,56.

r = 0,90

r² = 0,82

F = 25,59

Полученное уравнение значимо, т.к. критерий Фишера намного превышает табличное значение, и лучше описывает реальную ситуацию. Коэффициент корреляции равен 0,90, что говорит о тесной связи между признаками и о сильном влиянии фактора х на результат y. Судя по коэффициенту детерминации 82% вариации результативного признака объясняется вариацией факторного и всего 18% - остальными факторами. Эти показатели лучше, чем для линейной модели, т.е. для моделирования данной ситуации наиболее целесообразно использовать именно степенную модель.

Задача 3.

По 50 семьям изучалось потребление мяса – y (кг на душу населения) от дохода – x₁ (руб. на одного члена семьи) и от потребления рыбы – x₂ (кг на душу населения). Результат y = – 180 + 0,2х₁ – 0,4х₂. Cтандартные ошибки соответственно равны 20; 0,01; 0,25. Множественный коэффициент корреляции 0,85.

1.  Коэффициент детерминации равен квадрату коэффициента корреляции 0,85² = 0,72.

2.  Рассчитаем критерий Стьюдента по формуле:

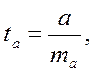
где     а – соответствующий параметр,

m^a – его стандартная ошибка.

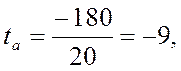
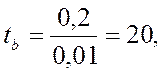
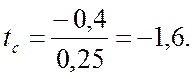
Значения первых двух критериев Стьюдента превышают табличные, соответственно коэффициенты а и b регрессии значимы. Коэффициент с не значим.

3. Рассчитаем частные F-критерии как квадраты соответствующих t-критериев: F_B = 400, F_C = 2,56. Таким образом, введение в модель фактора х₁ после фактора х₂ целесообразно, т.к. фактор х₁ лучше объясняет вариацию результативного признака. Введение в модель фактора х₂ после фактора х₁ целесообразно, т.к. фактор не оказывает сильного влияния на результат.