Основні характеристики систем комутації з очікуванням

Додаток В

ОСНОВНІ ХАРАКТЕРИСТИКИ СИСТЕМ КОМУТАЦІЇ З ОЧІКУВАННЯМ

Дисципліною обслуговування з очікуванням називається така, при якій заявка, що надходить у систему за відсутності вільних приладів (каналів), не втрачається, а ставиться до черги, очікуючи звільнення будь-якого з них.

Поряд із завантаженням каналів (див. Додаток Б) до показників якості  системи комутації з очікуванням входять наступні характеристики:

·  імовірність  умовних втрат за часом як середня частка часу, протягом якої всі канали системи, що доступні групі джерел заявок, зайняті обслуговуванням;

·  імовірність  очікування початку обслуговування заявкою понад заданого часу  як відношення середньої кількості затриманих понад час  заявок до середньої кількості, що надійшли;

·  середній час очікування  початку обслуговування;

·  імовірність  того, що довжина черги  перевищить задану величину ;

·  середня довжина черги .

При обчисленні цих характеристик використовуються імовірності станів системи комутації з очікуванням. Ці стани  визначаються кількістю заявок, які присутні у системі комутації:

·  стан , якщо система комутації вільна;

·  стан , якщо зайнятий один канал, а інші вільні;

·  стан , якщо зайнято і каналів з їх загального числа , а інші вільні;

·  стан , якщо зайняті всі каналів системи комутації;

·  стан , якщо зайняті всі  каналів системи комутації та одна заявка стоїть у черзі;

·  стан , якщо зайняті всі  каналів системи комутації та  заявок стоять у черзі.

Довжина черги буде кінцевою, якщо інтенсивність навантаження , що надходить, менша за кількість каналів .

У випадку найпростішого потоку заявок з параметром  і показниково розподіленої тривалості обслуговування з функцією .

Фінальні імовірності станів  визначаються формулами [1, 2]

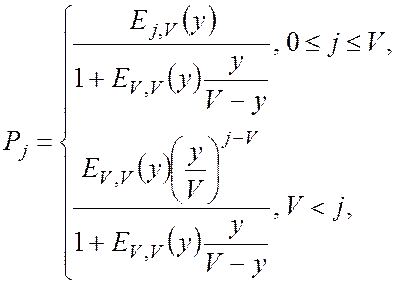                                   (В.1)

де  - відповідає першій формулі Ерланга (Б.4);

 - інтенсивність навантаження, що надходить.

З виразу (В.1) виходить, що для систем комутації з очікуванням час знаходження у станах, коли заявки негайно обслуговуються, менш ніж для систем з втратами.

Для систем комутації з очікуванням імовірність умовних втрат за часом – це середня частка часу, протягом якого всі  каналів зайняті обслуговуванням, а в черзі на очікуванні знаходиться  заявок. Тому вона співпадає з імовірністю того, що заявка не буде негайно обслуговуватись, а буде очікувати початку обслуговування протягом часу очікування більш нуля. Ця імовірність визначається як

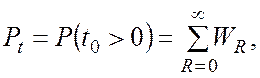                                            (В.2)

де  - розподіл довжини черги , який задається ймовірностями станів  та відповідно до (В.2) визначається виразом

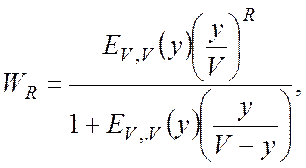                                     (В.3)

.

Використовуючи (В.2), (В.3), імовірності умовних втрат за часом можна записати у вигляді формули

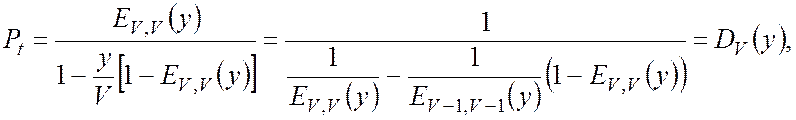          (В.4)

яка носить назву другої формули Ерланга.

Імовірність  очікування початку обслуговування понад заданого часу  у випадку найпростішого потоку заявок і показниково розподіленої тривалості обслуговування визначається як

                           (В.5)

а середній час очікування початку обслуговування

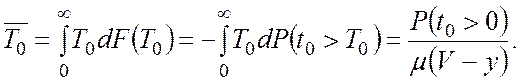                           (В.6)

Відповідні характеристики довжини черги позначаються виразами

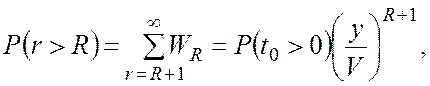                              (В.7)

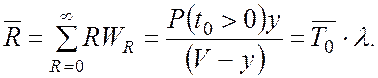.                                    (В.8)

Вираз (В.8) має назву формули Літла [2], що справедлива для будь-якої відкритої системи комутації з очікуванням, у якій параметр потоку заявок не залежить від її стану.

Динаміка станів систем комутації з очікуванням для найпростішого потоку заявок і показникові розподіленої тривалості обслуговування описується дискретним марківським процесом народження і загибелі [1]. Тому, для їх імітаційного статистичного моделювання у програмі TSS використовується ланцюг Маркова із -м станом  що створюється на інтервалі спостереження послідовністю відліків процесу народження і загибелі в моменти часу  У цих ланцюгах розглядаються наступні переходи між станами через одиничний інтервал часу:

·  з будь-якого стану   у три найближчі стани  з імовірностями  відповідно;

·  зі стану  у стани  та  з ймовірностями та  відповідно;

·  зі стану  у стани  та  з ймовірностями та  відповідно.

Для одиничного інтервалу модельного часу, який дорівнює, наприклад, 1 хвилині, імовірності переходів визначаються формулами

                                        (В.9)

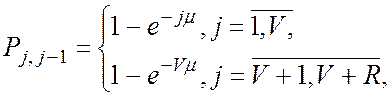                                   (В.10)

                          (В.11)

                                                     (В.12)

                                          (В.13)

У випадку найпростішого потоку заявок з параметром  і постійної тривалості обслуговування  динаміку станів систем комутації з очікуванням не можна описати дискретним марківським процесом народження і загибелі [1]. До цього процесу має відношення тільки її складова, що дозволяє при моделюванні використовувати формули (В.9), (В.11), (В.12) для ймовірностей переходів у вищі стани або збереження їх на межах. Процес обслуговування у цих умовах моделюється детермінованими переходами у нижчі стани після часу .

Аналітичні методи дослідження таких процесів обслуговування базуються на теорії Кромеліна [1, 2], яка дозволяє отримати вирази для фінальних ймовірностей станів одноканальної систем комутації з очікуванням [2]

,                                                      (В.14)

,                                      (В.15)

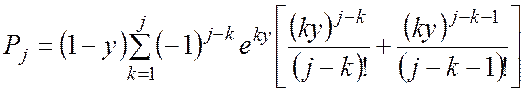, ,          (В.16)

де  - інтенсивність навантаження, що надходить.

У виразі (В.16) при  співмножник у квадратних дужках не враховується.

Ці вирази для ймовірностей станів дозволяють обчислювати наступні характеристики системи:

·  функцію розподілу часу очікування

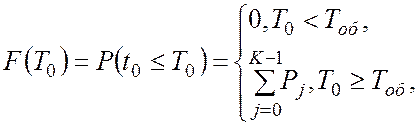                               (В.17)

де К- ціла частина дійсного числа

·  імовірність умовних втрат за часом

                                                     (В.18)

·  імовірність очікування початку обслуговування понад заданого часу

.                                             (В.19)

Середній час очікування початку обслуговування  можна обчислювати за формулою Полячека-Хінчіна [1, 2], яка у випадку постійної тривалості обслуговування має вигляд

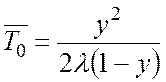.                                              (В.20)