Основні характеристики потоків заявок

Додаток А

ОСНОВНІ ХАРАКТЕРИСТИКИ ПОТОКІВ ЗАЯВОК

Мережа електричного зв'язку являє собою комплекс технічних засобів, призначених для передачі та розподілу інформації. Системи комутації призначені для рішень задачі розподілу інформації.

За принципом утворення трактів для передачі інформації мережі поділяються на мережі без вузлів комутації і з вузлами комутації. У першому випадку використовуються постійно діючі тракти між абонентськими пристроями. Абонентський пристрій у телефонії – це телефонний апарат, а в мережах передачі дискретних повідомлень – телеграф.

Виклики від абонентів мережі надходять на комутаційні станції по абонентських і з’єднувальних лініях. Послідовність викликів, що надходять на вузли комутації у деякі моменти часу, називаються потоком викликів (заявок).

Детермінований потік - це потік викликів з фіксованими моментами надходження заявок. Такий потік рідко зустрічається. Якщо моменти надходження викликів залежать від випадкових факторів, то потік називається випадковим. Випадковий потік заявок, як послідовність випадкових величин може бути заданий трьома еквівалентними засобами:

- послідовністю випадкових моментів часу появи заявок , ;

- послідовністю випадкових інтервалів часу між заявками , ;

- послідовністю випадкових чисел  ; що визначають кількість заявок на заданих інтервалах часу [t₀ , t_i ), .

При перших двох засобах завдання, потік заявок розглядається як випадковий точковий процес, а при третьому - як випадковий цілочисельний процес  із початковою умовою .

Імовірнісний опис цих випадкових процесів використовує наступні характеристики:

- спільну функцію розподілу моментів часу появи заявок  або відповідну їй щільність імовірності ;

- спільну функцію розподілу інтервалів часу між заявками  або відповідну їй щільність імовірності ;

- спільний закон розподілу кількості заявок на заданих інтервалах часу

Потік заявок є однорідним, якщо він повністю характеризується закономірністю надходження заявок у ньому, наприклад, ймовірнісними характеристиками моментів появи заявок або інтервалів між ними. У випадку неоднорідного потоку кожна заявка має дві або більше характеристики.

Потік заявок є стаціонарним, якщо спільний закон розподілу кількості заявок на заданих  інтервалах часу не залежить від початкового моменту часу . Фактично стаціонарність потоку означає, імовірність надходження деякої кількості заявок за фіксований інтервал часу залежить тільки від довжини інтервалу і не залежить від його початку. Потік, який не має цієї властивості, є нестаціонарним.

Потік заявок є ординарним, якщо для імовірності  надходження двох і більше заявок за інтервал часу  існує межа

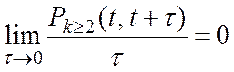.                                              (А.1)

Фактично ординарність означає неможливість одночасного надходження двох і більше заявок. Потік який не має цієї властивості є неординарним.

Потік заявок є потоком без післядії, якщо імовірність надходження заявок за інтервал часу  не залежить від процесу надходження заявок до моменту . Зокрема, відсутність післядії означає взаємну незалежність появи кількостей заявок на інтервалах часу, що не перекриваються. Потік, який не має цієї властивості, називається потоком з післядією.

Кількісне описання потоків заявок використовує три основні характеристики:

- провідну функцію потоку , що являє собою середню кількість заявок за інтервал часу ;

- інтенсивність потоку , що являє собою середню кількість заявок які надходять в одиницю часу

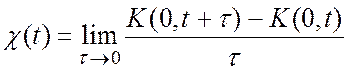;                              (А.2)

- параметр потоку

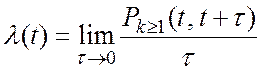;                                (А.З)

де  - ймовірність появи хоча б однієї заявки на інтервалі часу .

Потоки, що мають неперервну провідну функцію називаються регулярними, а ті, що мають східчасту провідну функцію – сингулярними.

У випадку стаціонарних потоків інтенсивність та параметр потоку не залежать від часу, при чому . Рівність цих характеристик має місце для ординарних потоків.

Однорідний стаціонарний ординарний потік без післядії називається найпростішим потоком. Інтервали часу між заявками в ньому є незалежними випадковими величинами з показниковим розподілом, для якого функція розподілу  та щільність розподілу  мають вигляд

,                                        (А.4)

.                                          (А.5)

Найпростіший потік також називається пуассонівським, бо кількість його заявок  на інтервалі часу тривалістю  розподілена за законом Пуассона

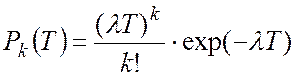,                                      (А.6)

де

Якщо розглядати найпростіший потік як цілочисельний випадковий процес, то вів може бути віднесений  до класу дискретних марківських  процесів чистого народження [1,2]. Тому для його імітаційного статистичного моделювання у програмі tss.exe застосовується ланцюг Маркова, що створюється на інтервалі спостереження послідовності N відліків дискретного за часом марківського процесу чистого народження: , , з номером  для початкового відліку та номером  для останнього відліку, а величина  має сенс кількості заявок на інтервалі .

При моделюванні припускається що початковий стан ланцюга , а в і-й момент для його стану можливі два варіанти:

- перехід до наступного стану   з імовірністю P;

- збереження попереднього стану  з імовірністю 1-Р.

Для одиничного інтервалу модельного часу, який дорівнює приміром, 1 хвилина імовірність обчислюється за формулою

,                                                    (А.7)

де  - параметр найпростішого потоку.

Нестаціонарним  пуассонівським потоком (найпростішим потоком із змінним параметром) є однорідний ординарний потік без післядії, параметр  якого залежить від часу t, а ймовірність появи точно k заявок на інтервалі часу  визначається формулою

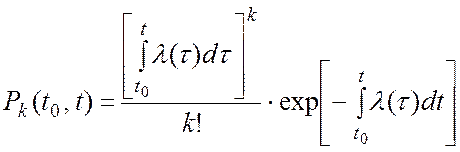,                        (А.8)

де

Неординарним пуассонівським потоком є однорідний стаціонарний потік без післядії, для якого імовірність появи точно k заявок на інтервалі тривалістю Т  визначається законом Пуассона, а кількість заявок у кожний момент часу їхньої появи визначається характеристикою неординарності .

Якщо характеристика неординарності є детермінованою величиною, то сумарна кількість заявок на інтервалі часу тривалістю  з імовірністю дорівнює  Якщо ж вона - випадкова величина, що означає надходження в кожний момент часу l заявок з імовірністю , то інтенсивність потоку

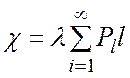.                                                   (А.9)

Під потоком з обмеженою післядією розуміється однорідний ординарний  потік заявок, у якого послідовність інтервалів часу між заявками   представляє послідовність незалежних випадкових величин, що мають будь-які функції розподілу. Такий потік викликів описується послідовністю функцій розподілу ,

Потік з обмеженою післядією називається рекурентним потоком або потоком Пальма, якщо всі функції розподілу , за винятком можливо , співпадають. Окремим випадком потоку Пальма є рекурентний потік відновлення, що характеризується всіма однаковими функціями розподілу. внаслідок однаковості розподілів для тривалостей інтервалів часу між заявками ці потоки завжди стаціонарні.

Прикладом рекурентних потоків відновлення є ерлангівські потоки, які формуються з найпростіших потоків внаслідок використання операції проріджування. Проріджування потоку являє собою вилучення частини заявок з нього із збереженням тих, що залишилися, у новому потоці який називається прорідженим.

Якщо до найпростішого потоку з параметром  застосувати операцію проріджування, при якій т заявок підряд втрачається, а залишається тільки кожна (т+1)-a, утвориться проріджений потік з параметром та щільністю імовірності для інтервалів часу між заявками

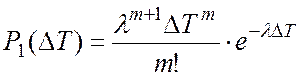 ,                                    (А.10)

де .

Розподіл з такою щільністю носить назву розподілу Ерланга m-го порядку. Цей розподіл можна розглядати як розподіл для тривалості інтервалів часу до появи m+1-ї заявки найпростішого потоку.

Перевагою розподілу Ерланга є можливість опису з його допомогою широкого класу потоків - від найпростіших з показниково розподіленими тривалостями інтервалів часу між заявками (при  у формулі (А.10)) до детермінованих з постійною тривалістю інтервалів часу між заявками (при  у формулі (А.10)).

З операції проріджування виходить, що для появи точно  заявок Ерлангівського потоку на інтервалі часу тривалістю  необхідна поява на ньому не менше  та не більше  заявок найпростішого потоку, що проріджується. Тому з правила додавання ймовірностей з урахуванням (А.6) для імовірності цієї події одержуємо формулу

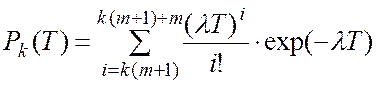.                          (А.11)

Формування Ерлангівського потоку за допомогою такого проріджування найпростішого потоку використовується у програмі tss і характерно для багатоканальних систем комутації, у яких вхідний найпростіший потік розділяється на  каналів таким чином, що перша заявка потоку надходить на обслуговування першим каналом, …, -а - -м каналом, -а знову потрапляє на обслуговування першим каналом и так далі.

Ще більша залежність від характеристик систем комутації властива потокам з простою післядією.

Під потоком з простою післядією розуміється однорідний ординарний потік, для якого у будь-який момент часу tіснує кінцевий параметр потоку , що залежить тільки від стану S(t) системи комутації в цей момент і не залежить від процесу обслуговування заявок до цього моменту. Потік з простою післядією є нестаціонарним, бо його параметр залежить від часу через стан системи, хоча для кожного конкретного стану цей параметр є постійною величиною.

До окремих випадків потоку з простою післядією відносяться симетричний  та примітивний потоки.

Симетричним називається потік з простою післядією, параметр  якого у будь-який момент часу t залежить тільки від кількості i заявок, що обслуговуються в цей момент, і не залежить від інших характеристик, які визначають стан S(t) системи. Таким чином, .

Примітивний називається такий симетричний потік, параметр якого  прямо пропорційний кількості вільних у даний момент джерел заявок:

,                                                 (A.12)

де п - загальна кількість джерел заявок;

і - кількість зайнятих джерел;

- параметр потоку джерела у вільному стані.