Информатика и выч. техника \ Информатика

Элементы М-языка MATLAB. Программы MATLAB, страница 5

            help <имя функции>

После комментариев в файле должно располагаться тело функции: совокупность операторов на М-языке, реализующих функцию. В этих операторах можно использовать переменные с зарезервированными именами varargin, varargout, nargin, nargout, которые обозначают, соответственно, списки входных и выходных аргументов, числа входных и выходных аргументов, заданных пользователем при обращении к функции. Самое простое, что можно сделать с этими переменными – проверить, совпадают ли числа входных и выходных аргументов с требуемыми числами, и при несовпадении – прекратить выполнение функции.

Выполнение функции завершается либо после выполнения последнего оператора  в файле, либо при выполнении оператора RETURN, который обычно используется для аварийного прекращения выполнения функции. Вставлять этот оператор в конце файла не требуется!

В составе функции можно задать одну или несколько подфункций, которые записываются в конце файла, после текста основной функции и оформляются по тем же правилам, что и основная функция. Отличие подфункции от основной функции состоит в том, что она не может быть вызвана на выполнение откуда-либо, кроме основной функции.

В качестве примера рассмотрим функцию, реализующую расчет по матрице наблюдений X вектора медиан. Функция записывается в файл с именем median_v.m.

function znach=median_v(X,dim)

% MEDIAN_V - counts the values of median in columns of matrix X.

%X - input matrix,

%dim – dimension of matrix X,

% znach - output values of medians

if nargin==1,

  dim = min(find(size(X)~=1));

  if isempty(dim), dim = 1; end

end

if isempty(X), znach = []; return, end

XX=sort(X);

[m,n]=size(XX);

m1=round(m/2)

if (m1+m1)==m

    znach=(XX(m1,:)+XX(m1+1,:))/2;

else

    znach=XX(m1,:);

end

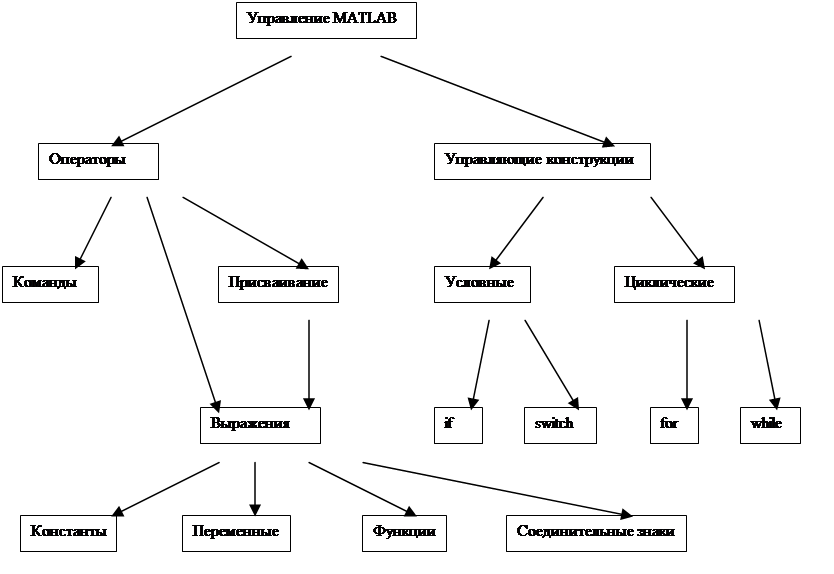
Итак, при разработке программы следует спроектировать ее структуру, то есть определить, какая часть программы будет реализована в главной программе (main), а какие части будут вынесены в отдельные файлы. Далее, для частей, выносимых в файлы, следует определить форму представления каждой из этих частей: сценарий или функция. Запуск на выполнение (передача управления) этих частей может производиться как из головной программы, так и из других частей программы. Поэтому вся программа, решающая интересующую пользователя задачу, может быть представлена в виде многоуровневой иерархической структурной схемы, в которой прямоугольниками (листьями) служат выделенные части программы, а соединительными линиями – пути возможной передачи управления между ними.

2.4. ОБЛАСТИ ДЕЙСТВИЯ ПЕРЕМЕННЫХ

      Переменная, введенная в некоторой части программы действует во всей этой части при условии, что при выполнении этой программы не будет пройден оператор clear с указанием этой переменной или всех переменных. Переменная, действующая в некоторой части программы (в главной программе, сценарии, функции), действует также в других частях, управление которым передается из данной части программы.

В теле функции можно вводить переменные, которые являются, если не оговорено другое, локальными в этой функции. Использовать эти переменные можно только в функции, а при ее завершении занимаемая ими часть рабочей области освобождается. Если их значения требуются вне функции, то эти переменные должны быть объявлены глобальными с помощью оператора

global <список переменных>.

Аналогичное объявление следует сделать также в другой части программы, в которой они должны использоваться.

2.5. Пример программирования при решении задачи

Пусть необходимо решить следующую задачу.

Разработать М-программу, реализующую следующие операции:

·  Ввод из файла tverd.txt элементов ряда наблюдений Y1, Y2,..., YN,  контролируемого показателя Y.

·  Расчет по введенным элементам среднего арифметического значения M :

M=(Y1+ Y2+…+ YN)/N, 

·  Расчет по введенным элементам характеристики рассеяния около среднего - дисперсии S2 :

S2 =[( Y1-M)2+( Y2-M)2+….+( YN-M)2]/(N-1)

·  Расчет оценок 5 ординат характеристики взаимосвязи элементов ряда наблюдений - автокорреляционной функции по формулам:

R(1)=1,

R(2)={(Y1-M)*( Y2-M)+ (Y2-M)*( Y3-M)+...+ (YN-1-M)*( YN-M)}/[(N-1)*S2],

R(3)={(Y1-M)*( Y3-M)+ (Y2-M)*( Y4-M)+...+ (YN-2-M)*( YN-M)}/[(N-2)*S2],

R(4)={(Y1-M)*( Y4-M)+ (Y2-M)*( Y5-M)+...+ (YN-3-M)*( YN-M)}/[(N-3)*S2],

R(5)={(Y1-M)*( Y5-M)+ (Y2-M)*( Y6-M)+...+ (YN-4-M)*( YN-M)}/[(N-4)*S2]

·  Построить график рассчитанной функции R(i).

Решение

x=load('tverd.txt');

nn=size(x);

sred=mean(x);

disp=std(x);

disp=disp*disp;

fprintf('Mean=%10.3f ,   variance=%12.1f\n',sred,sko);

for i=1:5

    R(i)=0;   

    for  j=i:nn(1)

        R(i)=R(i)+(x(j)-sred)*(x(j-i+1)-sred);

    end

    R(i)=R(i)./((nn(1)-i)*disp);

    fprintf('Value of Ordinate %d  = %10.3f\n',i,R(i))

end

plot(R)

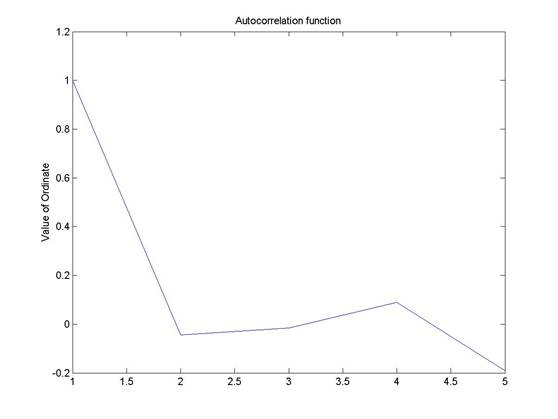
title('Autocorrelation function')

ylabel('Value of Ordinate')

Результаты решения:

Mean=     0.000 ,   variance=         1.0

Value of Ordinate 1  =      1.000

Value of Ordinate 2  =     -0.044

Value of Ordinate 3  =     -0.016

Value of Ordinate 4  =      0.089

Value of Ordinate 5  =     -0.191


 

Скачать файл