Аналоговые эксперименты. Подобие плазменных процессов, страница 2

и соответствующий критерий аналогии, известный как число Льюиса (Le)

.

При изучении процесса диффузии или теплопроводности с помощью электрических аналогов необходимо от детерминированной среды перейти к дискретной через набор элементов электрической схемы, подобранных специальным образом для конкретно решаемой задачи.

13.2. Аналогии между потенциальными полями и полями линий тока

Для стационарных процессов уравнения переноса трансформируются в очевидные дифференциальные выражения

, , .

То есть поле температуры, электрическое поле и поле концентрации диффундирующего вещества подчиняются одному и тому же дифференциальному уравнению, известному как уравнение Лапласа, описывающее так же потенциал и электрическое поле при отсутствии объемных зарядов ().

13.3. Траектории заряженных частиц в магнитных полях

         Траектории заряженных частиц, помещенных в постоянное магнитное поле, можно представить с помощью аналогии с равновесной формой натянутой проволочки, по которой течет ток, помещенной в это поле. Запишем уравнение движения частицы, обладающей импульсом  

,

где  – заряд;  – скорость носителей заряда;  – магнитная индукция.

         Представим траекторию частицы как функцию длины дуги , тогда с учетом равенств

; ; ;

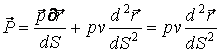
получим уравнение траектории частицы

.

На элемент длины  проводника, по которому течет ток , действует сила, равная

.

При наличии равновесия эта сила должна быть равна силе  натяжения нити. Причем равновесие соблюдается для любого элемента проволоки. Результирующая сила зависит от кривизны элемента и задается соотношением

.

Условие равновесия  позволит нам получить уравнение дуги изгиба проволоки

.

         Таким образом, траектория заряженной частицы и форма проволоки описываются одной и той же кривой, если выбраны одинаковые начальные условия

.

ЛЕКЦИЯ 14

Подобие плазменных процессов

14.1. Подобие в газовом разряде

         Плазменные явления относятся к достаточно сложным физическим явлениям для их опытного изучения. Поэтому роль подобия процессов в них при познании характерных особенностей явления достаточно велика. Уже на ранних стадиях изучения образования и поведения плазмы Таунлид сравнил геометрически подобные газовые разряды, что позволило установить его общие закономерности. Геометрическое подобие разряда в газах предполагает, что средние длины свободного пробега носителей зарядов и нейтральных частиц описываются одним и тем же коэффициентом подобия . Известно, что величина  обратно пропорциональна концентрации  (плотности газа ), то должно выполняться соотношение