+ = – 9,52·10– 4 (рад);
Δφ3 = θ3·l = 17,3·10–3· 0,5 = 8,65·10–3 (рад);
Δφ4 = θ4·l = – 3,66·10–3 · 0,5 = – 1,83·10–3 (рад).
φ1 = Δφ1 = – 5,85·10–3 (рад);
φ2 = Δφ1 + Δφ2 = – 5,85·10–3 – 9,52·10– 4 = – 6,80·10–3 (рад);
φ3 = φ2 + Δφ3 = – 6,80·10–3 + 8,65·10–3 = 1,85·10–3 (рад);
φ4 = φ3 + Δφ4 = = 1,85·10–3 – 1,83·10–3 ≈ 0 (рад).
На эпюре углов закручивании на втором участке экстремум – точка минимума. Найдем значение минимума:
Tk2 = –MA + m(z2 – l);
Tk2 = 0;
–MA + m(z2* – l) = 0;
z2* = +l;
z2* = + 0,5= 0,765 (м);
Δφ2*=![]() dz = – + – – +
dz = – + – – +
+ = – + – –
– = – 4,58·10–3 (рад).
φ2* = φ1 + Δφ2* = – 5,85·10–3 – 4,58·10–3 = – 10,1·10–3.
Строим эпюры рассчитанных параметров, рис. 1.4
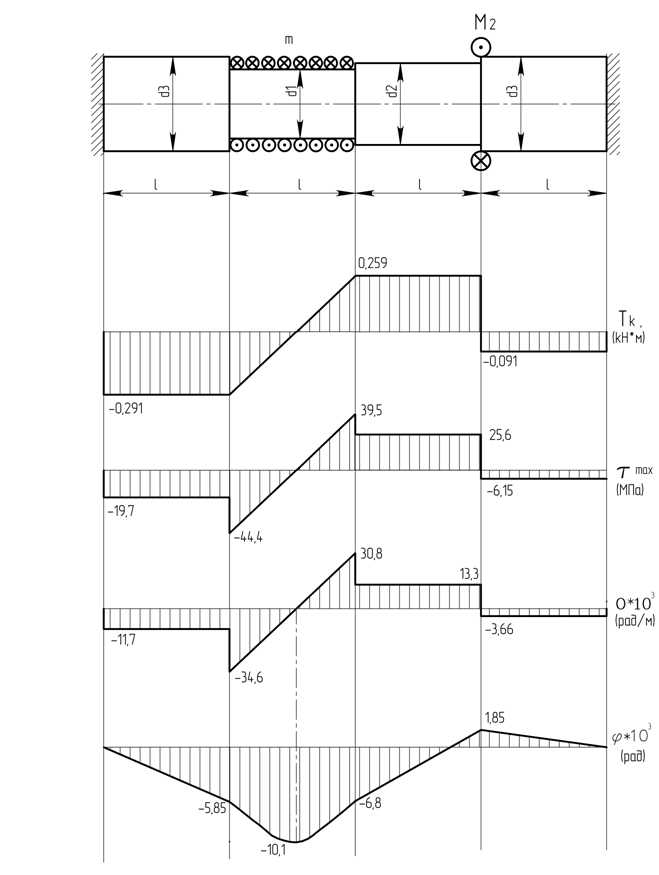
Рисунок 1.4.
Растяжение – сжатие.
Отбросив левую опору и заменив ее реакцией RA, запишем уравнение совместности деформаций. Изображаем реакцию RA (см. рис 1.5).
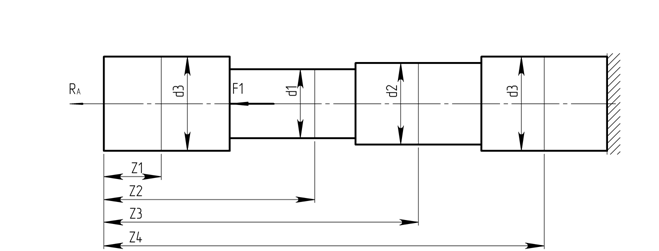
Рисунок 1.5
Уравнение совместимости деформаций:
ΔlA = 0;
ΔlA = + + + = 0.
Находим значения продольных сил:
N1 = RA;
N2 = RA+ F1;
N3 = RA+ F1;
N4 = RA+ F1.
Перепишем выражение совместности деформаций с учетом найденных продольных сил:
ΔlА = + + + = 0
Умножим на Е и разделим наl получившееся выражение:
+ + + = 0
Подставляем найденные значения и найдем RA :
+ + + = 0;
3,63·RA = –2,61·105;
RA = –72 (кН).
Отбрасываем правую опору и заменяем ее реакцией RB (см. рис. 1.6)
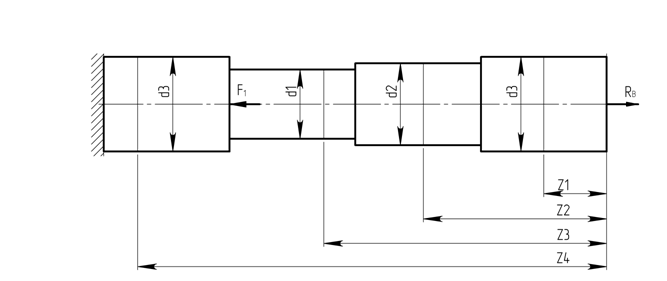
Рисунок 1.6.
Запишем уравнение совместности деформаций:
ΔlВ = 0;
ΔlВ = + + + = 0;
Найдем значения продольных сил:
N1 = RB;
N2 = RB;
N3 = RB ;
N4 =RB – F1.
Перепишем выражение совместности деформаций с учетом найденных продольных сил:
+ + + = 0;
Разделим на l и умножим на E получившееся выражение:
+ + + = 0
Подставляем данные значения и находим RB:
+ + + = 0
3,63·RB = 65,2·103;
RB = 18 (кН).
Проверим решение.
∑z = 0; RA – RB + F1 = 0
–72 –18 +90 ≡ 0
Решение верно.
Находим значение продольных сил:
N1 = RA ; N1 = –72 (кН);
N2 = RA+ F1; N2 = –72+90 =18 (кН);
N3 = RA+ F1; N3 = –72+90 =18 (кН) ;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.