Задание.
Задан
брус, нагруженный внешними моментами и осевыми силами, как указано на рис. 1.1 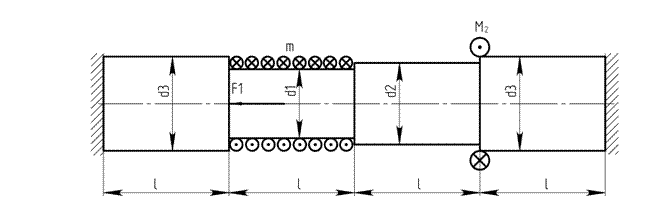
Рисунок 1.1
Требуется:
1. раскрыть статическую неопределимость бруса;
2. определить внутренние силовые факторы, напряжения и перемещения;
3. исследовать напряженное состояние в опасных точках и оценить прочность по гипотезе наибольших касательных напряжений, приняв [σ] = 120 МПа.
Дано:
m = 1,1 ;
M2 = 0,35 kH·м;
F1 = 90 kH;
d1 = 0,032 м;
d2 = 0,037 м;
d3 = 0,042 м;
l = 0,5 м;
E = 2·105 MПа;
G = 8·104MПа.
Решение.
Находим геометрические характеристики поперечных сечений.
Моменты инерции:
Jp = 0,1·(d)4:
Jp1 = Jp4 = 0,1·(0,042)4 = 3,11·10-7 (м4);
Jp2 = 0,1·(0,032)4 = 1,05·10-7 (м4) ;
Jp3 = 0,1·(0,037)4 = 1,87·10-7 (м4).
Моменты сопротивления:
Wp = 0,2·(d)3;
Wp1 = Wp4 = 0,2*(0,042)3 = 1,48·10-5 (м3) ;
Wp2 = 0,2·(0,032)3 = 6,55·10-6 (м3) ;
Wp3 = 0,2·(0,037)3 = 1,01·10-5 (м3) ;
Площади поперечных сечений:
A = ;
A1 = A4 = = 1,38·10-3 (м2) ;
A2 = = 8,04·10-4 (м2) ;
A3 = = 1,07·10-3 (м2) ;
Задача статически неопределима один раз.
Раскрытие статической неопределимости.
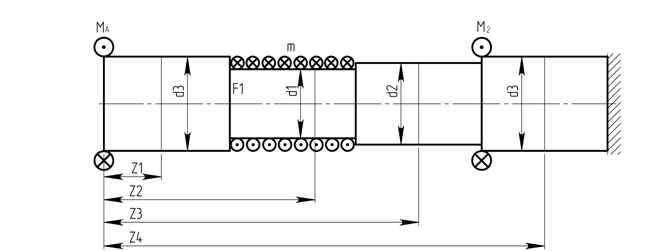
Кручение. Отбросим левую опору и заменим ее реактивным моментом MA (см. рис. 1.2)
 Р
Р
Рисунок 1.2.
Составим уравнение совместности деформаций, приравняв к нулю перемещение левого конца вала:
φА = Δφ1 + Δφ2 + Δφ3 + Δφ4 = 0;
φA = + + + = 0.
Составим выражения для крутящих моментов:
Tk1 = – MA;
Tk2 = – MA + m·(z2 –l) ;
Tk3 = – MA + m·l;
Tk4 = – MA + m·l – M 2 .
Тогда уравнение совместимости деформаций для левого конца вала примет вид:
φА =
+ ![]() + + = 0
+ + = 0
– – + – + – + – =0
Разделим получившееся выражение на l и умножим на G:
– – + – + – + – =0;
Подставим найденные значения в получившееся выражение и найдем МА:
– – + – + – + – =0;
– 2,13·107·МА = –6,20·109;
МА = 291 (H·м).
Отбросим правую опору и заменим ее реактивным моментом MB (см рис. 1.3)
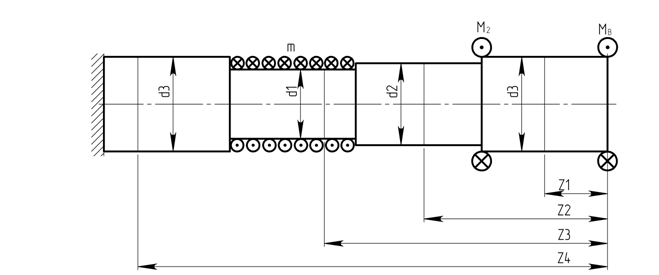 Рисунок 1.3.
Рисунок 1.3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.