Осуществление прогноза с помощью моделей и сравнение рассчитанных значений с экспериментальными. Исследование свойств математической модели

6)Осуществление прогноза с помощью моделей и сравнение рассчитанных значений  с экспериментальными:

Данный пункт является неотъемлемой частью исследования системы, так как после построения модели всегда следует провести проверку соответствия  полученной модели и реального объекта. Проверка модели представляет собой процесс, который позволяет нам быть уверенными в том, что любой вывод о поведении системы, сделанный на основе моделирования, будет правильным.

            Перед нами не стоит задачи доказать, что данная имитация является правильным отображением реальной системы. Вместо этого нас интересует справедливость выводов и решений, полученных на модели объекта.

            В нашем случае мы должны провести на модели проверку с тем, чтобы выяснить ее соответствие реальному объекту.:

o  Мы должны убедиться, что модель вырабатывает выходные сигналы, схожие с реальной моделью при одинаковых входных параметрах. Это соответствие желательно требовать и при предельных значениях параметров системы.

o  Мы должны убедиться, что в модели выбранные параметры сигналов (математическое ожидание, дисперсия, корреляционная функция) совпадают с параметрами исходной модели. Для проверки таких гипотез следует использовать статистические методы.

Проверка критерия о нормальности законов распределения y1, y2 будет произведена в следующем пункте, здесь мы сравним истинные значения выходных переменных, полученных в результате опытов, с моделями.

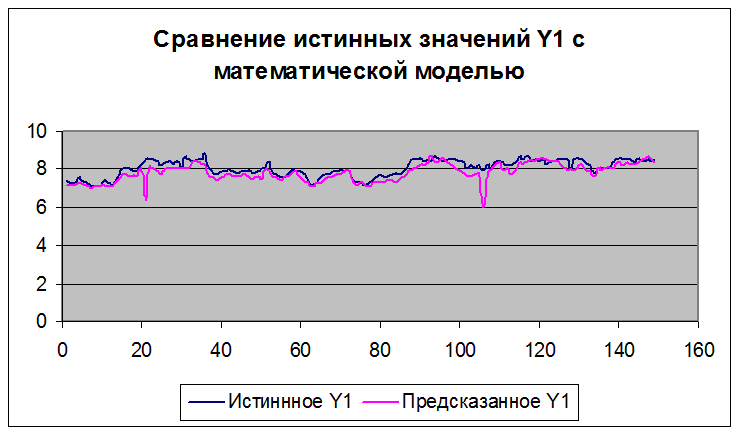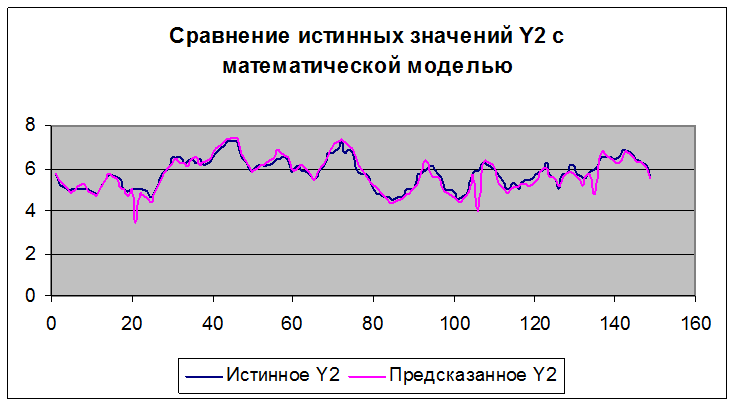
7)Исследование свойств математической модели.

(Проверка критерия о нормальности законов распределения y1, y2)

Был поставлен опыт для проверки критерия согласия. Число точек N = 150 с интервалом дискретизации 1 секунда. Приложение 19.

Число квантов К = 1+3,2*lgN = 5.96

Берем К = 6.

Ширина интервалов: LY=(Ymax-Ymin)/K

 LY1= 0.28

 LY1= 0.47

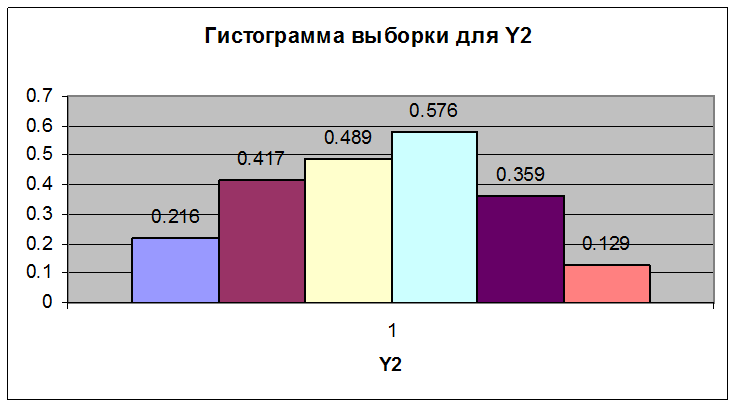
Были построены гистограммы выборки по Y1 и Y2.

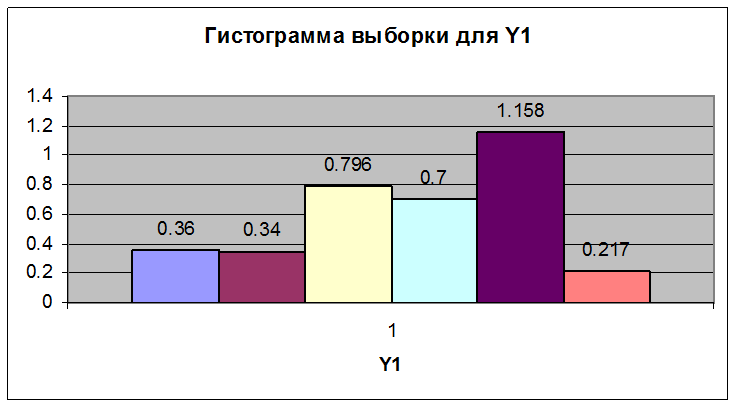
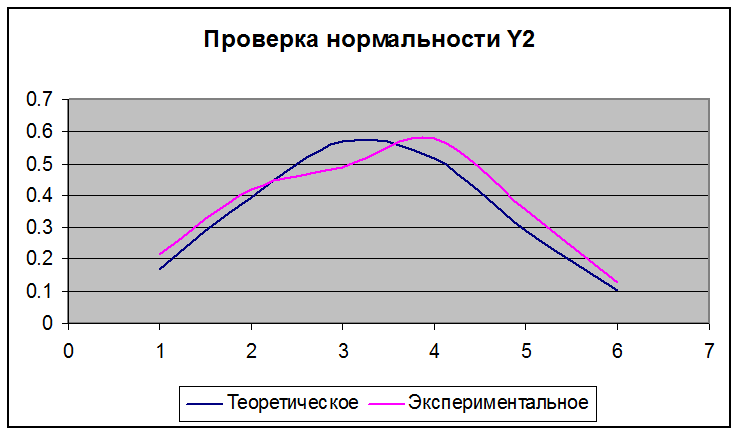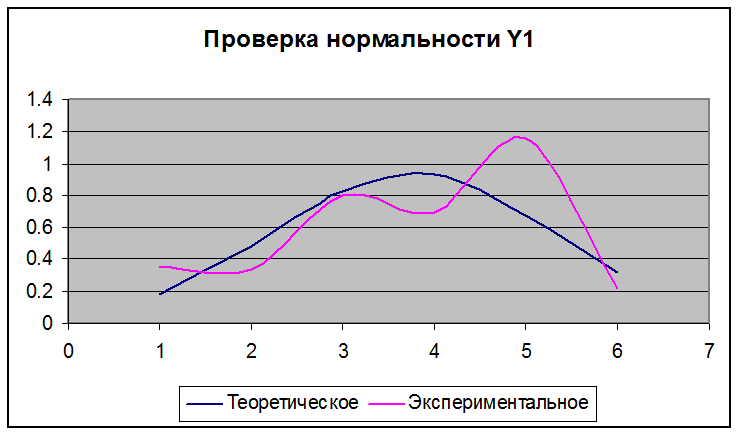
Проверку гипотезы о нормальности закона распределения y1 и y2 осуществляем с помощью критерия Пирсона.

Гистограмма Y1
n	Y1	f(Y1)	Pm	G
15	7.12	0.36	0.06742	2.527347
14	7.4	0.34	0.134465	1.749663
33	7.68	0.796	0.22884	0.022261
29	7.96	0.7	0.255738	2.068951
48	8.24	1.158	0.187686	14.72218
9	8.52	0.217	0.125851	4.974696
	8.8		1	26.0651

Гистограмма Y2
n	Y2	f(Y2)	Pm	G
15	4.48	0.216	0.110384	0.109388
29	4.95	0.417	0.184436	0.10631
34	5.42	0.489	0.26313	0.627463
40	5.89	0.576	0.239036	0.604013
25	6.36	0.359	0.138259	1.006285
9	6.83	0.129	0.064755	0.03556
	7.3		1	2.489019

Расчет gкр.

Gкр для 5 степеней свободы и уровня значимости 0,05 составляет 11,07.

Вывод: согласно критерию Пирсона,

 так как g(y1) = 26,0651 > gкр = 11,07, то гипотеза о нормальности распределения величины y1 противоречит наблюдениям и должна быть отвергнута.

 так как g(y2) = 2,489019 < gкр = 11,07, то гипотеза о нормальности распределения величины y2 принимается как не противоречащая наблюдениям.

Временная картина для Приложения 19:  

·  Исследование динамических свойств выходного параметра y3 (канал y3-u2).

     Для идентификации динамических характеристик объектов управления используются специальные входные сигналы: ступенчатые, импульсные, синусоидальные. Ступенчатый сигнал является наиболее простым для применения, поэтому мы и использовали его в нашей работе. Здесь мы сняли кривую разгона и по ней графо-аналитическим методом определили параметры динамического звена (передаточную функцию звена). Однако этот метод используется в основном только в лабораторных исследованиях, так как на реальном объекте его применение ведет к увеличению себестоимости производства, а зачастую и к выходу за предельные границы допустимых ограничений, то есть к остановам производства и авариям.

Для снятия был взят период опроса (время дискретизации), равный 1 секунде, выбор  сделан из условия непрерывности процесса. 

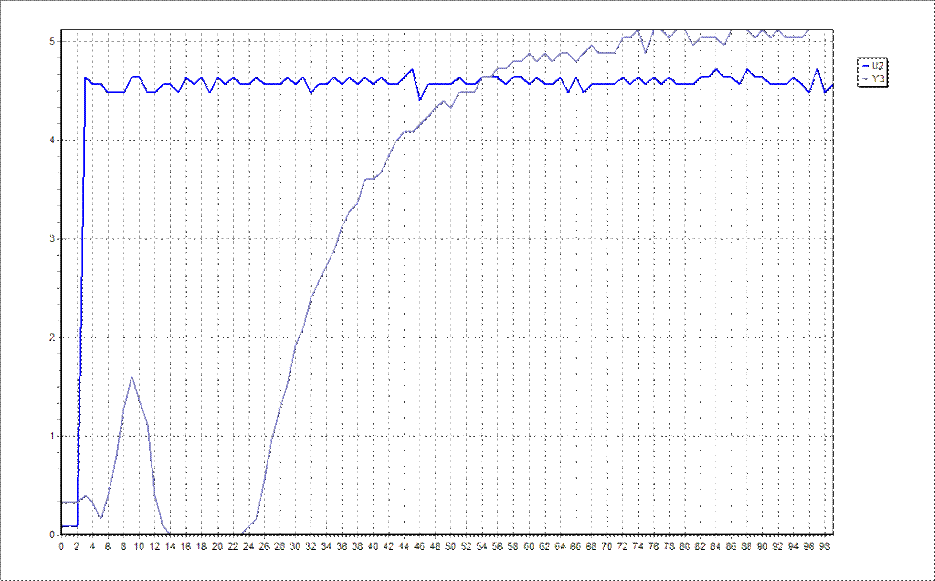
 Полученная разгонная характеристика: (Приложение 21)

Аналитический вид передаточной функции: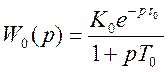

Установившиеся значения:

U2 = 4.64

Y3 = 5.12 , следовательно 

коэффициент передачи K₀ = 1.1

Графоаналитическим методом определяем:

время запаздывания             t₀ = 21 c

постоянная времени T₀= 12 c

Полученная передаточная функция  ТОУ: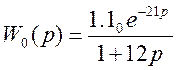   

Временная картина для Приложения 21

:

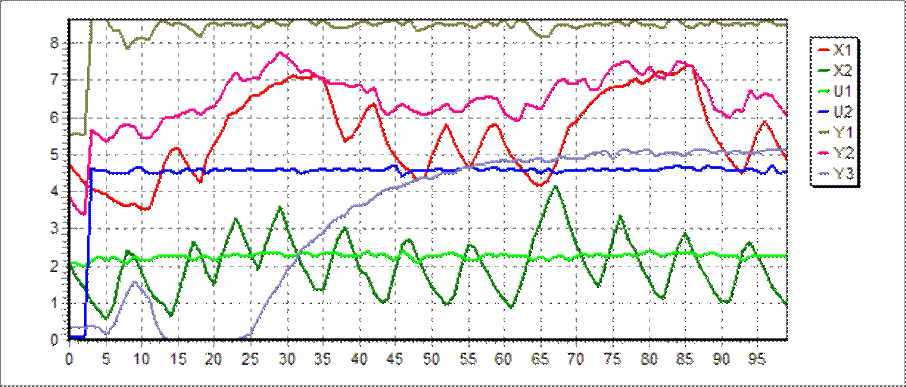·  Оптимизация выбранного критерия оптимальности ТОУ

Постановка задачи оптимизации:

План задачи: X1, X2, U1, U2

Критерий оптимизации: Y1(X1, X2, U1, U2) ® max

Y1 = 0.33745*X1 – 0.12717*X2 + 0.56295*U1 + 0.54609*U2 + 3.2222

Ограничения на управляемые переменные:

1 £X1 £ 3

1 £X2 £ 4.5

1.5 £U1 £ 4

2 £U2 £ 4

Функциональные ограничения находим методом линейного программирования:

a) Y2 = 0.37769*X1 + 0.39776*X2 + 0.44069*U1 + 0.41796*U2 + 0.41764 ® max

  при

X1  £ 3

X2  £ 4.5

U1  £ 4

U2  £ 4

Решение: X1 = 3, X2 = 4.5, U1 = 4, U2 = 4

Y2_max = 6.775

б) Y2 = 0.37769*X1 + 0.39776*X2 + 0.44069*U1 + 0.41796*U2 + 0.41764 ® min

  при

1 £X1 

1 £X2 

1.5 £U1 

2  £U2 

Решение: X1 = 1, X2 = 1, U1 = 1.5, U2 = 2

Y2_min = 2.69

 Постановка стохастической задачи оптимизации

Т.к. превышения пороговых значений Y2 приводит к существенным потерям, то по технологическим соображениям задачу стохастической оптимизации формулируем в виде задачи оптимизации по вероятности (Р - модель):

Y1(X1, X2, U1, U2) ®max

Ограничения на управляемые переменные:

1 £X1 £ 3

1 £X2 £ 4.5

1.5 £U1 £ 4

2 £U2 £ 4

Функциональные ограничения:

P { Y2(X1, X2, U1, U2) £ Y2_max } ³ p           

P { Y2(X1, X2, U1, U2) ³ Y2_min } ³ p

p = 0.9 – доверительная вероятность

 Оптимизация по регрессионным моделям

1.         Искусственное сведение стохастической задачи к детерминированной

Y1 = 0.33745*X1 – 0.12717*X2 + 0.56295*U1 + 0.54609*U2 + 3.2222 ®max

Ограничения на управляемые переменные:

1 £X1 £ 3

1 £X2 £ 4.5

1.5 £U1 £ 4

2 £U2 £ 4

Функциональные ограничения:

Y2(X1, X2, U1, U2) £  Y2_max – g(p)*s₂

Y2(X1, X2, U1, U2)³  Y2_min + g(p)*s₂

p = 0.9 – доверительная вероятность

g(p) – квантиль нормированного нормального распределения

Решение: X1 = 2.871, X2 = 1, U1 = 4, U2 = 4

Y1(X1, X2, U1, U2) = 8.5

2.         Исследование чувствительности оптимального решения к ошибкам

Пусть коэффициенты регрессионной модели меняются в некоторых ограниченных пределах   :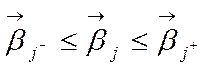

  

     

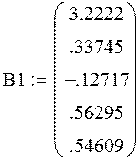
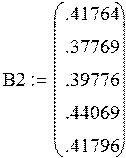
тогда для определения пределов изменения критерия оптимизации необходимо решить две задачи: с «широкой» допустимой областью (коэфф-ты ограничений равны ) и критерием с коэффициентами 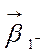, и с «узкой» допустимой областью () и критерием с коэффициентами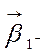

а) Y1 = 0.233*X1 – 0.214*X2 + 0.441*U1 + 0.432*U2 + 2.255 ®max

Ограничения на управляемые переменные:

1 £X1 £ 3

1 £X2 £ 4.5

1.5 £U1 £ 4

2 £U2 £ 4

Функциональные ограничения:

Y2(X1, X2, U1, U2) £  Y2_max – g(p)*s₂

Y2(X1, X2, U1, U2)³  Y2_min + g(p)*s₂

Y2 = 0.488*X1 + 0.49*X2 + 0.57*U1 + 0.539*U2 + 1.122

p = 0.9 – доверительная вероятность

g(p) – квантиль нормированного нормального распределения

Решение: X1 = 1, X2 = 1, U1 = 1.89, U2 = 4

Y1(X1, X2, U1, U2) = 5.138

б) Y1 = 0.442*X1 – 0.04*X2 + 0.685*U1 + 0.661*U2 + 3.886 ® max

Ограничения на управляемые переменные:

1 £X1 £ 3

1 £X2 £ 4.5

1.5 £U1 £ 4

2 £U2 £ 4

Функциональные ограничения:

Y2(X1, X2, U1, U2) £  Y2_max – g(p)*s₂

Y2(X1, X2, U1, U2)³  Y2_min + g(p)*s₂

Y2 = 0.267*X1 + 0.306*X2 + 0.312*U1 + 0.296*U2 - 0.287

p = 0.9 – доверительная вероятность

g(p) – квантиль нормированного нормального распределения

Решение: X1 = 3, X2 = 3.869, U1 = 4, U2 = 4

Y1(X1, X2, U1, U2) = 10.435

3.         Испытание статистических гипотез в задаче стохастической оптимизации

План задачи: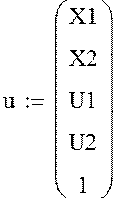  

Критерий оптимизации:

max

 

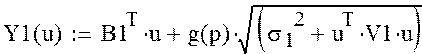
Ограничения на управляемые переменные:

1 £X1 £ 3

1 £X2 £ 4.5

1.5 £U1 £ 4

2 £U2 £ 4

Функциональные ограничения:

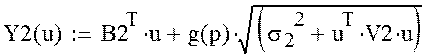  £Y2_max

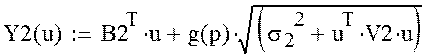  ³Y2_min

 -- дисперсия Y1 и Y2 соответственно

  V1, V2 – ковариационная матрица коэффициентов

Решение: X1 =2.783, X2 = 1, U1 = 4, U2 = 4

Y1(X1, X2, U1, U2) = 9.55

·  Исследование и выбор оптимального закона регулирования регулятора

Период опроса выбирается аналогично предыдущему пункту( интервал дискретизации равен 1 секунде из условия непрерывности процесса), интервал квантования по уровню задается равным 1%.

1.  Выбор внешних показателей качества процесса.

Были выбраны :

§  Для П-регулятора переходный процесс (ПП) с 20% перерегулированием и с минимальным временем ПП

§   Для ПИ-регулятора ПП с 20% перерегулированием и без перерегулирования

§  Для ПИД-регулятора с 20% перерегулированием и без перерегулирования

2.  Нахождение оптимальных параметров настроек регуляторов  различными законами для регулирования переходного процесса с выбранными свойствами.

§  П-регулятор:
с 20% перерегулированием – К_р = 0.41
с минимальным временем   – К_р = 0.78

§  ПИ-регулятор:
с 20% перерегулированием – К_р = 0.45,    Т_и = 10.27
без перерегулирования        –  К_р = 0.246, Т_и = 10.73

§  ПИД-регулятор
с 20% перерегулированием – К_р = 0.5,    Т_и = 16.8 , Т_д = 5.44
без перерегулирования        – К_р = 0.36,  Т_и = 16.6,  Т_д = 4.2

с минимальным временем   – К_р = 1,51  Т_и = 19,2,  Т_д = 7,9

3.  Полученные по итогам эксперимента результаты.