Исследование функции и построение её графика, страница 2

Таблица №1

  Вычислим .

8.Вторая производная:

   Критические точки 2-го рода: х=0

    Исследование перемены знака y” при переходе через критические точки 2-го рода представлено в таблице №2.

Функция	Интервал
		0
y”	-		+
y		Перегиба нет

Таблица №2

  Таким образом,  график функции вогнутый при и  выпуклый при . Точек перегиба нет.

9. График функции:

Задание №2.

1.Функция определена для всех

2.График функции пересекает ось Оу в точке (0;0) и ось Ох в точке (2;0)

3.Функция общего вида, т.к.

4.Функция непериодическая.

5.Функция непрерывная, т.к. определена для всех .Следовательно, график функции вертикальных асимптот не имеет.

6.   Следовательно, наклонных асимптот нет.

7.Производная: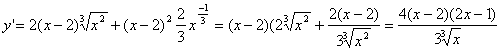 

   Критические точки функции : х=2, х=0, . Исследование перемены знака  при переходе через критические точки представлено в таблице №1.

Функция	Интервал
		0				2
y’	-		+	0	-	0	+
y