





|
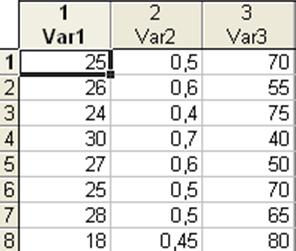
Исходные данные: |
|
|
|
|
|
|
|
|
|
|
|
1.Оценим средние значения и дисперсии для признаков X(1),X(2),X(3). Рассчитаем корреляционную матрицу для анализируемого трехмерного признака. |
|
Расчет среднего: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет дисперсии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет корреляционной матрицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ковариационная матрица: |
|
|
|
|
|
Парные коэффициенты корреляции: |
|
|
|
|
|
|
|
Корреляционная матрица: |
|
|
|
|
|
2. Вычислим матрицу частных коэффициентов, т.е. оценить значения r ik /l. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Частные коэффициенты корреляции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Проанализируем значения парного и частного коэффициентов корреляции: |
|
|
|
- парный коэффициент корреляции |
|
|
|
- частный коэффициент корреляции |
Т.к. частный коэффициент корреляции меньше, чем соответствующий парный коэффициент корреляции, то взаимосвязь между двумя величинами обусловлена частично воздействием на эту пару остальных, фиксируемых, случайных величин.
Проверка гипотезы
|
Ho : p13=0 |
|
ta/2(a = 0.05, N-2= 7) =2.446 |
|
g1 >= ta/2 |
|
|
|
|
|
|
|
|
|
|
|
Ho : |
|
ta/2(a = 0.05, N-L-2= 5) =2.57 |
|
g2 >= ta/2 |
|
|
|
|
|
|
|
4. Найдем точечную оценку множественного коэффициента корреляции и проверим гипотезу (при уровне значимости a = 0,05) о его статистической значимости. |
|
Множественный коэффициент корреляции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка гипотезы: |
|
Ho : Rm=0 |
|
|
|
F(a = 0.05, 8-3-1, 3) = 9.12 |
|
|
|
g >= Fpredp |
|
|
|
|
|
гипотеза отвергается |
|
|
|
|
|
гипотеза не отвергается |
|
|
|
|
|
гипотеза отвергается |
|
5. Расчет коэффициентов парной регрессии и проверка значимости полученного уравнения(при a=0.05). X(3)=b0+b1X(1) |
|
|
|
|
|
|
|
|
|
|
|
I?iaa?ea aeiioacu: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(a = 0.05, 1, 6) =5.99 |
|
|
|
6. Выведем уравнения для вычисления главных компонент f(1), f(2), f(3) по заданным значениям исходных показателей x(1), x(2), x(3). |
|
|
|
Собственные числа: |
|
|
|
|
|
Собственные вектора: |
|
|
|
|
|
|
f1 = - 0.543 * X1 - 0.581* X2 + 0.606 * X3
f2 = 0.813* X1 - 0.543* X2 + 0.208 *X3
f3 = 0.208 * X1 + 0.606 * X2 + 0.768 *X3
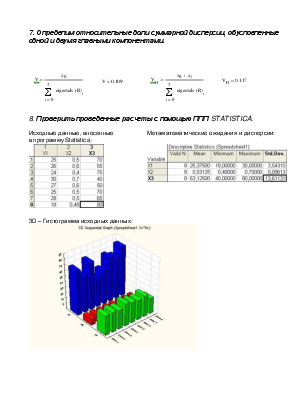
7. Определим относительные доли суммарной дисперсии, обусловленные одной и двумя главными компонентами.
|
|
|
|
|
|
|
|
8. Проверить проведенные расчеты с помощью ППП STATISTICA.
|
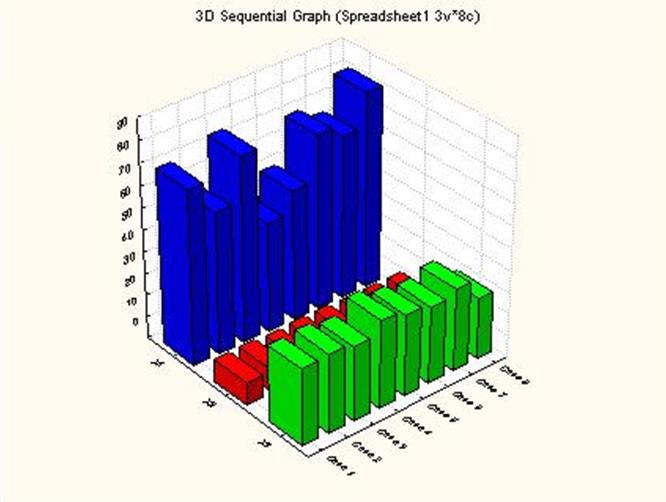
Исходные данные, внесенные в программу Statistica: |
Метаматематические ожидания и дисперсии: |
|
|
|
3D – Гистограмма исходных данных:
|
Вычисление корреляционной матрицы: |
Вычисление Частного коэффициента корреляции для ř13/2: |
|
|
|
Проверка уравнения регрессии:
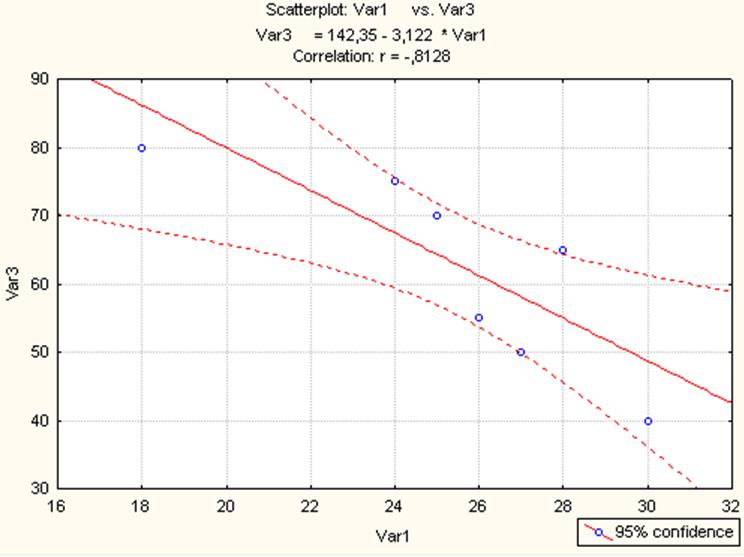
Иерархический кластерный анализ:
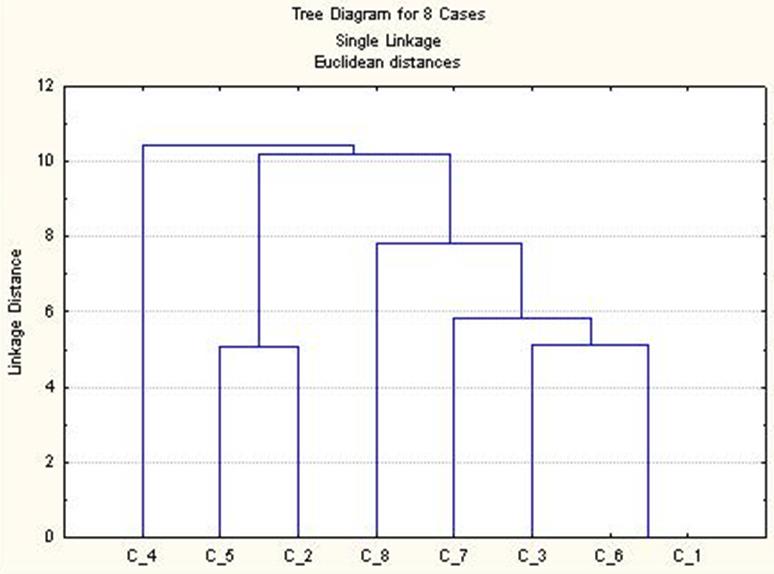
Метод многомерного шкалирования:
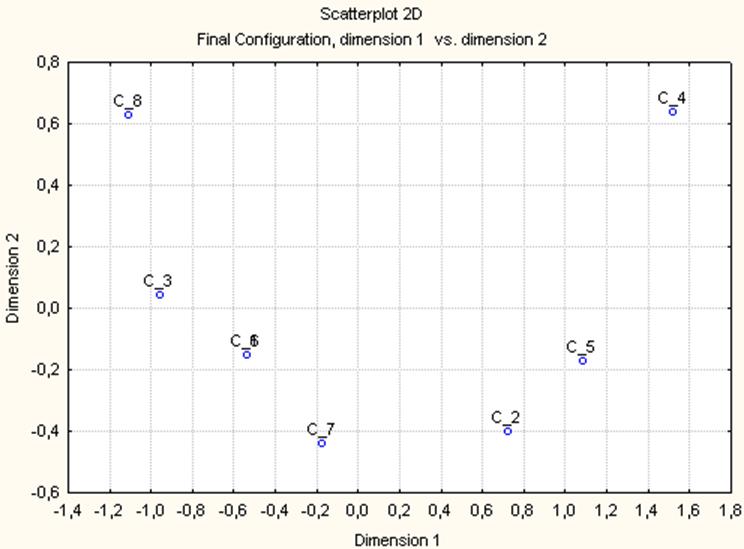
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.