Цифровые устройства. Арифметические основы цифровой техники

Цифровые устройства

Лекция 1

1.1 Арифметические основы цифровой техники

Достоинства цифровых устройств - высокая точность, помехозащищенность при передаче, хранении и обработке информации.

1  .1.1 Системы счисления

Системой счисления называется совокупность правил для представления чисел в виде конечного числа символов.

В цифровой технике используются позиционные системы счисления, где вес разряда зависит от его положения в записи числа, например:

- Десятичная система (DEC), целая часть числа:

 

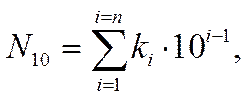где: k – коэффициент, принимает значения символов системы счисления: 0, 1, 2,…, 9;   i – вес разряда, зависящий от позиции (расположения) символа, n - число разрядов числа; 10 – основа системы.

Пример: 902₁₀ = 9·10²+ 0·10¹+ 2·10⁰.

 

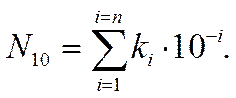Для дробной чисти:

Пример: 0,902₁₀ = 9·10 ^{– 1} + 0·10 ^{– 2} + 2·10 ^{– 3}.

В цифровых устройствах десятичная система применяется в аналого-цифровых и цифроаналоговых преобразователях, в двоично-десятичном коде.

 - Двоичная система (BIN), целая часть числа:

 

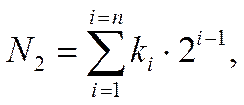где: k - принимает значения символов двоичной системы счисления: 0, 1; i – вес разряда; 2 – основа системы.

Например, 11001110₂. Каждая позиция занята двоичной цифрой, называемой битом. Наименьший значащий бит (младший разряд) расположен справа. Старший разряд – слева.

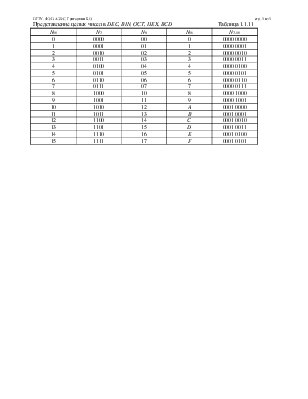
Число DEC равно сумме произведений значений битов числа BIN на их вес (таблица 1.1.1).

Пример преобразования из BIN в DEC                                                                   Таблица 1.1.1

число BIN	1	1	0	0	1	1	1	0
вес	27	26	25	24	23	22	21	20
	128	64	32	16	8	4	2	1
значение	128·1	64·1	32·0	16·0	8·1	4·1	2·1	1·0
результат	Число DEC: 128 + 64 + 8 + 4 + 2 = 206

Пример:902₁₀ = 1·2⁹+ 1·2⁸+ 1·2⁷+ 0·2⁶+ 0·2⁵+ 0·2⁴+ 0·2³+ 1·2²+ 1·2¹ + 0·2⁰.

902₁₀→ 1110000110₂.

Для дробной части двоичного числа веса разрядов: ½, ¼ и т.д. (таблица 1.1.2):

 

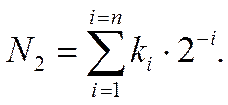Пример преобразования из BIN в DEC                                                                Таблица 1.1.2

число BIN	0	,	0	1	1
вес	20		2-1	2-2	2-3
	1		0,5	0,25	0,125
значение	1·0		0,5·0	0,25·1	0,125·1
результат	Число DEC: 0,25 + 0,125 = 0,375

Пример:0,25 ₁₀ = 0·2⁰, 0·2 ^-1 + 1·2 ^-2  = 0,01₂.

Цифровые устройства оперируют в двоичной системе (хранение, передача, обработка информации). Система применяется для расчетов с малым объемом входных и выходных данных и большим объемом вычислений. Ее достоинства: простота и быстродействие выполнения арифметических операций, наличие надежных микроэлектронных устройств, для представления, передачи и хранения значений двоичного разряда (0, 1). Также имеется математический аппарат анализа и синтеза цифровых устройств (Булева алгебра).

- Шестнадцатеричная (HEX). Основа системы: 16; коэффициенты системы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует символам: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 в десятичной системе.

Преобразование двоичных чисел в шестнадцатеричные числа:

биты двоичного числа объединяются в группы по четыре, при необходимости слева  добавляются нули. Каждую группу заменяют соответствующим шестнадцатеричным символом, или, наоборот, для обратного преобразования (таблица 1.1.3).

Пример преобразования из BIN в NEX                                                                Таблица 1.1.3

число BIN	1111010
объединение в группы	0111	1010
замена символом	7	А
результат	Число NEX: 7А

Пример:199₁₀ = 1·2⁷+ 1·2⁶+ 0·2⁵+ 0·2⁴+ 0·2³+ 1·2²+ 1·2¹ + 1·2⁰ = С7₁₆

199₁₀ → 1100 0111₂ → С7₁₆

Для дробной части числа HEX веса разрядов: 16^-1, 16^-2 и т.д. (таблица 1.1.4):

Пример преобразования из HEX в DEC                                                               Таблица 1.1.4

число HEX	0	,	0	1
вес	160		16-1	16-2
	1		0,0625	0,00390625
значение	1·0		0,0625·0	0,00390625·1
результат	Число DEC: 0 + 0,00390625 = 0,00390625

Пример:0,1₁₆ = 0·16 ⁰, 1·16 ^-1 =  0,0625₁₀.

Данная система используется для представления двоичных чисел в компактном виде при программировании на языках низкого уровня.

- Восьмеричная система (ОСТ). Основа системы: 8; коэффициенты системы: 0, 1, 2, 3, 4, 5, 6, 7.

Преобразование двоичных чисел в восьмеричные числа:

биты двоичного числа объединяются в группы по три, при необходимости слева  добавляются нули. Каждую группу заменяют соответствующим десятичным символом, или, наоборот, для обратного преобразования (таблица 1.1.5).

Пример преобразования из BIN в ОСТ                                                                Таблица 1.1.5

число BIN	11100
объединение в группы	011	100
замена символом	3	4
результат	Число ОСТ: 34

Данная система используется для представления двоичных чисел в компактном виде при программировании на языках низкого уровня. Применяется редко, т.к. число разрядов  цифровых устройств обычно кратно четырем (для преобразования удобнее HEX).

- Двоично-десятичная (BCD).

Преобразование десятичных чисел в двоично-десятичные числа:

каждый разряд десятичного числа заменяется соответствующим четырехразрядным двоичным числом, или, наоборот, для обратного преобразования (таблица 1.1.6).

Пример преобразования из DEC в BCD                                                               Таблица 1.1.6