Изучение дисперсии света (лабораторная работа), страница 8

          Далее для упрощения вычислений положим , при этом изменение фазы колебания вблизи резонансной частоты  будет даваться изменением знака амплитуды А. Получим:

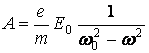.                                              (10)

Электрон под действием падающей волны будет совершать колебательное движение:

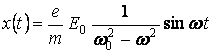.                                 (11)

В результате смещения электрона происходит разделение зарядов в молекуле и возникает единичный дипольный момент:

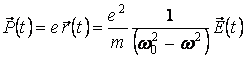,                           (12)

где  – электрическое поле электромагнитной волны. Далее считаем, что .

          Вектор поляризации вещества, это дипольный момент единицы объема вещества, который можно вычислить умножив единичный дипольный момент на количество смещающихся электронов в единице объема:

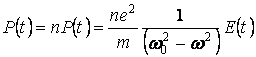.                         (13)

Отсюда диэлектрическая проницаемость вещества равна:

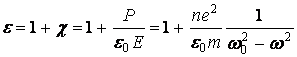;                          (14)

          Учитывая связь между  и показателем преломления п, , получим:

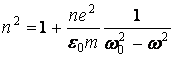.                                         (15)

Или через длину волны  это выражение для п² можно записать в виде:

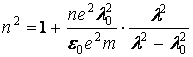.                                     (16)

В формулу (15), во второе слагаемое входит множитель размерности , который дает важную характеристику вещества:

,                                               (17)

которая называется плазменной или ленгмюровской частотой. Эта частота связана с собственными коллективными колебаниями электронов в веществе.

          Так, удивительным образом, оказывается, что величина, характеризующая коллективные движения электронов в плазме попадает в уравнение (16), выражающее зависимость показателя преломления от длины волны, хотя мы рассматривали колебательные движения с атомами вещества электронов. Этот результат можно объяснить тем, что колебания плазмы аналогичны поляризации диэлектрика.

          Теперь вернемся у формуле (16). Можно показать, что зависимость  в области нормальной дисперсии (длина волны излучения  достаточно далеко от характеристической длины волны, введенной по определению 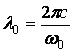) может быть приближенно выражена формулой:

.

Наша работа ставит своей целью подтвердить этот вывод теории и следует сказать, что аккуратно поставленный эксперимент дает возможность это сделать.