Изучение дисперсии света (лабораторная работа), страница 7

ПРИЛОЖЕНИЕ К ЛАБОРАТОРНОЙ РАБОТЕ № 39

ЭЛЕМЕНТАРНАЯ КЛАССИЧЕСКАЯ ТЕОРИЯ ДИСПЕРСИИ

(доц. Мельников Ю.П., доц. Шувалов В.В.)

          Как показал Г. Лоренц, использование классических представлений о строении вещества достаточно для качественного понимания многих оптических явлений. В частности, это относится и к дисперсии света, т.е. к зависимости показателя преломления вещества от длины волны излучения.

          При прохождении через вещество световой волны не каждый электрон, входящий в частицы вещества (молекулы или атома) действует дополнительная сила электрической природы

.                                           (1)

На основании второго закона Ньютона можно получить уравнение вынужденных колебаний электрона:

,                                (2)

где т – масса электрона; – коэффициент затухания колебаний;  – частота собственных колебаний электрона в молекуле (атоме).

          Решение уравнения (2) состоит из суммы общего решения однородного уравнения (), которое запишется

,                                        (3)

где

и частного решения неоднородного уравнения (2):

.                                     (4)

Общее решение однородного уравнения дает решения, затухающие за время , которое очень мало. Таким образом, стационарное решение уравнения (2) должно включить только незатухающие частные решения (4). Подставляя частное решение (4) в уравнение (2) получим тождество:

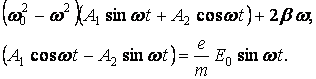                       (5)

          Так как это тождество должно удовлетворяться в любой момент времени, то должны быть равны отдельно коэффициенты при  и  в левой и правой частях тождества (5). Отсюда получим систему уравнений для А₁ и А₂:

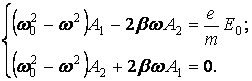                          (6)

Решаем эту систему, например, подставляя решения для А₂ из второго уравнения в первое, получим выражения для  А₁ и А₂:

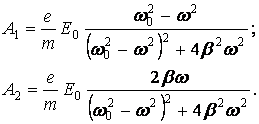                         (7)

Представим частное решение неоднородного уравнения (4) с помощью комплексных амплитуд, т.е. считаем, что  и . Тогда частное решение уравнения (2) можно записать в виде

,                                                 (8)

где  – суммарная амплитуда, а 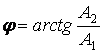 – дополнительная фаза, возникающая при наличии затухания.

Для А и , используя формулы (7), получим:

.

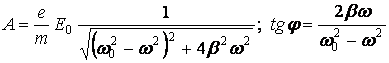Из решения (8) с учетом формулы для А и  (9) и уравнения колебаний (2) видно, что при больших временах  амплитуда вынужденных колебаний сильно зависит от разности , а фаза колебаний зависит от знака разности () и может быть такова, что электрон будет колебаться в противофазе с вынуждающей силой электромагнитной волны, что будет при . Так как смещение электронов приводит к поляризации диэлектрика, то от фазы колебания электронов зависит и поляризация диэлектрика.