Министерство науки и высшего образования РФ
НГТУ
Отчет по курсовой работе
Факультет ФТФ
Группа ФЛ-61
Студент Подчасов А.
Преподаватель Корель И.И.
Дата 02.06.08
Новосибирск
2008
Рабочее задание
Нарисовать семилепестковую розу: ρ = a*sin(4φ) , a = 1.6. Найти полную длину кривой. Вычислить координаты точек пересечения нечётных лепестков.
Ход работы
1. Используя интегральное исчисление мы вычислили длину кривой. И далее рассчитали совпадающие точки на нечетных лепестках розы.
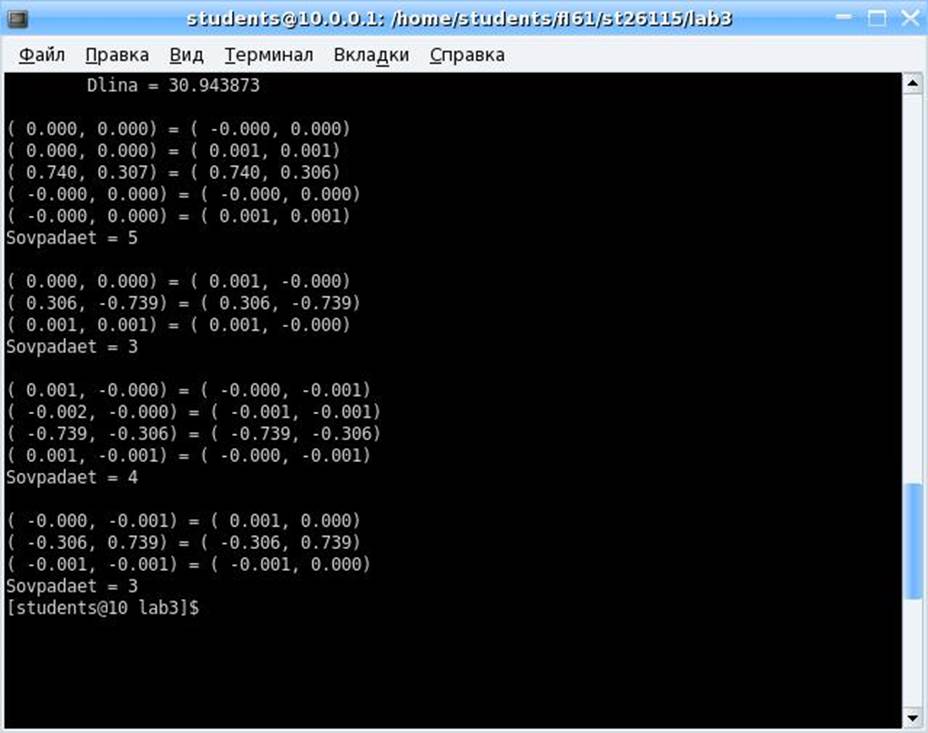
2.
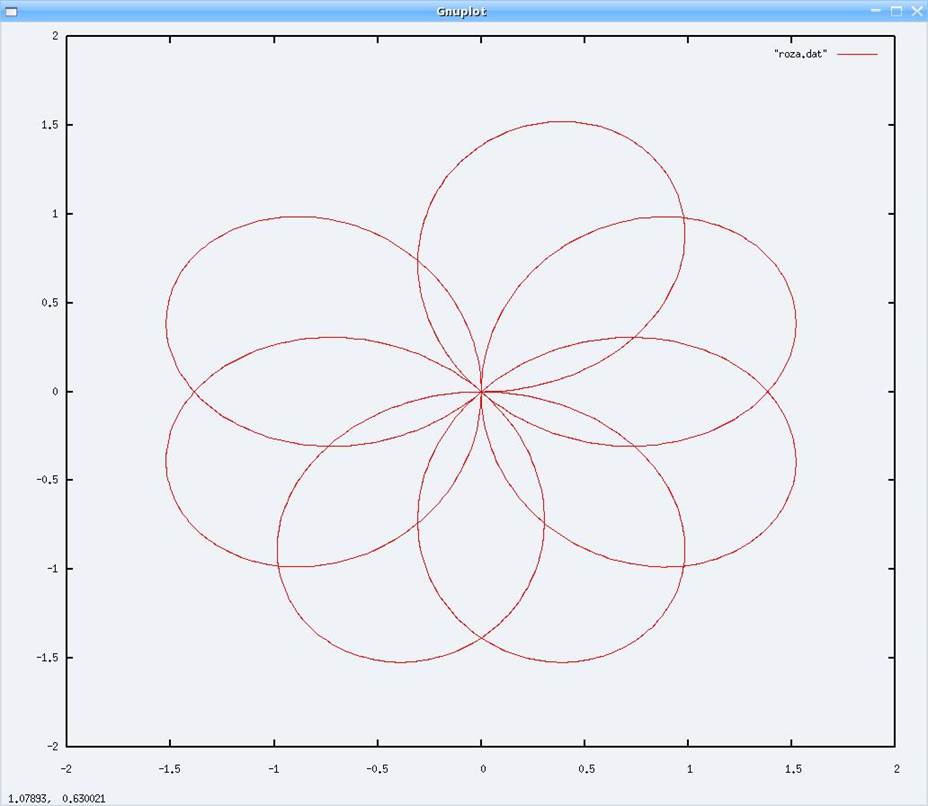 Произвели отрисовку графика розы по
точкам в программе gnuplot.
Произвели отрисовку графика розы по
точкам в программе gnuplot.
Описание программы
Список функций:
1. ro – подсчет радиус-вектора для перехода из полярной в декартову систему координат.
2. ro2 – подсчет производной функции ro.
3. dlina – расчет длины дуги посредством вычисления интеграла.
4. korni – данная функция предназначена для нахождения и подсчета точек пересечения нечетных лепестков.
Блок-схема программы
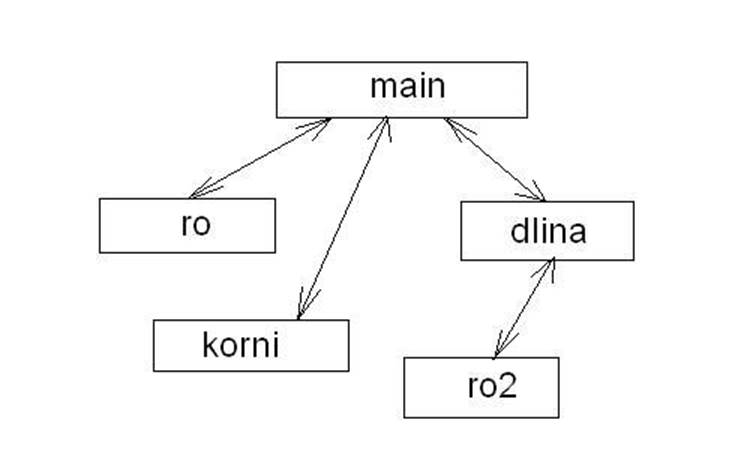
Приложение (текст программы)
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#define pi 3.1415
#define eps 0.2145*1e-4
#define e1 1e-5
double ro(double t)
{ return 1.6*sin(4.0*t/3); }
double ro2(double t)
{ return 1.6*cos(4.0*t/3)*4.0/3; }
double fun2(double t)
{ return sin(pi*t*t/2); }
double dlina(double x)
{
double x0=0,x1=x;
int i=0,n=50; double h,s1=0,s2=0;
do{
if (s2!=0) n*=2;
h=x1/n;
s2=s1;
s1=0;
for (i=0;i<=n;i++)
{
s1+=h*pow(pow(ro(i*h),2)+pow(ro2(i*h),2),0.5);
}
if (s2==0) s2=s1+4*eps;
}
while(fabs(s2-s1)>3*e1);
return s1;
}
int korni(double b)
{
double i,x1,y1,x2,y2,j; int k=0,n;
double di=0.001;
for (i=b; i<=b+3.0*pi/4;i+=di)
{
x1=ro(i)*cos(i);
y1=ro(i)*sin(i);
for (j=b;j<=b+3.0*pi/4;j+=di)
{
//x2=ro(j+1.5*pi)*cos(j+1.5*pi);
//y2=ro(j+1.5*pi)*sin(j+1.5*pi);
x2=ro(j+1.5*pi)*sin(j);
y2=ro(j+1.5*pi)*(-1)*cos(j);
if (fabs(x1-x2)<0.001&&fabs(y1-y2)<0.001) { printf("\n( %1.3f, %1.3f) = ( %1.3f, %1.3f)",x1,y1,x2,y2); k++; }
}
}
return k;
}
int main(void)
{
double a=1.6,r1=0,r2=0,x1=0,x2=0,y1=0,y2=0,x0=3.0*(pi/4)*7,h=0;
int n=1000,i,j;
FILE *f1;
do
{
f1=fopen("roza.dat","w");
if (x2!=0) n*=2;
h=x0/n;
x2=x1;
y2=y1;
y1=0; x1=0;
for (i=0;i<=n;i++)
{
x1=ro(0+h*i)*cos(0+h*i);
y1=ro(0+h*i)*sin(0+h*i);
fprintf(f1,"%f %f\n",x1,y1);
}
if (y2==0) y2=y1+2*eps;
if (x2==0) x2=x1+2*eps;
fclose(f1);
r1=x2-x1; r2=y2-y1;
}
while(fabs(r1)>3*eps&&fabs(r2)>3*eps);
printf("\n\tDlina = %f\n", dlina(3.0*(pi/4)*7));
for (j=0;j<4;j++)
printf ("\nSovpadaet = %d\n",korni(1.5*pi*j));
}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.