









Курсовая работа
по информатике
Факультет ФТФ
Группа ФЛ-61
Преподаватель Корель И.И
Студент Голобокова Л.С
Вариант 5
Новосибирск,2008
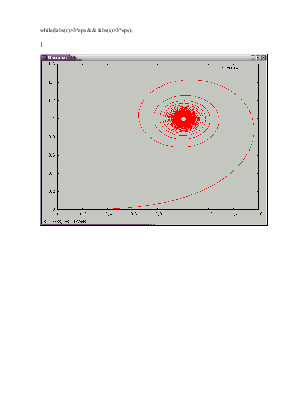
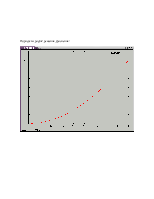
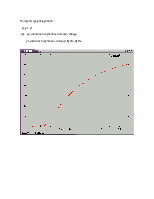
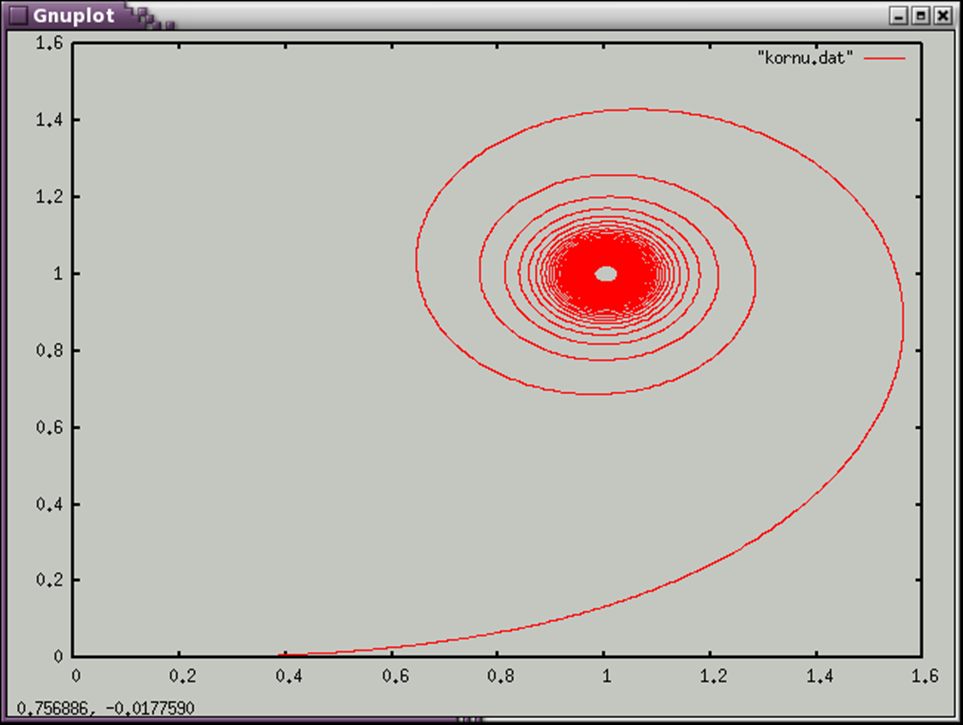
1 Нарисовать клофоиду( спираль Корню):
Найти пересечения клофоиды и функции у=а*х для произвольного а .
#include <stdio.h>
#include <math.h>
#define eps 1e-4
#define pi 3.1415
double fun1(double u)
{return cos(u*u*pi/2);}
double fun2(double u)
{return sin(u*u*pi/2);}
double pr(double x)
{
return x/2;
}
int main (void){
double h,l,x0=0,x1=28e0,sum1,sum2=0,sum11,sum22=0,r,s,a=1;
int i,n=2;
FILE *f1;
do{
f1=fopen("kornu.dat","w+");
if(sum2!=0) n*=2;
h=(x1)/n;
sum2=sum1;
sum22=sum11;
sum1=0;
sum11=0;
for(i=0;i<=n;i++)
{
sum1+=h*fun1(x0+i*h);//x
sum11+=h*fun2(x0+i*h);//y
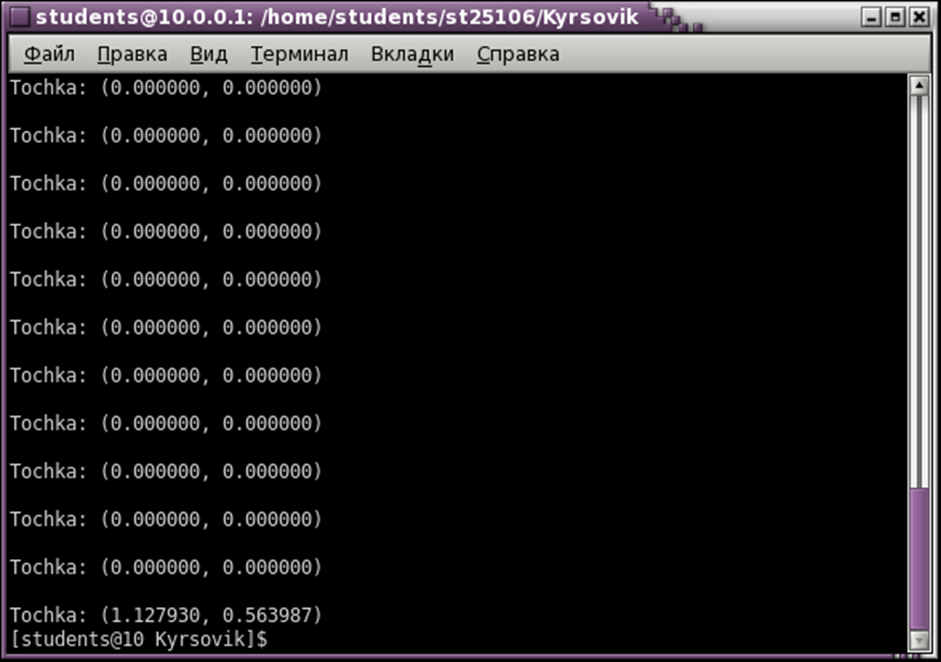
if (fabs(sum11-pr(x0+i*h))<eps) printf("\nTochka: (%f, %f)\n", x0+i*h,sum11);
fprintf(f1,"%f %f\n",a*sum1,a*sum11);
}
if(sum2==0) sum2=sum1+4*eps;
if(sum22==0) sum22=sum11+4*eps;
fclose(f1);
r=sum2-sum1;
s=sum22-sum11;
}
while(fabs(r)>3*eps && fabs(s)>3*eps);
}
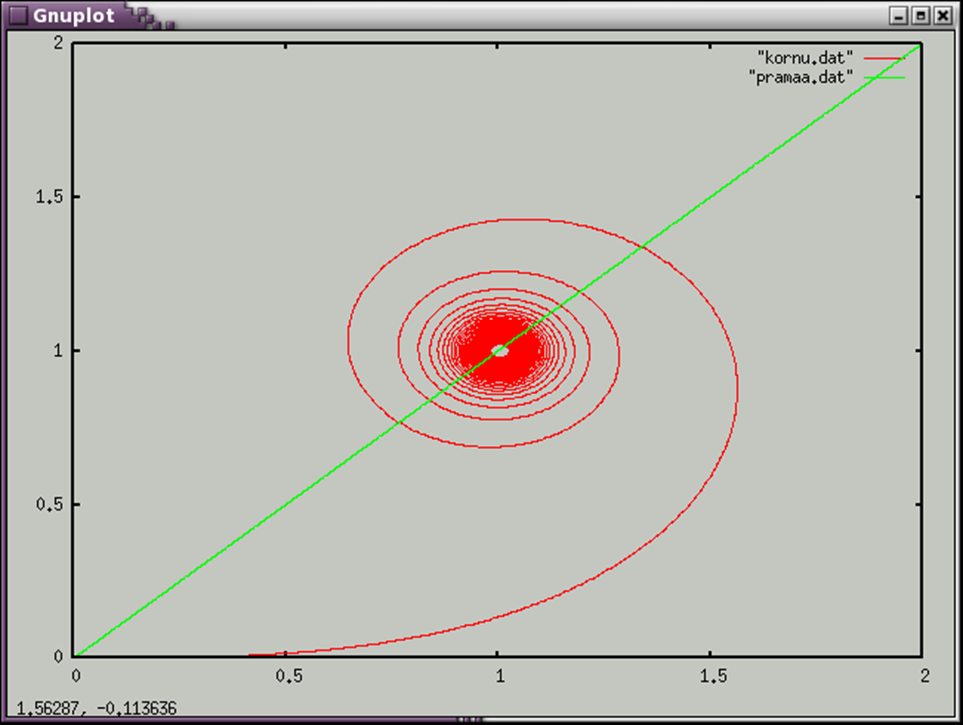
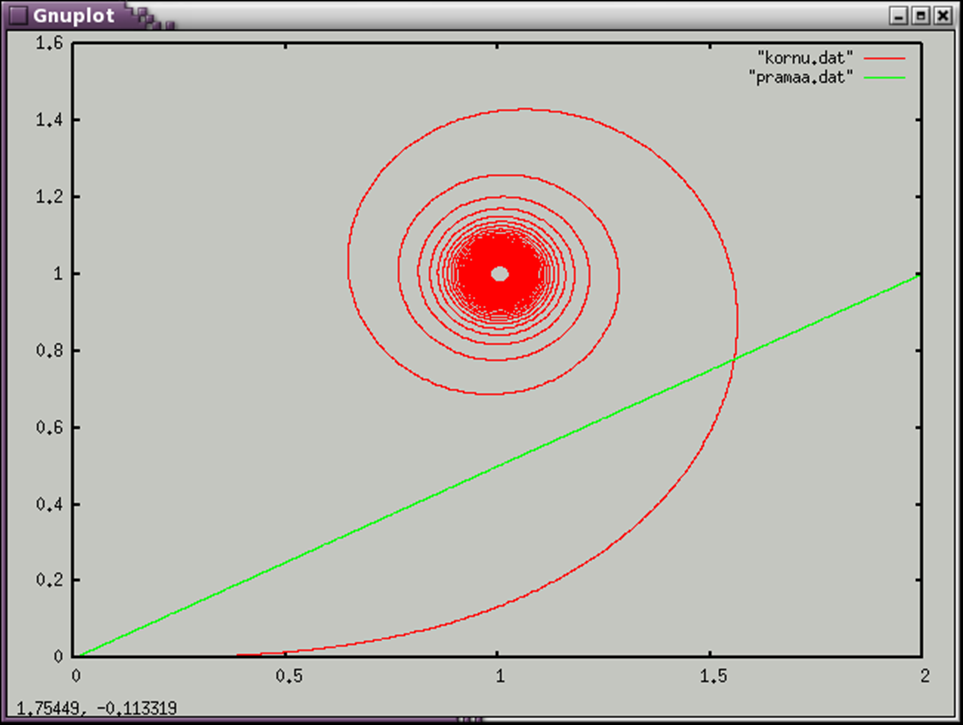
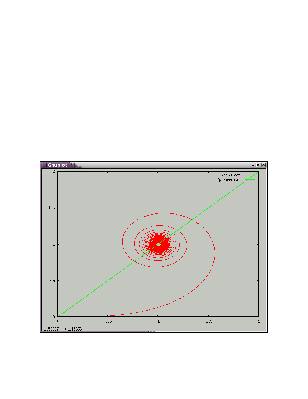
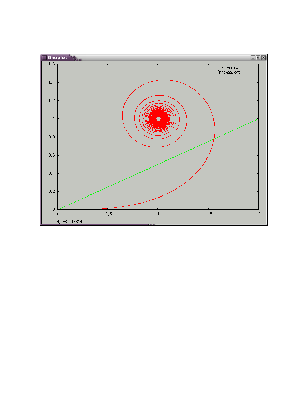
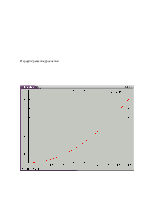
Найдем пересечение клофоиды с заданной прямой (рассмотрим частный случай,когда а=1/2
Используем метод дихотомии.
#include <stdio.h>
#include <math.h>
#define eps 1e-5
#define eps2 1e-7
#define pi 3.1415
double fun1(double u)
{return cos(u*u*pi/2);}
double fun2(double u)
{return sin(u*u*pi/2);}
double pr(double x)
{ return x/2; }
int main (void){
double h,l,x0=0,x1=28e0,sum1,sum2=0,sum11,sum22=0,r,s,a=1,A=0,B=1,xr;
int i,n=2;
FILE *f1;
do{
f1=fopen("kornut.dat","w+");
if(sum2!=0) n*=2;
h=(x1)/n;
sum2=sum1;
sum22=sum11;
sum1=0;
sum11=0;
for(i=0;i<=n;i++)
{
sum1+=h*fun1(x0+i*h);//x
sum11+=h*fun2(x0+i*h);//y
fprintf(f1,"%f %f\n",a*sum1,a*sum11);
xr=(A+B)/2 ;
if(sum1=(A+B)/2) {
if( sum11=A && (sum11-pr(A))*(sum11-pr(sum1))<0 ) A=sum1 ;
if( sum11=B && (sum11-pr(B))*(sum11-pr(sum1))<0) B=sum1 ;
}
}
if(sum2==0) sum2=sum1+4*eps;
if(sum22==0) sum22=sum11+4*eps;
fclose(f1);
r=sum2-sum1;
s=sum22-sum11;
}
while( (A-B)>=eps2);
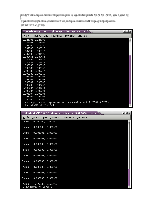
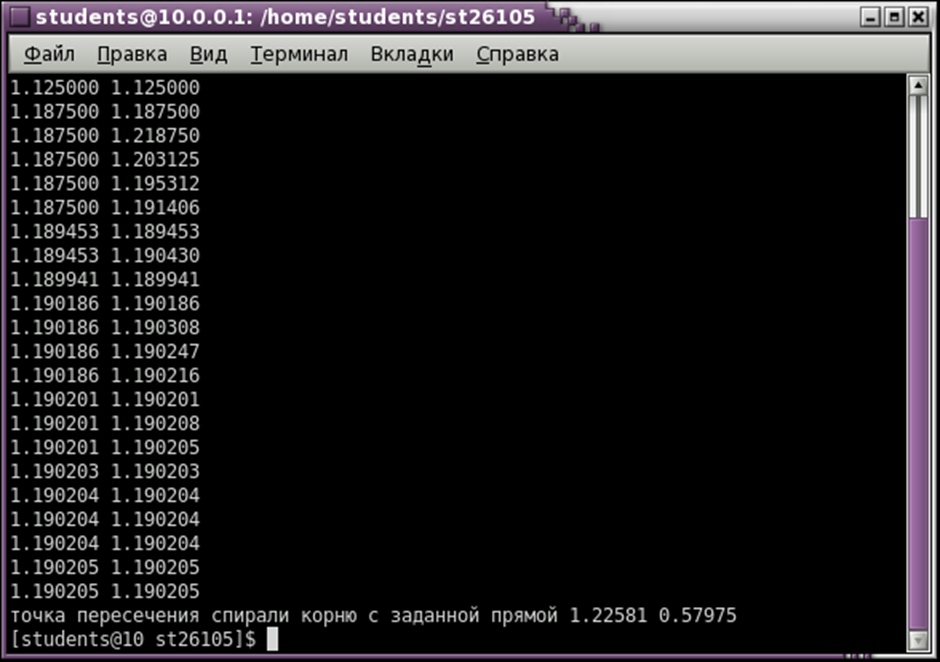
printf("точкa пересечения спирали корню с заданной кривой %1.5f %1.5f\n", sum1,sum11);
}
Сравним полученное значение с тем, которое можно найти сразу в программе
Ответ: x=1.2, y=0.6
1. Написать программу для приближенного интегрирования задачи Ко-
ши, используя методы Эйлера и Рунге-Кутты для:
(a) обыкновенного дифференциального уравнения
Метод Эйлера
Уравнение вида: 2xy'+y=2x^3
приведем к стандартному виду y'=F(x,y), т.е
y'=(2x^3-y)/2x
Текст программы:
#include <stdio.h>
#include <math.h>
#define eps 1e-2
double f(double x,double y)
{
return (2*x*x*x-y)/(2*x);
}
int main(void){
double x0=1.0,xn=2.0,y=0.0,y1=9/7,y2=0.0,h,x,r;
int n=1000000,i=0;
for (i=0;i<n;i++)
{
h=(xn-x0)/n;
if (y2!=0) { y1=y2; }
else y1=9/7;
y2=y1+h*(f(x0+i*h,y1)+f(x0+i*h,y1+h*f(x0+i*h,y1)))/2.0;
}
printf("Решение задачи Коши=%1.5f\n",y2);
}
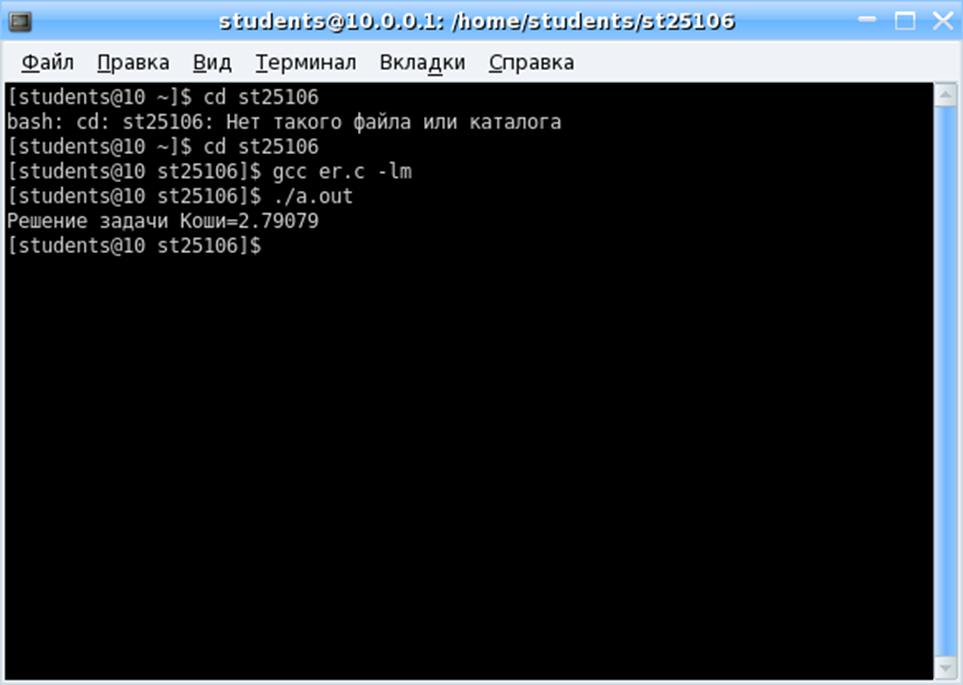
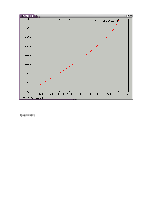
Нарисуем график решения уравнения:
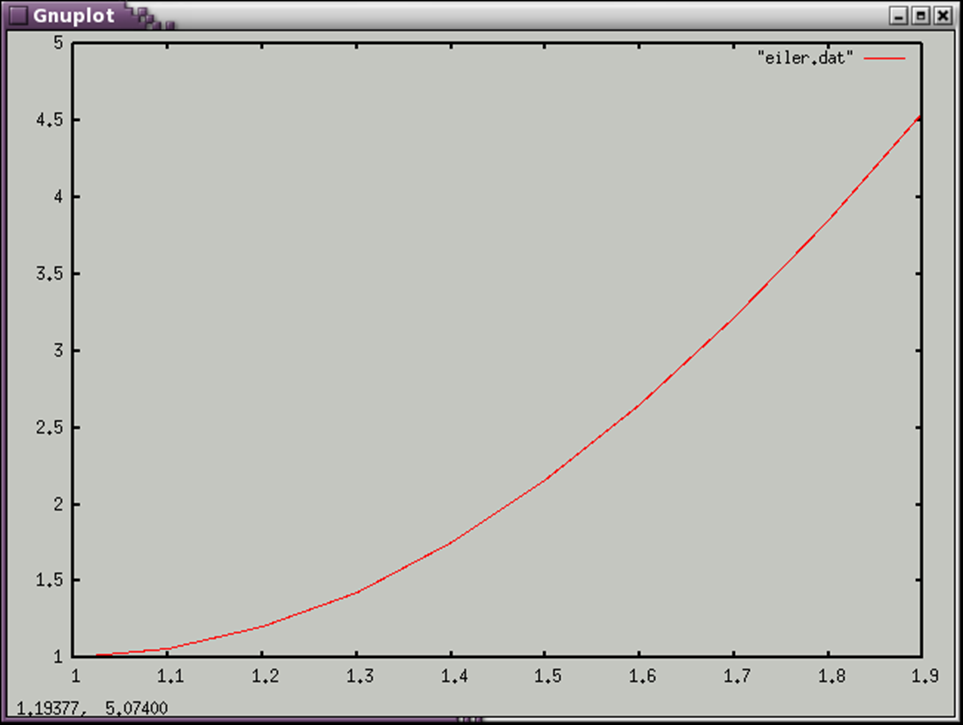
Метод Рунге-Кутте
#include <stdio.h>
#include <math.h>
#define eps 1e-2
double f(double x,double y)
{
return (2*x*x*x-y)/(2*x);
}
int main(void){
double x0=1.0,xn=2.0,y=0.0,y1=9/7,y2=0.0,h,x,r,k1,k2,k3,k4;
int n=100000,i=0;
for (i=0;i<n;i++)
{
h=(xn-x0)/n;
if (y2!=0) { y1=y2; }
else y1=9/7;
//printf("%d\n",n);
y2=y1+(k1+2*k2+2*k3+k4)/6;
k1=h*f(x0+i*h,y1);
k2=h*f(x0+i*h+h/2,y1+k1/2);
k3=h*f(x0+i*h+h/2,y2+k1/2);
k4=h*f(x0+i*h+h,y1+k3/2);
r=y2-y1;
}
printf("Решение задачи Коши=%1.5f\n",y2);
}
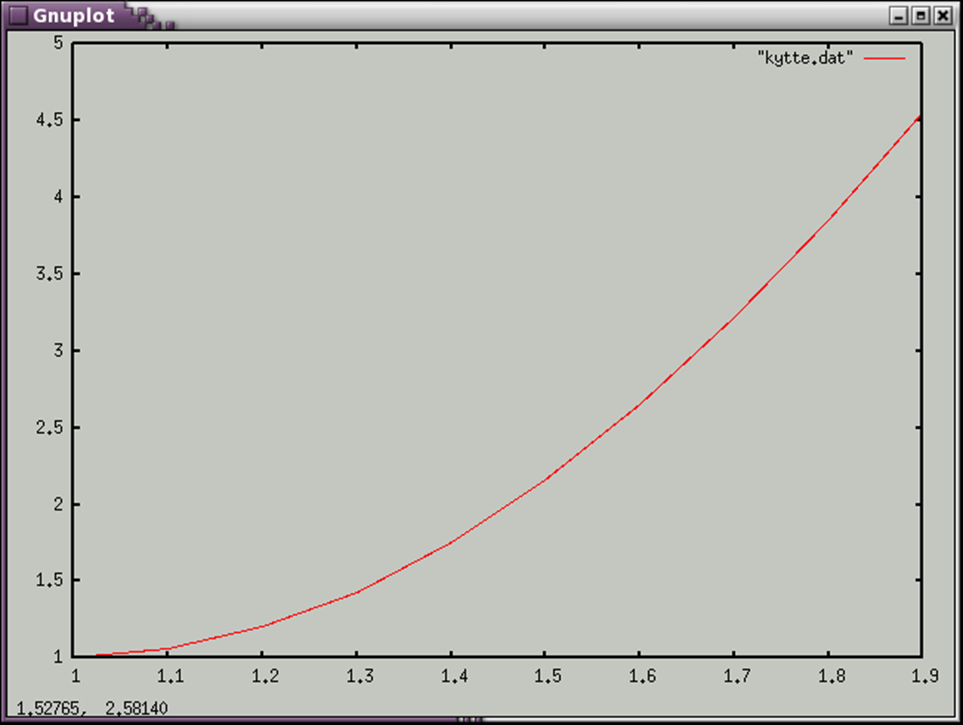
И график решения уравнения:
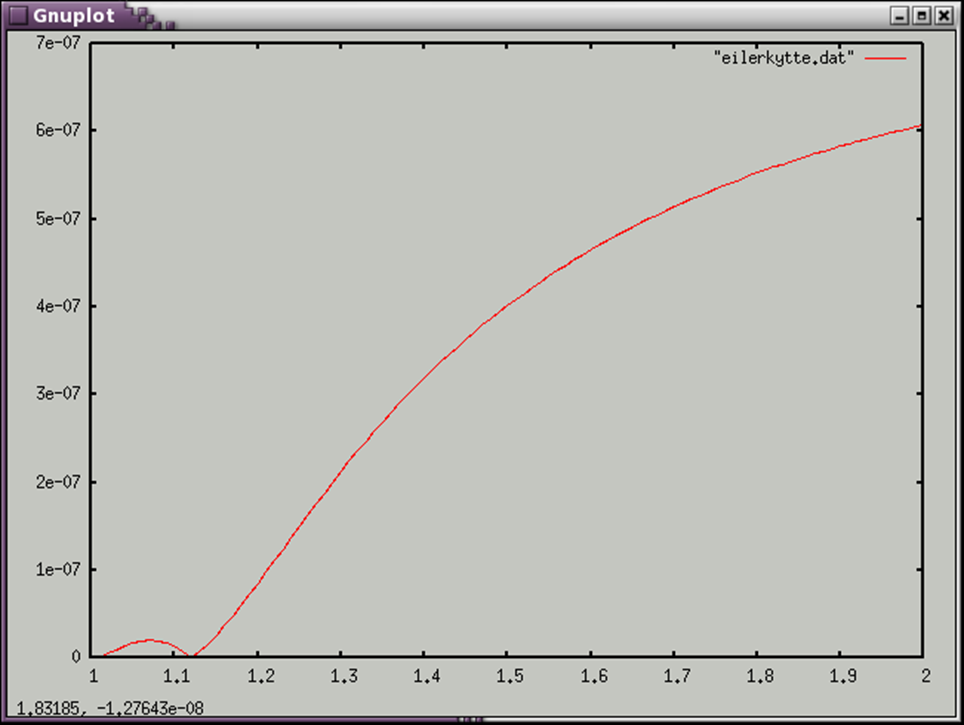
Построим график,который наглядно покажет ошибку двух способов решения уравнения.
Текст необходимой программы:
#include <stdio.h>
#include <math.h>
#define eps 1e-2
double f(double x,double y)
{
return (2*x*x*x-y)/(2*x);
}
int main(void){
FILE *EK;
EK=fopen("eilerkytte.dat","w+");
double x0=1.0,xn=1.0,yk=0.0,y1k=9/7,y2k=0.0,h,k1,k2,k3,k4,l;
double ye=0.0,y1e=9/7,y2e=0.0;
int n=1000000,i=0;
while(xn<=2)
{
for (i=0;i<n;i++)
{
h=(xn-x0)/n;
if (y2k!=0) { y1k=y2k; y2k=0; }
else y1k=1;
y2k=y1k+(k1+2*k2+2*k3+k4)/6;
k1=h*f(x0+i*h,y1k);
k2=h*f(x0+i*h+h/2,y1k+k1/2);
k3=h*f(x0+i*h+h/2,y2k+k1/2);
k4=h*f(x0+i*h+h,y1k+k3/2);
if (y2e!=0) { y1e=y2e; y2e=0; }
else y1e=1;
y2e=y1e+h*(f(x0+i*h,y1e)+f(x0+i*h,y1e+h*f(x0+i*h,y1e)))/2.0;
//xn+=0.01;
l=fabs(y2e-y2k)/fabs(y2k);
}
xn+=0.01;
fprintf(EK," %e %e\n",xn,l);
}
fclose(EK);
}
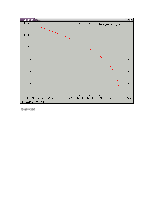
Построим график функции :
|ye-yr|/|yr|
,где ye- значение полученное методом Эйлера
yr-значение полученное методом Рунге-Кутта|
1. Написать программу для приближенного интегрирования задачи Ко-
ши, используя метод Рунге-Кутты для:
(b) системы ОДУ
#include <stdio.h>
#include <math.h>
#define eps 1e-2
double f1(double x,double y)
{
return 2*x;
}
double f2(double x,double y)
{
return 3*x-2*y;
}
double f3(double y,double z)
{
return 2*y+z;
}
int main(void){
FILE *DF;
DF=fopen("sistema2.dat","w");
double xn=4.0,x0=4.0,yx=0.0,yx1=1.0,yx2=0.0,h,x,r,k1,k2,k3,k4;
double yn=8.0,y0=8.0,yy=0.0,yy1=1.0,yy2=0.0,l1,l2,l3,l4;
double zn=-7.0,z0=-7.0,yz=0.0,yz1=1.0,yz2=0.0,m1,m2,m3,m4;
int n=1000000,i=0;
while(xn<=20 && yn<=20 && zn<=20)
{
for (i=0;i<n;i++)
{
h=(xn-x0)/n;
if (yx2!=0) { yx1=yx2; yx2=0; }
else yx1=4;
if (yy2!=0) { yy1=yy2; yy2=0; }
else yy1=8;
if (yz2!=0) { yz1=yz2; yz2=0; }
else yz1=-7;
yx2=yx1+(k1+2*k2+2*k3+k4)/6;
k1=h*f1(x0+i*h,yx1);
k2=h*f1(x0+i*h+h/2,yx1+k1/2);
k3=h*f1(x0+i*h+h/2,yx2+k1/2);
k4=h*f1(x0+i*h+h,yx1+k3/2);
yy2=yy1+(k1+2*k2+2*k3+k4)/6;
k1=h*f2(x0+i*h,yy1);
k2=h*f2(x0+i*h+h/2,yy1+k1/2);
k3=h*f2(x0+i*h+h/2,yy2+k1/2);
k4=h*f2(x0+i*h+h,yy1+k3/2);
yz2=yz1+(k1+2*k2+2*k3+k4)/6;
k1=h*f3(x0+i*h,yz1);
k2=h*f3(x0+i*h+h/2,yz1+k1/2);
k3=h*f3(x0+i*h+h/2,yz2+k1/2);
k4=h*f3(x0+i*h+h,yz1+k3/2);
}
fprintf(DF,"%f %f %f\n",yx2,yy2,yz2);
xn+=0.1;
yn+=0.1;
zn+=0.1;
}
printf("РешениезадачиКоши=%1.5f %1.5f %1.5f\n",yx2,yy2,yz2);
fclose(DF);
}
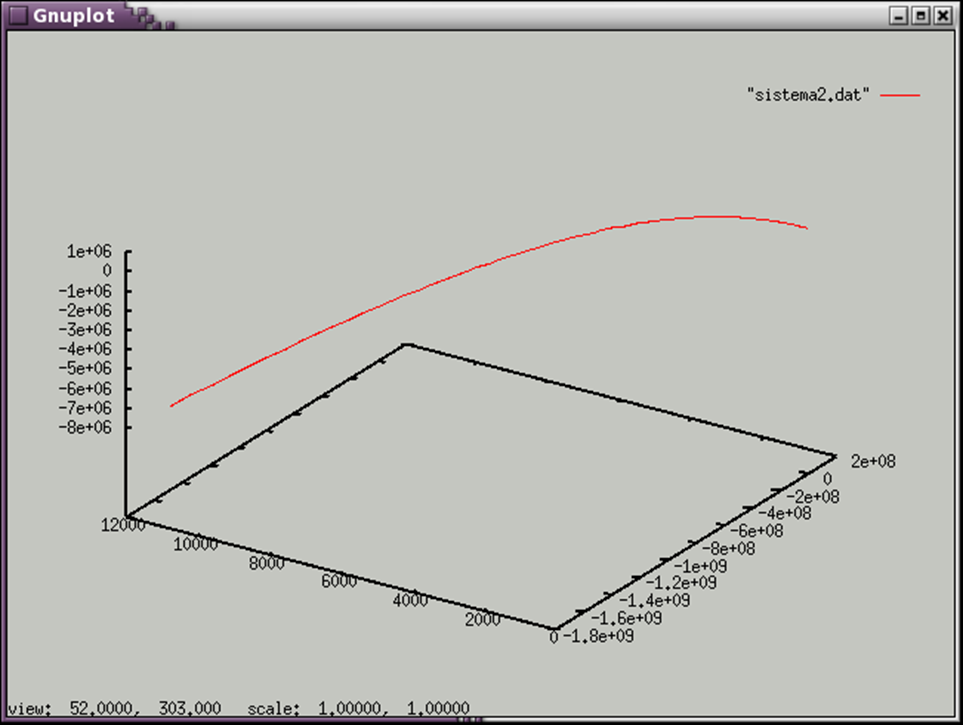
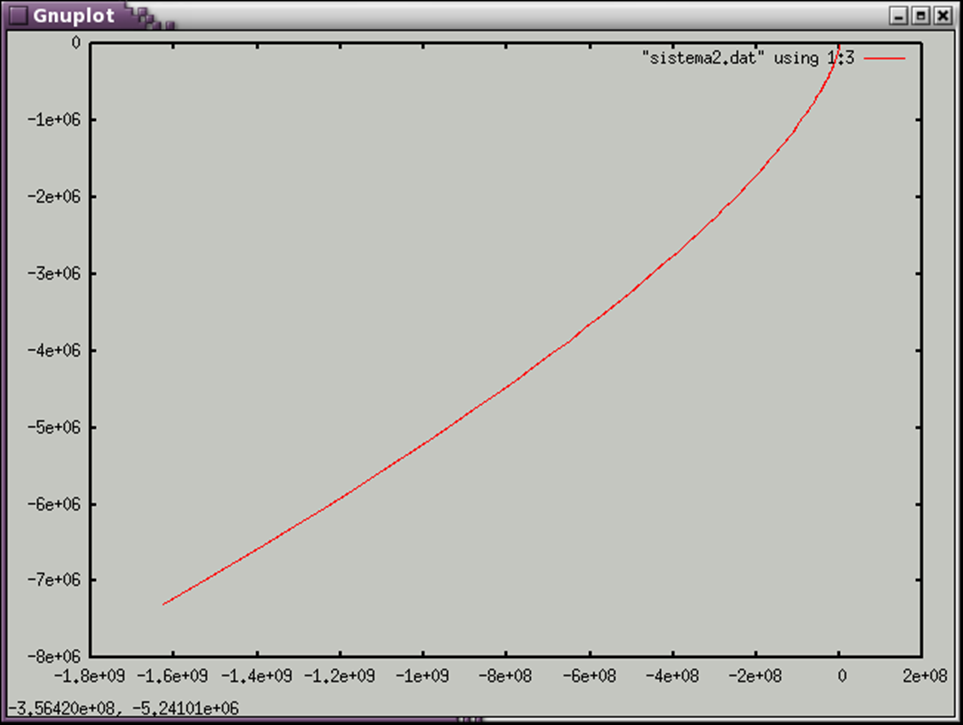
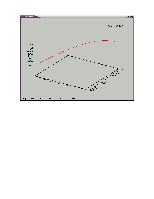
График Z(x)
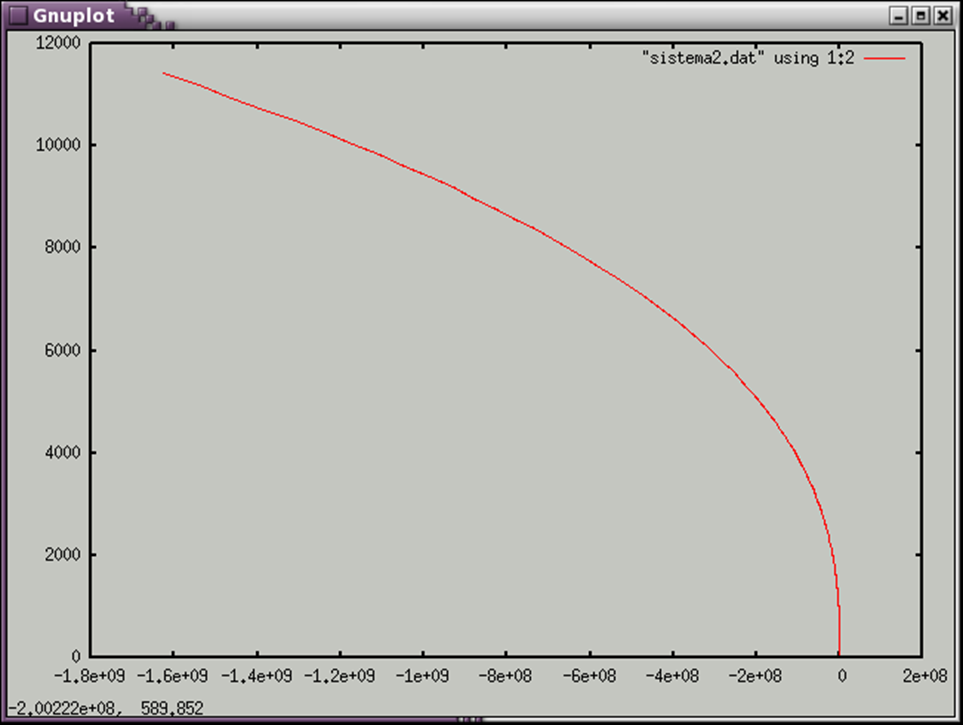
График y(x)
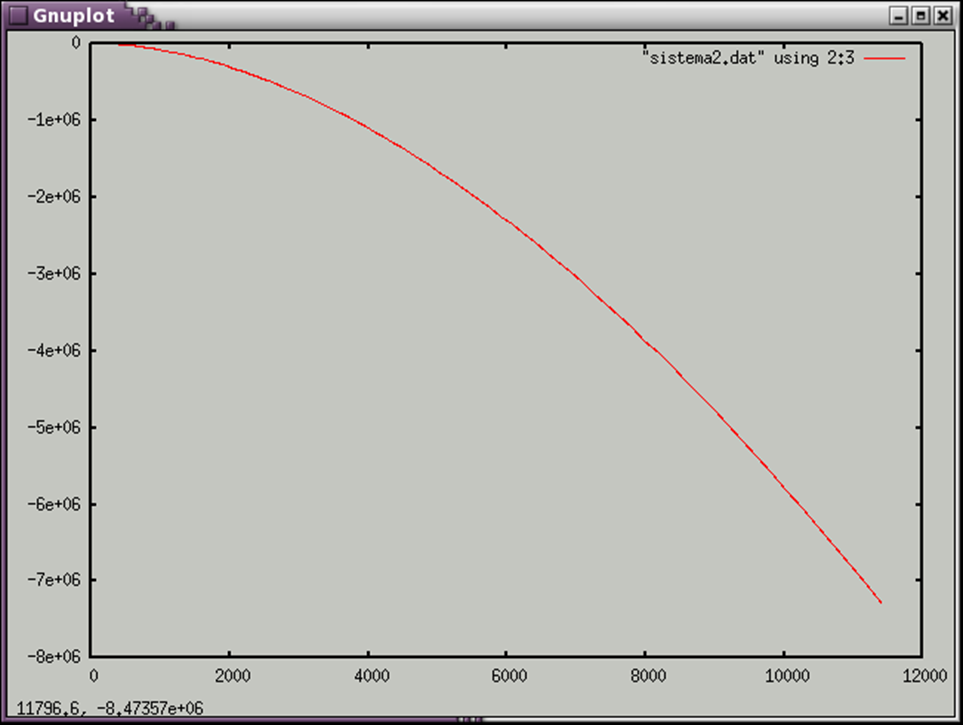
График z(y)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.