Курсовая работа
по информатике
Факультет ФТФ
Группа ФЛ-71
Студент Алюкаева О.З.
Преподаватель Корель И.И.
Новосибирск,2009
1 Нарисовать гиперболическую спираль: ρ = a/φ , a = 2.7. Найти длину
спирали φ ∈ [0.1, 5.7]. Найти её пересечения с окружностью единичного радиуса.
Текст програмы:
#include <stdio.h>
#include <math.h>
#define a 2.7
double fun (double f){
return a/f;}
double dfun(double f)
{return -a/(f*f);}
double X(double f){
return a*cos(f)/f;}
double Y(double f)
{return a*sin(f)/f;}
int main (void)
{double l=0.0,f,b1,b2,r1,r2,df;
b1=0.1;
b2=5.7;
f=b1;
df=0.0001;
FILE *DF;
DF=fopen("kurs.dat","w");
while (f<b2){
r1=fun(f);
r2=dfun(f);
l=l+sqrt(r1*r1+r2*r2)*df;
fprintf(DF,"%e %e\n",X(f),Y(f));
f+=df;
if (fabs(Y(f)-sqrt(1-X(f)*X(f)))<0.00001) printf("(%f,%f)\n",X(f),Y(f));}
fclose(DF);
printf("\nDlina spirali=%f\n",l);}
Графики:
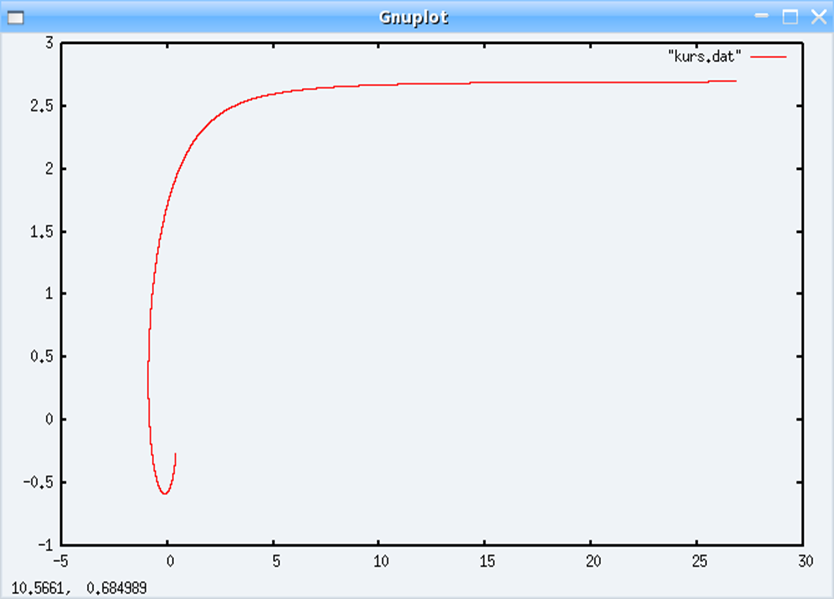
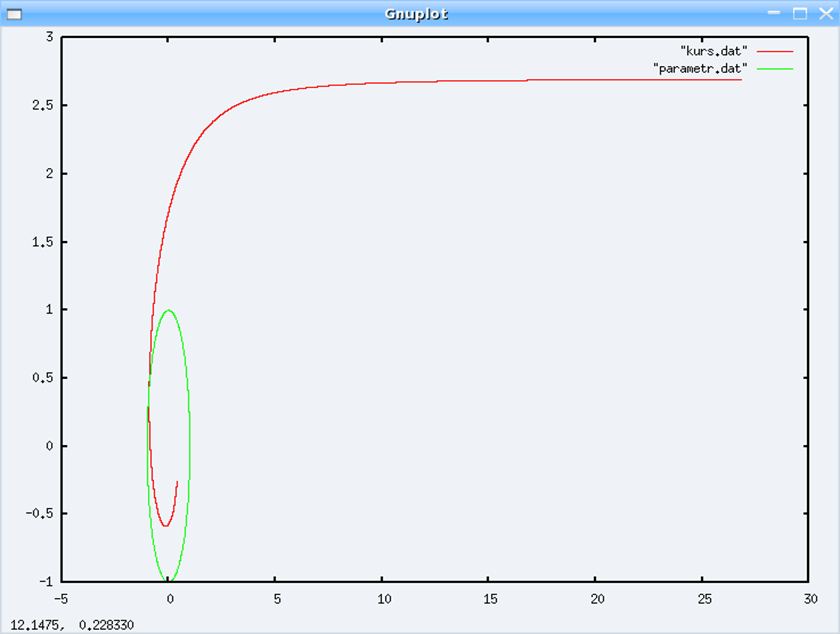

Получаем ответ:
Точка пересечения имеет координаты (-0.904072,0.427380)
Длина спирали равна 30.728720
1. Написать программу для приближенного интегрирования задачи Ко-
ши, используя методы Эйлера и Рунге-Кутты для:
(a) обыкновенного дифференциального уравнения
Метод Эйлера
Уравнение вида: y'+у*tan(x)=sin(2x)
приведем к стандартному виду y'=F(x,y), т.е
y'=sin(2x)-y*tan(x)
Текст программы:
# include <stdio.h>
# include <math.h>
double fun (double x, double y){
return sin(2*x)-y*tan(x);}
int main (void){
double a, b, n, h, x1, x2, y1, y2;
a=0;
b=2;
n=1500;
h=(b-a)/n;
x1=0;
y1=2;
FILE *DF;
DF=fopen("ky2.dat","w");
while (x1<b){ x2=x1+h;
y2=y1+h*(fun(x1,y1)+fun(x2,y1+h*fun(x1,y1)))/2.0;
fprintf(DF,"%e %e \n",x2,y2);
x1=x2;
y1=y2;}
fclose(DF);}
График решения уравнения:
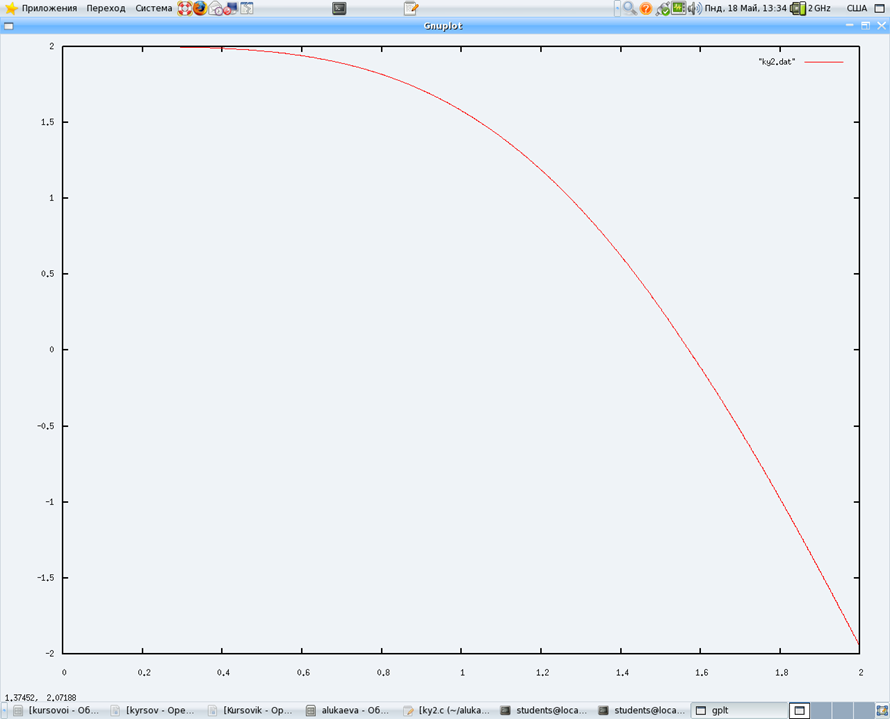
Метод Рунге-Кутте
Текст программы:
# include <stdio.h>
# include <math.h>
double fun (double x, double y){
return sin(2*x)-y*tan(x);}
int main (void){
double a, b, n, h, x1, x2, y1, y2, k1, k2, k3, k4;
a=0;
b=2;
n=1500;
h=(b-a)/n;
x2=0;
y2=2;
FILE *DF;
DF=fopen("ky.dat","w");
while (x1<b){ x1=x2+h;
k1=fun(x2,y2)*h;
k2=fun(x2+h/2.0,y2+k1/2.0)*h;
k3=fun(x2+h/2.0,y2+k2/2.0)*h;
k4=fun(x2+h/2.0,y2+k3/2.0)*h;
y1=y2+(k1+2.0*k2+2.0*k3+k4)/6;
fprintf(DF,"%e %e \n",x1,y1);
x2=x1;
y2=y1;}
fclose(DF);}
График решения уравнения:
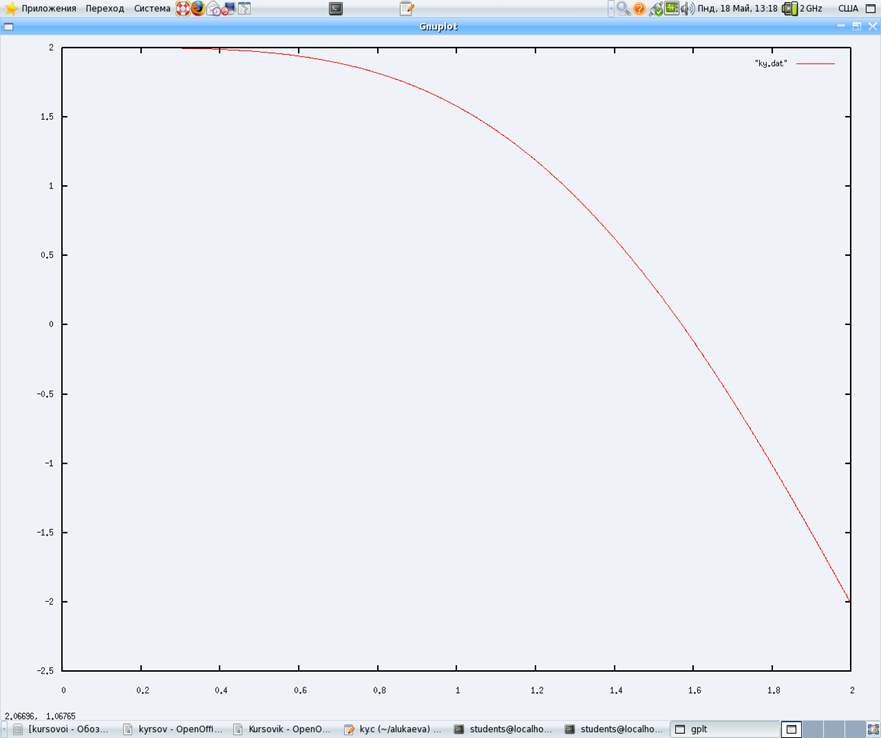
(b) Написать программу для вычисления системы дифференциальных уравнений методом Рунге-Кутта.
Дано: система
x'=2*x
y'=3*x-2*y
z'=2*y+z
Начальные условия (4,8,-7)
отрезок [0;10]
Текст программы:
# include <stdio.h>
# include <stdlib.h>
# include <math.h>
double fun1 (double t, double x){
return 2*x;}
double fun2 (double t, double x, double y ){ return 3*x-2*y;}
double fun3 (double t, double y, double z){ return 2*y+z;}
int main (void){ double t0, k11, k12, k13, k14, k21, k22, k23, k24, k31, k32, k33, k34, xk, yk, zk, n, h, i,t;
double xk1, yk1, zk1;
t0=0; k11=0; k12=0; k13=0; k14=0; k21=0; k22=0; k23=0; k24=0; k31=0; k32=0; k33=0;k34=0;
xk=4;
yk=8;
zk=-7;
n=100;
h=(10)/n;
i=0;
FILE *DF;
DF=fopen("sis.dat", "w");
for (i=0; i<=n; i++){ t=t0+i*h;
k11=fun1(t,xk)*h;
k12=fun1(t+h/2.0, xk+k11/2.0)*h;
k13=fun1(t+h/2.0, xk+k12/2.0)*h;
k14=fun1(t+h,xk+k13)*h;
xk1=xk+(k11+2.0*k12+2.0*k13+k14)/6.0;
k21=fun2(t,xk,yk)*h;
k22=fun2(t+h/2.0, xk+k21/2.0, yk+k21/2.0)*h;
k23=fun2(t+h/2.0, xk+k22/2.0, yk+k22/2.0)*h;
k24=fun2(t+h,xk+k23,yk+k23)*h;
yk1=yk+(k21+2.0*k22+2.0*k23+k24)/6.0;
k31=fun3(t,yk,zk)*h;
k32=fun3(t+h/2.0, yk+k31/2.0, zk+k31/2.0)*h;
k33=fun3(t+h/2.0, yk+k32/2.0, zk+k32/2.0)*h;
k34=fun3(t+h,yk+k33,zk+k33)*h;
zk1=zk+(k31+2.0*k32+2.0*k33+k34)/6.0;
fprintf(DF,"%e %e %e\n",xk1,yk1,zk1);
xk=xk1;
yk=yk1;
zk=zk1; }
fclose(DF);}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.