Задача 2,2
Оценить надежность ДПТ при экспоненциальном законе распределения отказов его элементов. Рассчитать вероятность безотказной работы за время 500, 1000, 2000, 5000 часов. Построить зависимость Р(t) и определить среднее время безотказной работы Тср.
Исходные данные (В–32):
Интенсивность отказа λ∙10-4, час-1:
– λобм = 1,7 обмотки;
– λподш = 1 подшипников;
– λщку = 1,2 щеточно-коллекторного узла;
– λцбр = 1 центробежного регулятора.
Решение
ДПТ разбивается на следующую схему:

Результирующая вероятность при последовательной структуре:
РДПТ(t) = Робм(t) ∙
Рподш(t) ∙ Рщку(t) ∙ Рцбр(t) = ![]() ,
,
где λΣ = λобм + λподш + λщку + λцбр,
λΣ = (1,7 + 1 + 1,2 +1)∙10-4 = 4,9∙10-4,
РДПТ(500) = ![]() .
.
Остальные вероятности для других промежутков времени сведены в таблицу 1.
Таблица 1 – Вероятность безотказной работы за время t
|
t, час |
500 |
1000 |
2000 |
5000 |
|
РДПТ |
0,782705 |
0,612626 |
0,375311 |
0,086294 |
По данным таблицы 1 построена зависимость РДПТ(t) (см. рисунок 1).
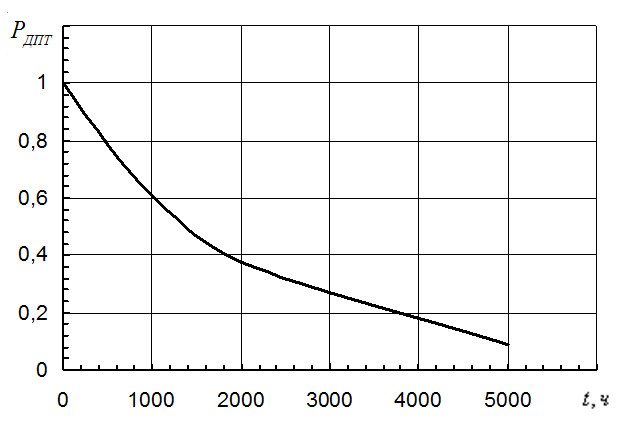
Рисунок 1 – Зависимость РДПТ = f(t).
Среднее время безотказной работы, Тср, час,
ТСР = 1/λΣ,
ТСР = 1/(4,9∙10-4) = 2040,816.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.