• Кількість респондентів, які не відповіли на це питання (Missing: N = 19, Percent = 0,6%). Анкета розглядується як відсутнє спостереження (Missing, НеВідп), якщо жодна зі змінних набору не має значення, що враховується (у нашому прикладі значення "1").
• кількість анкет (Total: N = 3057; Percent = 100%).
Одновимірний розподіл представлено у таблиці $Р1 Frequencies
Основна інформація, тобто сам одномірний розподіл, міститься у таблиці $Р1 Frequencies. Приінтерпретації результатів треба пам’ятати, що ознака, яка нами аналізується, виміряна за допомогою номінальної шкали з сумісними альтернативами. Саме тому у рядку Total вказано 7256 (кількість виборів респондентами альтернатив відповідей на питання анкети), а не 3038 (кількість анкет, що аналізуються).
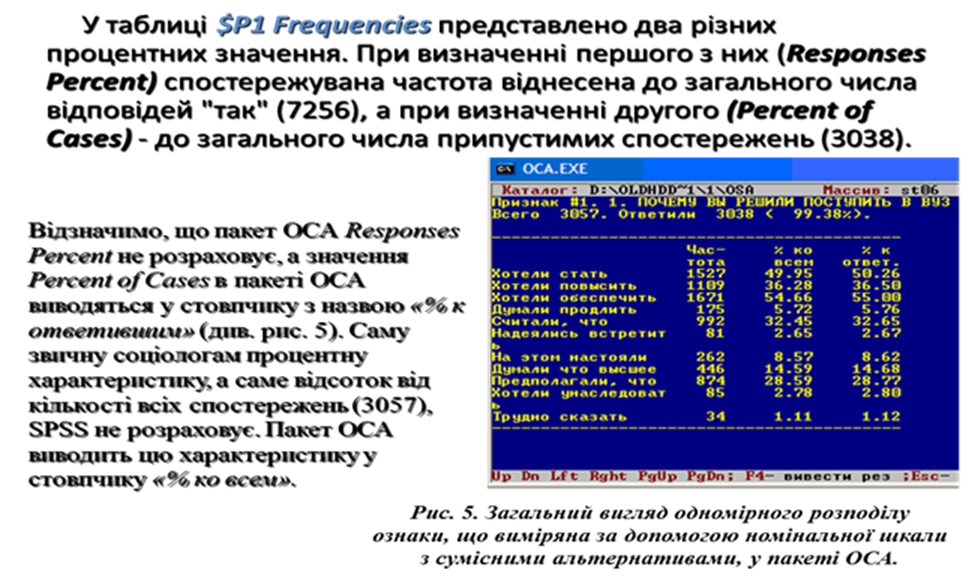
У таблиці $Р1 Frequencies представлено два різних процентних значення. При визначенні першого з них (Responses Percent) спостережувана частота віднесена до загального числа відповідей "так" (7256), а при визначенні другого (Percent of Cases) - до загального числа припустимих спостережень (3038).
Відзначимо, що пакет ОСА Responses Percent не розраховує, а значення Percent of Cases в пакеті ОСА виводяться у стовпчику з назвою «% к ответившим» (див. рис. 5). Саму звичну соціологам процентну характеристику, а саме відсоток від кількості всіх спостережень (3057), SPSS не розраховує. Пакет ОСА виводить цю характеристику у стовпчику «% ко всем».
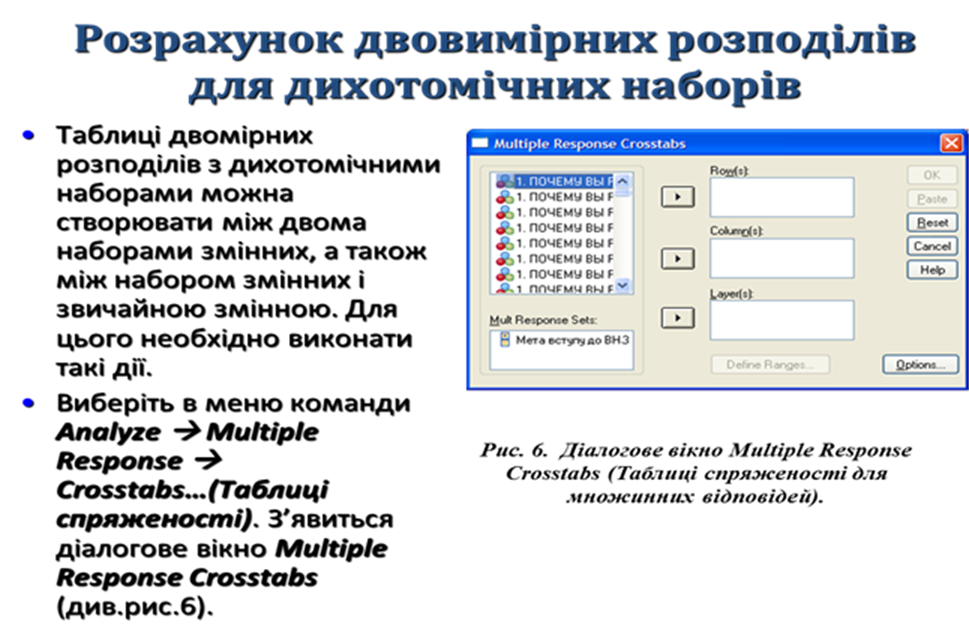
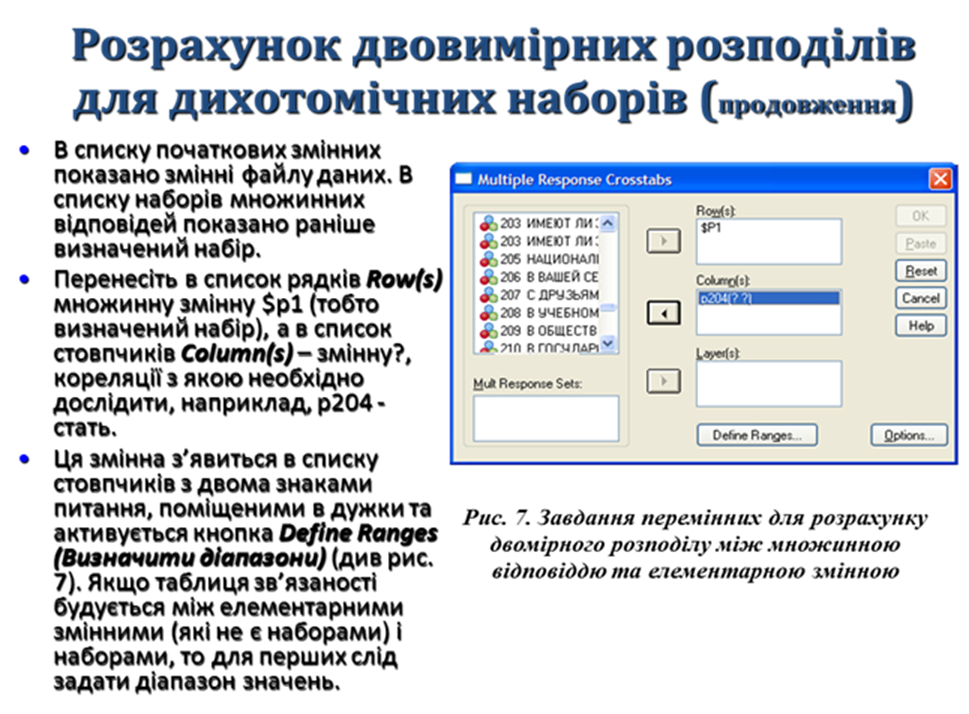
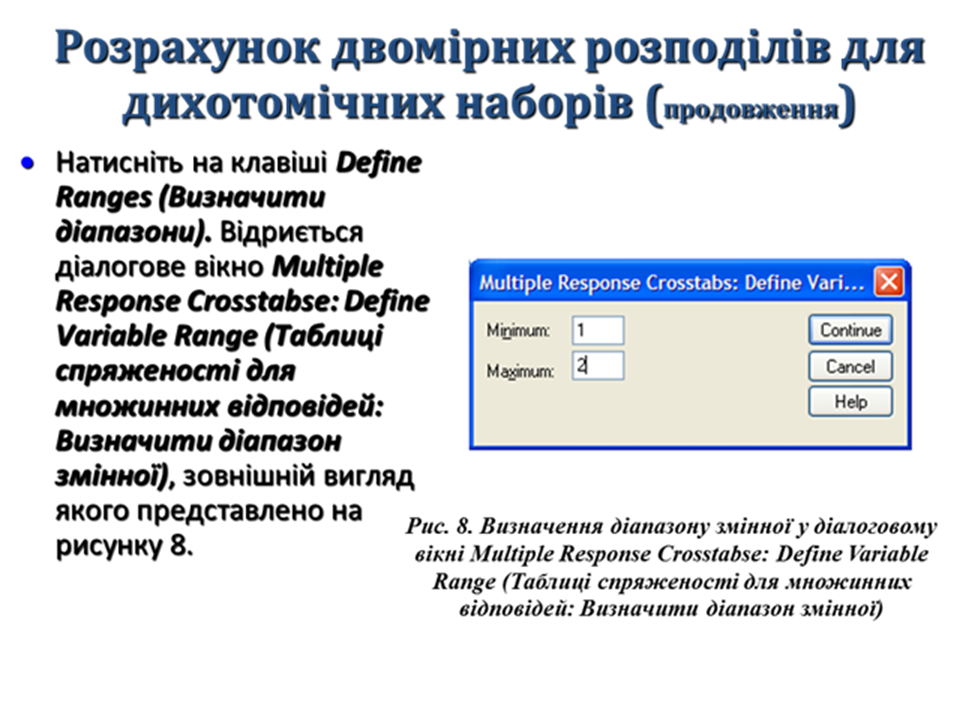
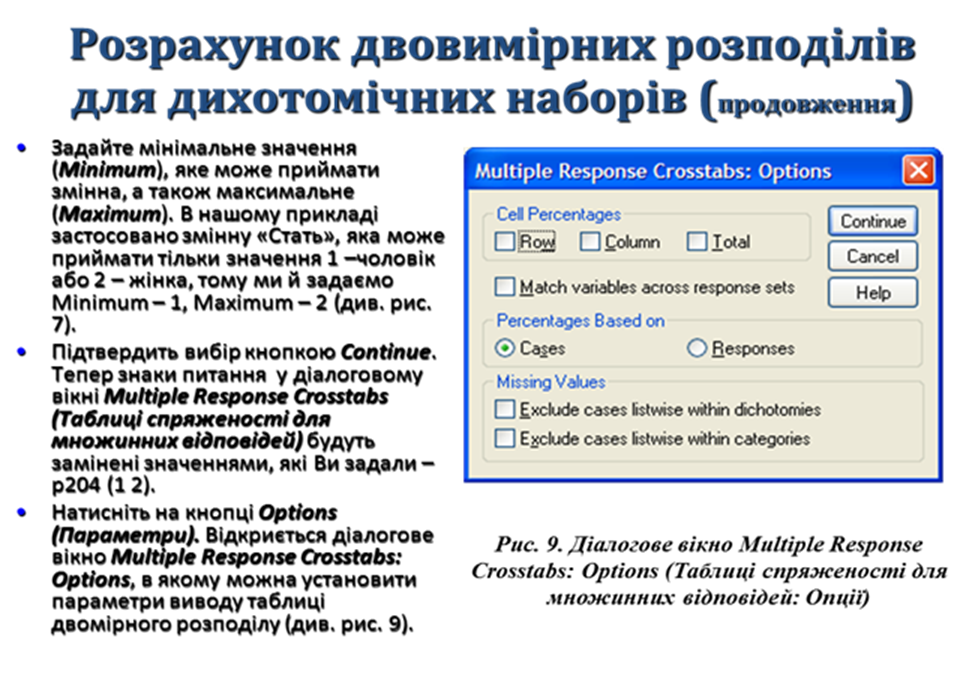
Результат розрахунку двовимірного розподілу множинної відповіді $р1 та ознаки р204.
Література
• Бююль А., Цёфель П. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей. – СПб.: ООО «ДиаСофтЮП», 2002. – С. 207-219.
Курс «Методи аналізу соціологічної інформації»
Лекция 8. Тема «Аналіз розбіжностей: сутність та застосування в соціологічних дослідженнях»
Курс «Методи
комп'ютерної обробки соціологічної інформації: ОСА, SPSS»
Тема Розрахунок значущості розбіжностей
відсотків (часток) в пакетах ОСА та SPSS»
План лекції
1. Аналіз розбіжностей та його застосування
2. Аналіз розбіжностей відсотків. Статистична значущість розбіжностей відсотків
3. Розрахунок розбіжностей відсотків (часток) у пакеті ОСА
4. Розрахунок розбіжностей відсотків (часток) у пакеті SPSS
3.Розрахунок значущості розбіжностей відсотків (часток) в пакеті ОСА
Приклад аналізу розбіжностей відсотків в пакеті ОСА:перевірка значущості розбіжностей в оцінках цінності сімейного благополуччя серед чоловіків і жінок (масив st09)
Наша змістовна гіпотеза полягає в тому, що для жінок сімейне благополуччя більш цінне, ніж для чоловіків. Статистична – що у двох групах респондентів, розподілених за ознакою 296 (стать), відрізняється розподіл ознаки 60 (цінність сімейного благополуччя).
Для перевірки даної гіпотези необхідно:
1) Побудувати два фільтри для відбору двох груп респондентів.
2) Підключити фільтри та побудувати одновимірні розподіли.
3) Перевірити наявність розбіжностей «на перший погляд» та, в разі наявності, перейти до перевірки їх статистичної значущості.
4) Скласти таблицю для порівняння результатів дослідження в двох групах.
5) Змістовно проінтерпретувати отримані результати.
1.Побудувати два фільтри для відбору двох груп респондентів.
Фільтр для відбору чоловіків - (#296#=1),
жінок – (#296#=2) 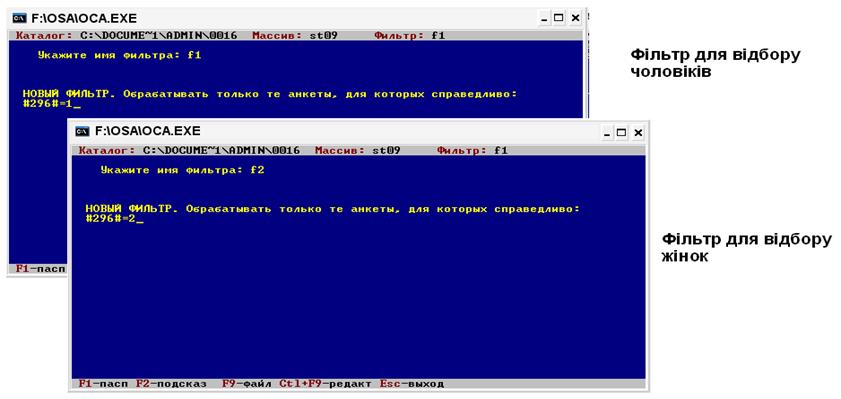
2.Підключити перший фільтр та побудувати одновимірний розподіл за ознакою «цінність сімейного благополуччя» серед чоловіків, потім підключити другий фільтр та розрахувати одновимірний розподіл за тією ж ознакою серед жінок.
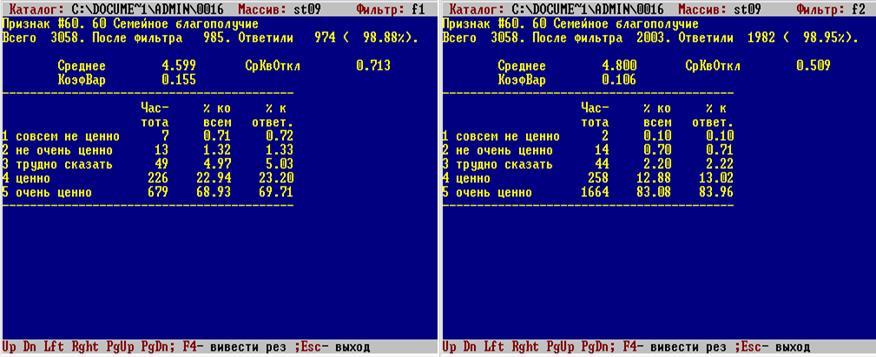
3. Перевірити наявність розбіжностей «на перший погляд». Якщо відмінності помітні, треба перейти до перевірки їх статистичної значущості.
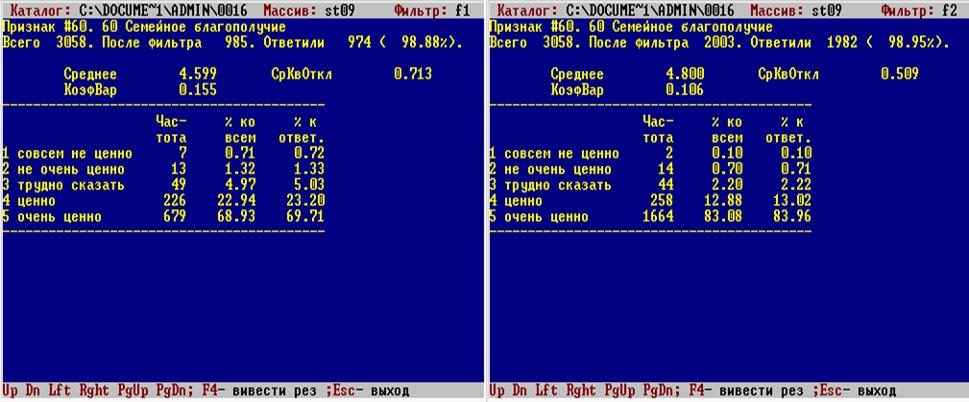
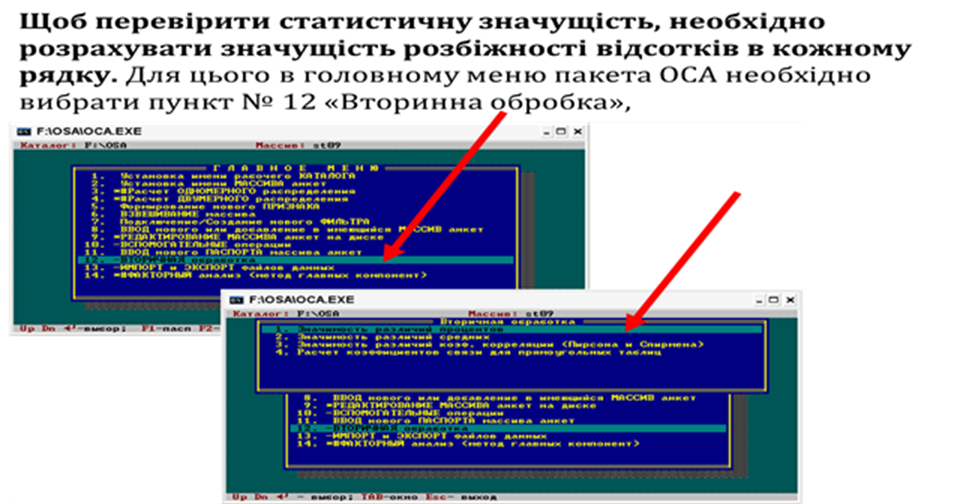
Для перевірки гіпотези необхідно вказати два значення відсотків (P1 і P2) та обсяги відповідних вибірок, для яких ці два відсотка було обчислено (n1 і n2)
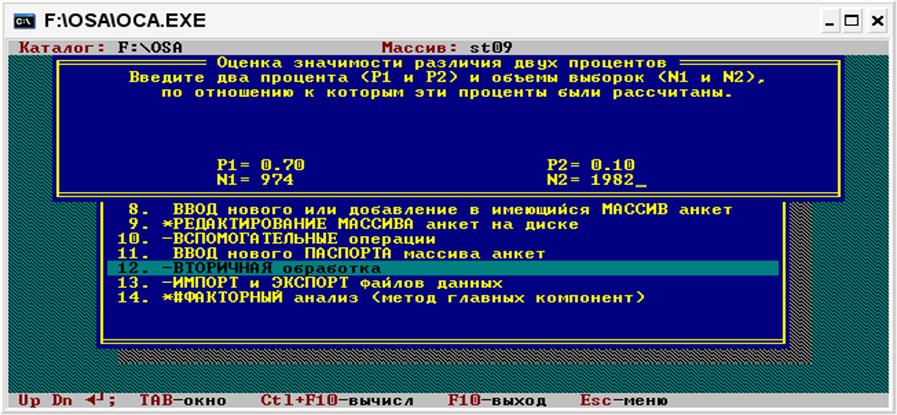
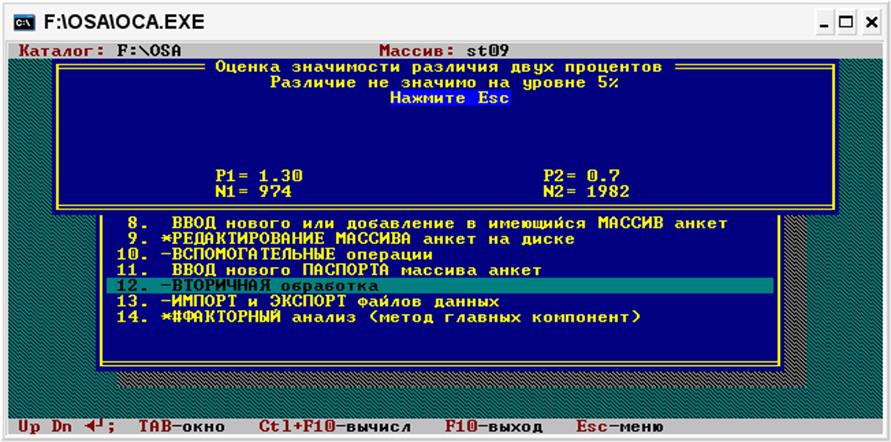
Щоб отримати результати розрахунків, необхідно натиснути комбінацію клавіш Ctrl+F10. Результат буде виглядати так, як представлено на рисунку.
Результат розрахунків, який представлено на рис., свідчить про неможливість обчислити значущість розбіжностей відсотків за тими формулами, що застосовуються пакетом ОСА. Проте це можна зробити вручну або із застосуванням іншого програмного засобу.
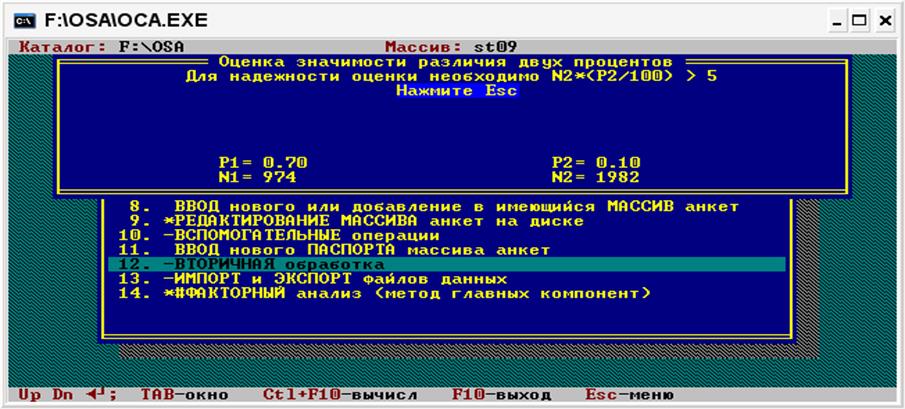
Якщо гіпотеза про відсутність розбіжностей не може бути відкинута на жодному із двох рівнів значущості (1% та 5%), то виводиться повідомлення «Розбіжність не значуща на рівні 5%».
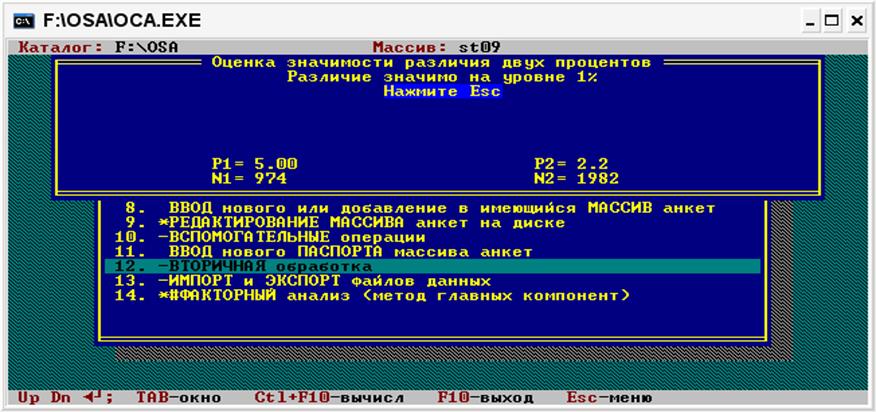
Якщо нульова гіпотеза може бути відкинута на одному із цих двох рівнів значущості, то виводиться повідомлення «Розбіжність значуща на рівні ...%» (у повідомленні вказується більш високий рівень значущості).
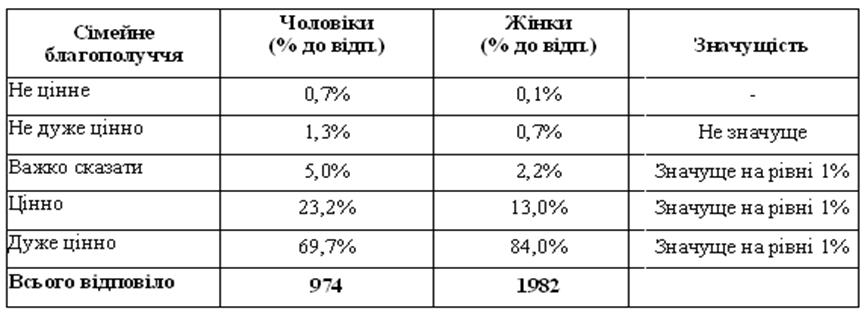
4. Для порівняння результатів дослідження в двох групах потрібно скласти таблицю, яка має містити також результати перевірки статистичної значущості.
5. Проінтерпретуйте результат! Які змістовні висновки Ви можете зробити? Чи можна в даному випадку застосовувати порівняння середніх? Що, на вашу думку, зручніше – порівнювати відсотки чи середні (середні: чоловіки – 4,599; жінки – 4,800)?
Не можна описувати та інтерпретувати відмінності, не перевіривши їх статистичну значущість, тому що це може призвести до помилки першого роду (див. тему «Перевірка статистичних гіпотез»). Змістовну інтерпретацію розбіжностей слід робити, враховуючи їх статистичну значущість та вказуючи її значення за умови представлення даних (приклад див. далі).
Приклад 1. Електорат парламентських виборів у демографічних вимірах (Джерело: Національний екзит-пол: парламентські вибори´2006. – К.: Центр «Демократичні ініціативи», 2006. – С. 43-46. – Режим доступу: http://old.dif.org.ua/modules/pages/files/Exit_ poll_2006_Ukr.pdf)
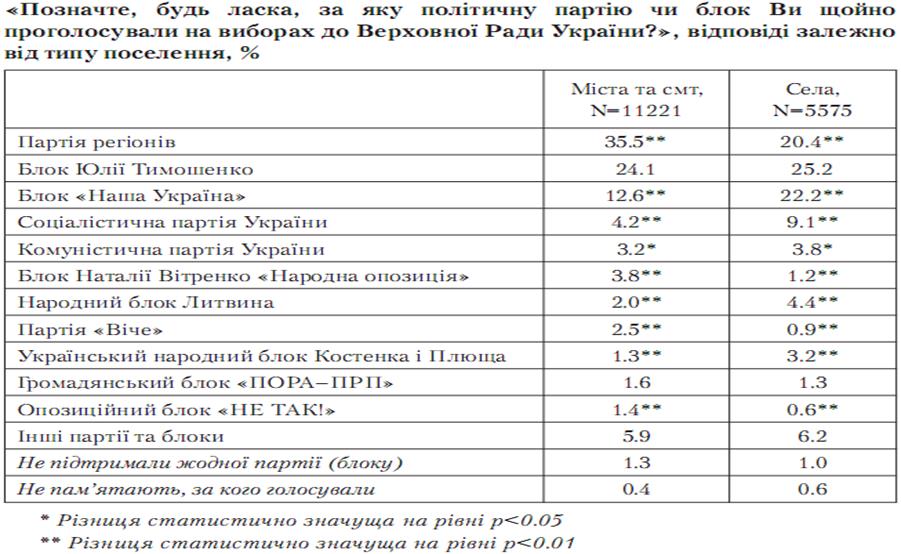
4.Розрахунок значущості розбіжностей відсотків (часток) в пакеті SPSS
Найпростіший спосіб виявлення розходжень часток (відсотків) в пакеті SPSS – застосування критерію хі-квадрат:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.