Измерение емкости конденсаторов с помощью гальванометра
Петрашенко П.Д.
г. Гомель, 2003
Измерение емкости конденсаторов с помощью гальванометра
Цель работы: Изучить метод намерения емкости конденсатора с помощью гальванометра и проверить справедливость формул для последовательно и параллельно соединённых конденсаторов.
Приборы и принадлежности: универсальный источник питания УШ1-2, вольтметр» гальванометр, двухполюсный переключатель, панель с эталонным конденсатором и конденсаторами неизвестной ёмкости и соединительные провода.
Проводником 2-го рода называется вещество, в котором могут перемещаться электрические заряды обоих знаков (растворы и расплавы). Проводником 1-го рода называется вещество, в котором могут перемещаться электрические заряды одного знака (металлы). Если проводник поместить в электрическое поле, то под его влиянием заряды придут в движение и будут накапливаться у поверхности проводника (происходит перераспределение зарядов). Поверхностные заряды создают своё электрическое поле направленное против внешнего. Процесс перераспределения зарядов и усиления компенсирующего электрического поля продолжается до тех пор, пока не исчезнет причина, вызывающая перераспределение зарядов (т.е. результирующее электрическое поле внутри проводника).
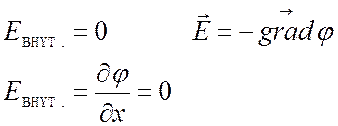
 Напряжённость электрического поля непосредственно у поверхности
проводника направлена по нормали к поверхности, т.к. в противном случае
касательная составляющая поля вызвала бы перераспределение зарядов в
проводнике. Если проводнику сообщить избыточный заряд, то он аналогичным
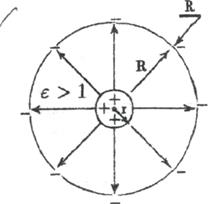
образом распределится по поверхности проводника. Пусть заряженный проводник
имеет форму шара, и создает электрическое
поле подобное полю точечного заряда. При приближении к проводнику других тел,
под действием электрического поля проводника возникают индуцированные (для
проводника) или связанные (для непроводника диэлектрика) заряды. Чтобы внешние тела не влияли на распределение зарядов
по поверхности проводника» его окружают другим проводником или располагают
проводники так, чтобы поле, создаваемое зарядами было сосредоточено только меж
проводниками и не влияло на окружающие тела. Так как напряженность и
потенциал связаны соотношением (по модулю):
Напряжённость электрического поля непосредственно у поверхности
проводника направлена по нормали к поверхности, т.к. в противном случае
касательная составляющая поля вызвала бы перераспределение зарядов в
проводнике. Если проводнику сообщить избыточный заряд, то он аналогичным
образом распределится по поверхности проводника. Пусть заряженный проводник
имеет форму шара, и создает электрическое
поле подобное полю точечного заряда. При приближении к проводнику других тел,
под действием электрического поля проводника возникают индуцированные (для
проводника) или связанные (для непроводника диэлектрика) заряды. Чтобы внешние тела не влияли на распределение зарядов
по поверхности проводника» его окружают другим проводником или располагают
проводники так, чтобы поле, создаваемое зарядами было сосредоточено только меж
проводниками и не влияло на окружающие тела. Так как напряженность и
потенциал связаны соотношением (по модулю):
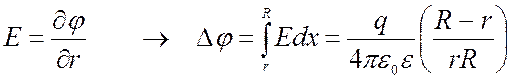
Отношение заряда шара к его потенциалу называют емкостью шара:
Емкость — это свойство проводника, связывающее заряд и потенциал проводника, и зависящее от размеров и формы проводника и от электрических свойств окружающей среды.
Если зазор между сферами d = R-r мал по сравнению с любым радиусом
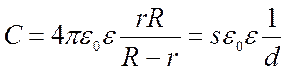
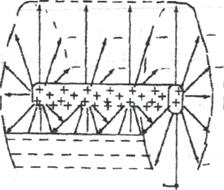
Уединённые проводники обладают малой ёмкостью. Однако электроёмкость проводника возрастает при приближении к нему других тел. Система из двух или более проводников, разделенных диэлектриком, называется конденсатором. Найдем ёмкость плоского конденсатора:
Рассмотрим
случай, когда зазор между обкладками много больше линейных размеров обкладок,
т.е. d<<![]() или d<<
или d<<![]() . Каждая плоская обкладка создаёт поле, подобное полю
бесконечной равномерно заряженной плоскости. Электрическое поле между
обкладками усиливается в 2 раза, а снаружи противоположные поля компенсируются.
Если ось "ох" направить параллельно вектору напряжённости
электрического поля, то в выражении градиента потенциала два слагаемых
обратятся в нули, что существенно упростит математические выкладки. В такой системе координат:
. Каждая плоская обкладка создаёт поле, подобное полю
бесконечной равномерно заряженной плоскости. Электрическое поле между
обкладками усиливается в 2 раза, а снаружи противоположные поля компенсируются.
Если ось "ох" направить параллельно вектору напряжённости
электрического поля, то в выражении градиента потенциала два слагаемых
обратятся в нули, что существенно упростит математические выкладки. В такой системе координат:
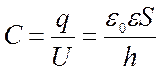
 Два коаксиальных (с общей осью) цилиндра с радиусами "R" и "r" при длинно «L», образуют цилиндрический конденсатор. Если L>>Rто:
электрическое поле такого конденсатора будет подобно полю бесконечной
заряженной нити: Разность потенциалов
между обкладками можно рассчитать по формуле:
Два коаксиальных (с общей осью) цилиндра с радиусами "R" и "r" при длинно «L», образуют цилиндрический конденсатор. Если L>>Rто:
электрическое поле такого конденсатора будет подобно полю бесконечной
заряженной нити: Разность потенциалов
между обкладками можно рассчитать по формуле:
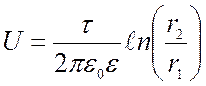
где
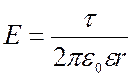 напряженность электрического поля,
созданного цилиндрической заряженной поверхностью,
напряженность электрического поля,
созданного цилиндрической заряженной поверхностью, 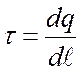 линейная плотность
зарядов. Тогда
линейная плотность
зарядов. Тогда 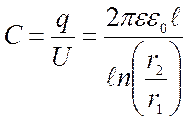
1.
Заданное напряжение равно 16
В. Эталонная емкость равна ![]() . Подключаем по
схеме конденсаторы и снимаем показания с гальванометра все данные заносим в
таблицу:
. Подключаем по
схеме конденсаторы и снимаем показания с гальванометра все данные заносим в
таблицу:
|
1 |
2 |
3 |
4 |
|
|
|
Сxэт. |
13 |
13 |
14 |
14 |
13,5 |
|
Сx1 |
7 |
7 |
8 |
8 |
7,5 |
|
Сx2 |
14 |
15 |
14 |
15 |
14,5 |
|
последовательное |
4 |
5 |
4 |
5 |
4,5 |
|
параллельное |
21 |
22 |
21 |
22 |
21,5 |
2.
Найдем постоянную прибора β,
по формуле 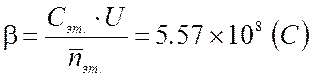
3.
Зная постоянную прибора по
формуле 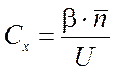 находим неизвестные емкости:
находим неизвестные емкости:
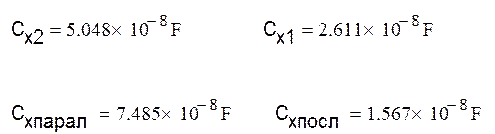
Вывод: Изучили метод намерения емкости конденсатора с помощью гальванометра и проверили справедливость формул для последовательно и параллельно соединённых конденсаторов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.