Компенсация влияния изменения магнитного потока. Ограничение якорного тока. Регулирование уравнительного тока. Двухконтурная САР тока. Демпфирование упругих колебаний за счет системы управления, страница 2

Рисунок 49. Функциональная схема компенсации нелинейностей

преобразователя.

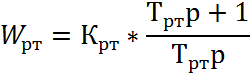
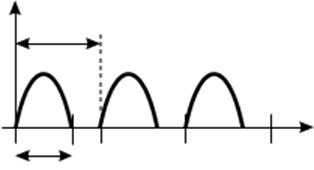
В режиме прерывистого тока ток начинает протекать и спадает до нуля за один интервал проводимости тиристоров, как показано на рис. 50.

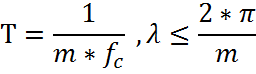
i

                                                      T

t

ωt

Рисунок 50. Диаграмма тока в режиме прерывистого тока.

Среднее значение тока устанавливается в первый же такт коммутации. Т.о., рассматривая  систему  с  непрерывной  частью,  для  которой  полоса пропускания  меньше  частоты  коммутации  тиристоров , электромагнитной инерционностью в силовой цепи можно пренебречь.

Расcматривая  зависимость Ed(I) и Ed(λ) в  соответствии  с  внешними характеристиками  преобразователя  в  режиме  прерывистого  тока, существенное  изменение  ЭДС  можно  представить  как  изменение внутреннего  сопротивления  силовой  цепи  преобразователя Rп при неизменной ЭДС Ed.

С  достаточной  точностью  зависимость  внутреннего  сопротивления  от угла проводимости описывается формулой

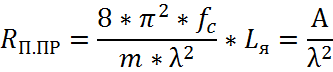
С уменьшением тока интервал проводимости изменяется от  до 0. При этом  Rп  возрастает до бесконечности. Для режима прерывистого тока можно принять, что  . Т.о. объект управления контура тока

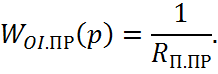
Сдесь на ТО необходим И-регулятор

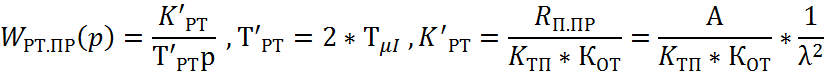
Соответственно  при  переходе  в  режим  прерывистого  тока  регулятор тока должен менять с ПИ на И.

При этом

Подобного  типа регулятор  применяется  в  комплектных  электроприводах  серии  КТЭ.

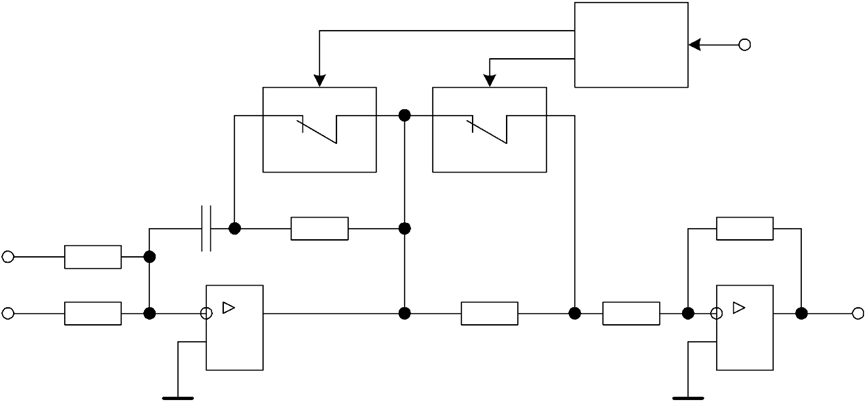
На  схеме  обозначено:  УК1,  УК2 –  управляемые  ключи;  БУК –  блок управления ключами.

В режиме непрерывного тока большой сигнал с датчика тока приводит к размыканию ключей УК1 и УК2. Коэффициент передачи усилителя на DA2

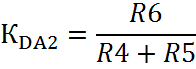
а структура регулятора – ПИ.

                                                                                                                      Uдт

БУК                                          

УК1                    УК2

С1                R3                                                       R6

Uзт    R1

DA1                             R4               R5            DA2         Uy

Uот      R2                

Рисунок 51. Упрощенная принципиальная схема адаптивного регулятора тока.

Если  сигнал  с  датчика  тока  имеет  форму  тока,  то  при  наличии бестоковой паузы БУК замыкает УК1 и переводит УК2 в импульсный режим.

Структура регулятора меняется на И. УК2 управляется широтно-импульсной модуляцией.  Управляющее  напряжение  модулятора  должно  пройти квадратичный  функциональный  преобразователь,  чтобы  скважность  работы

УК2 была пропорциональна .

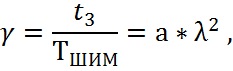
где  – период модуляции,  -  интервал  замкнутого  состояния  УК2.

Тогда,  с  уменьшением   , коэффициент  передачи  регулятора  будет изменяться  от  минимального  до  какого-то  максимального  значения  с зависимостью, обратной .

Настройку  регулятора  можно  упростить,  если  модулирующим сигналом  использовать импульсы от датчика тока, как показано на рис. 52.

При таком построении коэффициент передачи регулятора тока будет обратно пропорционален углу проводимости .

На практике, как правило, датчик тока имеет инерционность (выходной фильтр  узла  гальванической  развязки)  и  его  выходной  сигнал  не соответствует  действительной  форме  тока.  Поэтому  на  вход  БУК  подают сигнал  задания  тока Uзт ,  и  производят  настройку  узла  на  конкретные параметры силовой части данного электропривода.

Подобные  схемы  регулятора  (с  конечным  коэффициентом  передачи регулятора) применяют когда ток холостого хода отличен от нуля

                                 

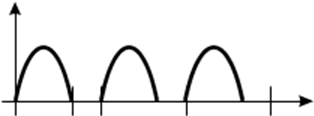
t

Uбук                   УК2 разомкнут

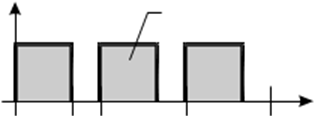
t

Рисунок 52. Диаграмма напряжения БУК.

27. Объект управления с учетом упругой связи

Введем  в  двухмассовую  схему  дополнительно  момент внутреннего трения от  действия  диссипативных  сил,  пропорциональный  разности  скоростей концов упругой связи.

M ВТ  = bВТ  × (w1  - w2 ) .

Теперь  объект  управления  с  учетом  якорной  цепи  двигателя  описывается системой уравнений

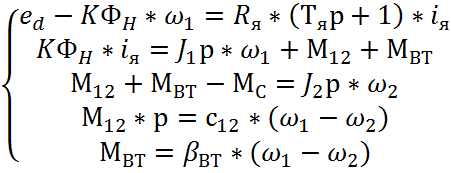
Обозначив  упругий  момент

получим  структурную схему объекта управления, представленную на рис. 53.

Рисунок 53. Структурная схема силовой части электропривода с учетом

упругой механической связи.

Для  упрощения  схемы  и  получения  передаточных  функций  объекта используется обобщенный параметр – период колебаний упругой связи

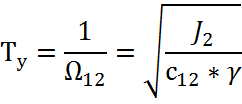
где   - коэффициент жесткости упругой связи,

  -  коэффициент соотношения масс.

Пренебрегая  внешними  силами  (),  после  преобразований  получим структурную схему, показанную на рис. 54.

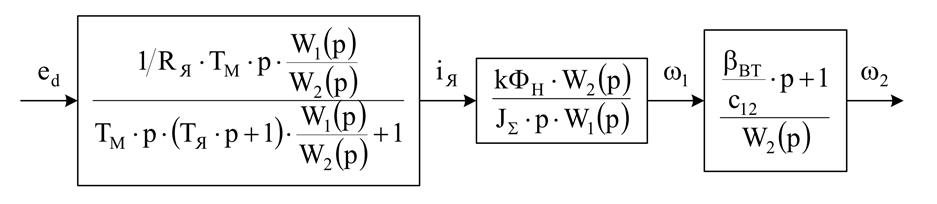
Рисунок 54. Преобразованная структурная схема силовой части

электропривода с учетом упругой механической связи.

На  схеме  и  – полиномы, характеризующие 1-ю и 2-ю массы.

где   - период колебаний второй массы

  -  коэффициент демпфирования упругих колебаний

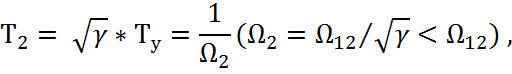
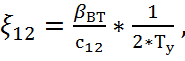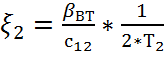  - коэффициент  демпфирования  колебаний  второй массы

Когда частота упругих колебаний соизмерима с полосой пропускания соответствующего контура регулирования, то необходимо проверить влияние упругой связи.

28. Неучет упругой связи при настройке контура тока

Если предположить, что ПИ-регулятор тока настроен как для жесткой системы, то передаточная функция разомкнутого контура

где    -  передаточная  функция  оптимизированного  на технический  оптимум  контура  для  жесткой системы  с  пренебрежением  обратной  связью  по ЭДС,

 - сомножитель,  учитывающий  влияние  обратной связи по ЭДС и упругую механическую связь

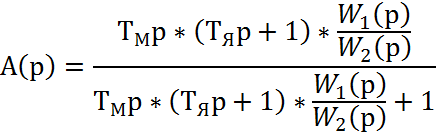
Анализируя  можно  выделить  случаи,  когда  можно  пренебречь упругой связью.

1. Если  приведенный  момент  инерции  второй  массы  значительно  меньше момента  инерции  первой  массы , то коэффициент соотношения масс близок к единице . При этом , и сомножитель  имеет вид такой же как и в жесткой системе.

2. Когда период колебаний имеет значение между  , но параметры системы такие, что упругая связь не вызывает колебаний тока. Поясним при помощи логарифмических характеристик.

Если обозначить

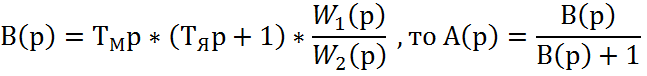
Соответственно для логарифмических характеристик