Министерство образования Республики Беларусь
Гомельский государственный технический университет
имени П. О. Сухого
Кафедра «Автоматизированный электропривод»
ОТЧЁТ
по лабораторной работе №2
«Модели двигателей постоянного тока независимого
и последовательного возбуждения»
Выполнил студент гр. ЭП – 32
Блинков М.В.
Проверил преподаватель
Захаренко В.С.
Гомель 2010
Цель работы: – ознакомиться с алгоритмами моделирования статических
элементов систем автоматического управления;
– ознакомиться с приемами моделирования динамических элементов;
– получить практические навыки составления программ моделирования.
Ход работы
28. Блинков Максим Валерьевич
Двигатель 2ПН90M
(независимое возбуждение). ![]() ,
, ![]() .
.
Моделирование по системе уравнений. Метод Рунге-Кутта.
Справочные данные двигателя:
Напряжение на обмотке якоря
|
|
|
Сопротивление якоря и добавочных полюсов: 15,07 Ом
Индуктивность якоря: 297 мГн
Частота вращения ротора двигателя: 1120 об./ мин.
Число пар полюсов: 1
Инерция якоря: 0,004
КПД: 57 %
При постоянстве магнитного потока ( kФ = kФН = const ) из полной модели двигателя можно исключить цепь возбуждения.
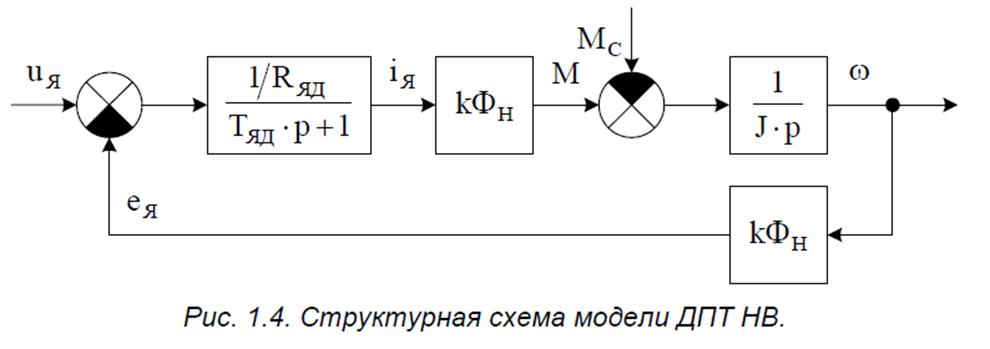
На схеме обозначено:
uЯ – напряжение якоря,
eЯ – ЭДС якоря,
iЯ – ток якоря,
M – момент двигателя,
MС – момент сопротивления,
ω – угловая скорость вращения,
RЯД – активное сопротивление якорной цепи двигателя,
TЯД – постоянная времени якорной цепи
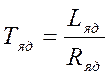
LЯД – индуктивность якорной цепи двигателя.
|
|
|
|
Моделирование по системе уравнений. Метод Рунге-Кутта.
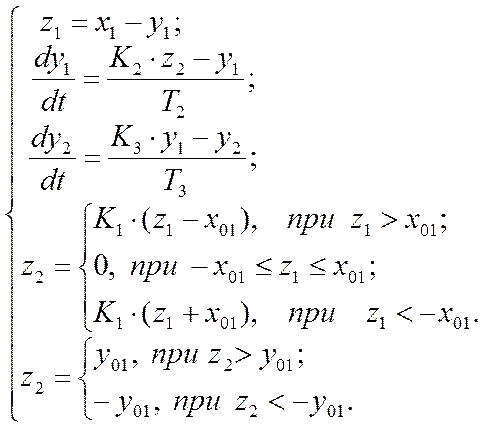
Таблица описания переменных:
|
Переменная |
Описание |
|
u_nom |
Напряжение на обмотке якоря |
|
a |
Число параллельных ветвей якоря |
|
r |
Сопротивление якоря и добавочных полюсов |
|
L |
Индуктивность якоря |
|
n |
Частота вращения ротора двигателя |
|
p |
Число пар полюсов |
|
J |
Инерция якоря |
|
d |
КПД |
|
t,dt |
Шаг расчета |
|
w |
Угловая скорость вращения |
|
I_nom |
Номинальный ток |
|
T_z |
Постоянная времени якорной цепи |
|
M_nom |
Номинальный момент двигателя |
|
k |
Конструктивная постоянная двигателя |
|
kFn |
Произведение конструктивной постоянной на номинальный магнитный поток |
|
t_start, t_full, t_stop, t_revers |
Время пуска, работы, торможения и реверса |
|
i, kol |
Номер шага расчета, количество шагов |
|
f |
Значение производных (правых частей дифф. уравнений) |
|
y, yp, yp1, yp2 |
Значения переменных модели, для которых есть дифференциальные уравнения, на текущем и предыдущем шагах расчета, соответственно |
Кодпрограммы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, Menus, StdCtrls, jpeg, ExtCtrls, Gauges;
type
TForm1 = class(TForm)
Edit_u: TEdit;
Label1: TLabel;
Edit_r: TEdit;
Label_r: TLabel;
Edit_n_ob: TEdit;
Label6: TLabel;
Button2: TButton;
Button3: TButton;
Button4: TButton;
Edit_p: TEdit;
Label8: TLabel;
Label_J: TLabel;
Edit_J: TEdit;
Edit_dt: TEdit;
Label_dt: TLabel;
Label2: TLabel;
Edit_kpd: TEdit;
Button1: TButton;
Label_L: TLabel;
Edit_L: TEdit;
procedure Button4Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
uses Unit2, Unit3, Unit4;
{$R *.dfm}
Type
DArray=array[1..2] of double;
procedure TForm1.Button4Click(Sender: TObject);
begin
close;
end;
procedure TForm1.Button2Click(Sender: TObject);
var
n,p,U_nom,w,I_nom,t_start,t_full,t_stop,t_revers,
r,alpha,L,kFn,T_z,M_nom,J,t,dt,d,k:double;
y,yp,yp1,yp2,f:darray;
i,kol:integer;
function Moment(t,M_nom:double):double;
var
M:double;
begin
if t<=0 then M:=0
else if t<t_start then M:=0.5*M_nom
else if t<t_full then M:=M_nom
else M:=M_nom;
Moment:=M;
end;
function u(t,U_nom:double):double;
begin
u:=0;
if t<=0 then u:=0
else if t<t_start then u:=u_nom
else if t<t_full then u:=u_nom
else if t<t_revers then u:=-u_nom
else if t<t_stop then u:=0;
end;
function sign(x:double):double;
begin
if x>0 then sign:=1
else
if x=0 then sign:=0
else sign:=-1;
end;
procedure scheme(t:double; y:darray; var F:darray);
begin
f[1]:=((u(t,U_nom)-y[2]*kFn)*(1/r)-y[1])/T_z;
f[2]:=(y[1]*kFn-moment(t,M_nom)*sign(y[2]))/J;
end;
procedure method(yp:darray; t,dt:double; var y:darray);
var
x:integer;
f:darray;
f11,f051,f052,y05p:darray;
begin
scheme(t-dt,yp,f);
for x:=1 to 2 do
y05p[x]:=yp[x]+(dt/2)*f[x];
scheme(t-0.5*dt,y05p,f051);
for x:=1 to 2 do
y05p[x]:=yp[x]+(dt/2)*f051[x];
scheme(t-0.5*dt,y05p,f052);
for x:=1 to 2 do
y[x]:=yp[x]+dt*f052[x];
scheme(t,y,f11);
for x:=1 to 2 do
y[x]:=yp[x]+(dt/6)*(f[x]+2*f051[x]+2*f052[x]+f11[x]);
end;
begin
n:=strtofloat(Edit_n_ob.Text);
U_nom:=strtofloat(Edit_u.Text);
r:=strtofloat(Edit_r.Text);
L:=strtofloat(Edit_L.Text);
p:=strtofloat(Edit_p.Text);
d:=strtofloat(Edit_kpd.Text);
J:=strtofloat(Edit_J.Text);
dt:=strtofloat(Edit_dt.Text);
L:=L*exp((-3)*ln(10));
d:=d/100;
r:=r*(1+0.0039*(120-15));
I_nom:=U_nom*(1-d)/(2*r);
w:=3.14*n/30;
kFn:=(U_nom-r*I_nom)/w;
T_z:=L/r;
M_nom:=kFn*I_nom;
k:=1/r;
t_start:=0.3;
t_full:=t_start+0.3;
t_revers:=t_full+0.3;
t_stop:=t_revers+0.1;
kol:=round(t_stop/dt);
fillchar(y,sizeof(y),0);
fillchar(yp,sizeof(yp),0);
Form2.Series1.Clear;
Form2.Series2.Clear;
Form3.Series1.Clear;
t:=0;
Form2.Series1.AddXY(t,y[1]*10);
Form2.Series2.AddXY(t,y[2]);
Form3.Series1.AddXY(y[1],y[2]);
for i:=1 to kol do
begin
t:=dt*i;
method(yp,t,dt,y);
Form2.Series1.AddXY(t,y[1]*10);
Form2.Series2.AddXY(t,y[2]);
Form3.Series1.AddXY(y[1],y[2]);
yp2:=yp1;
yp1:=yp;
yp:=y;
end;
Button3.visible:=true;
Button1.Visible:=true;
end;
procedure TForm1.Button3Click(Sender: TObject);
begin
Form2.showmodal;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Form3.showmodal;
end;
end.
График переходных процессов
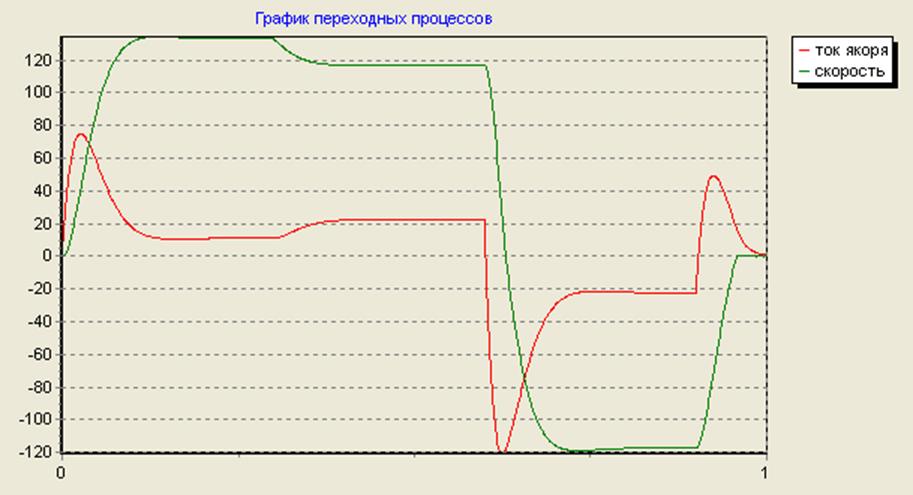
График динамической характеристики
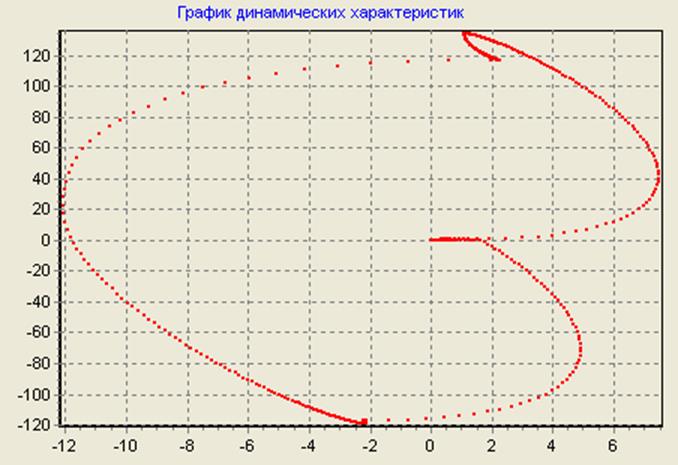
Выводы:
В результате выполнения данной лабораторной работы закрепил полученные практические навыки составления программ моделирования; а также исследовал динамические свойства двигателя постоянного тока Д31 последовательного возбуждения с учетом кривой намагничивания, при этом построил в одних осях диаграммы тока и скорости, и динамическую механическую характеристику.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.