Методы принятия решений, самостоятельная работа, страница 4

Таким образом, мы определили показатели надёжности для всех элементов нашей системы, а так же для условных объединений этих элементов в блоки.

Далее приступаем к расчету показателей надёжности всей системы.

Формулы расчёта показателей надёжности системы соответствуют экспоненциальному закону надёжности.

Найдём интенсивность отказов всей системы:

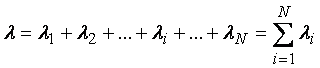
Определим вероятность безотказной работы в течении заданного времени t.

Cогласно стандарту, для систем измерения и управления технологическими процессами время t следует выбирать из следующего ряда значений (в часах): 250, 500, 1 000, 2 000, 4 000, 8 000, 16 000.

Назначим срок эксплуатации – время t,  исходя из характерного для системы интервала времени - рабочего квартала, равное 2000 ч.

Вероятность безотказной работы в течении t=2000ч  составляет:

Вероятность безотказной работы  округляется до ближайшего из указанного ниже ряда значений: более 0,999; 0,999; 0,998; 0,997; 0,996; 0,995; 0,994; 0,993; 0,992; 0,99; 0,98; 0,97; 0,96; 0,95; 0,94; 0,93; 0,92; 0,9; 0,88; 0,87; 0,85; 0,82; 0,8. Вероятность  не должна получаться меньше 0,8. В противном случае нужно взять меньшее значение t.

В нашем случае она получилась больше значения 0,8, значит время t выбрано правильно.

После округления имеем:

Определим среднее время безотказной работы каждого блока (среднюю наработку до отказа).

В случае экспоненциального закона надежности между и существует простая связь:

В этом случае получим:

T₀₁ = 1/λ₁ = 84 000 ч, T₀₂ = 1/λ₂ = 43 000 ч, T₀₃ = 1/λ₃ = 645 000 ч,

Далее определимся со средним значениями среднего времени восстановления каждого блока системы.

Согласно стандарту, среднее время восстановления следует  выбирать  из  ряда: 1, 5, 10, 20, 40, 60 мин  и  2, 4, 6, 8, 12, 18, 24, 36, 48 ч

Примем следующие значения среднего времени восстановления каждого блока:

Т_В1 = 8 ч, Т_В2 =  12 ч, Т_В3 = 4 ч

Определим коэффициент готовности системы по формуле:

,

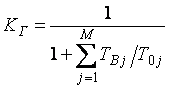где – среднее время безотказной работы; – среднее время восстановления 

j– го блока; M – число блоков

 

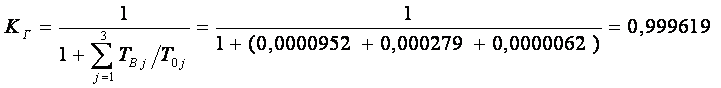
Округляем полученное значение:

                           0,999 6       

Итак, окончательный ответ на поставленную задачу:

-  вероятность безотказной работы системы в течение 2 000 ч равна 0,93;

-  коэффициент готовности равен 0,999 6.