





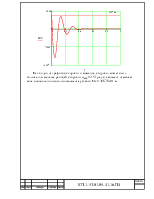
8. Анализ переходных процессов.
Расчет и анализ переходных процессов за цикл работы механизма позволяет определить продолжительность процессов, закон изменения скорости, путь, проходимый рабочим органом, а также позволяет провести уточненную проверку двигателя по нагреву и перегрузочной способности.
Исходная система уравнений:
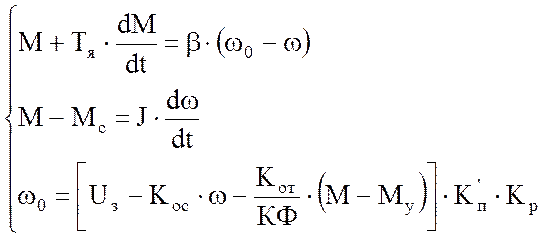
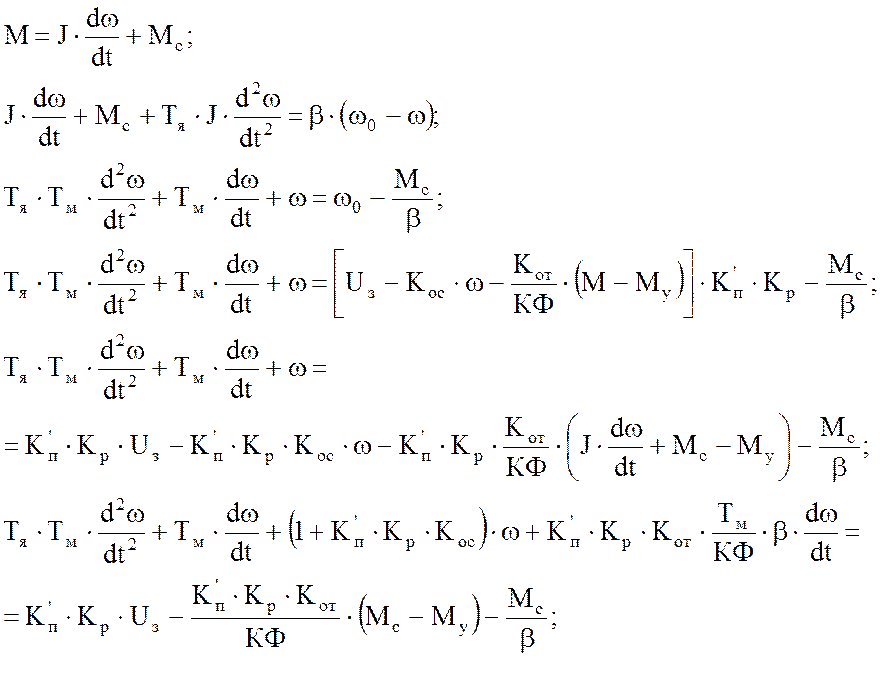
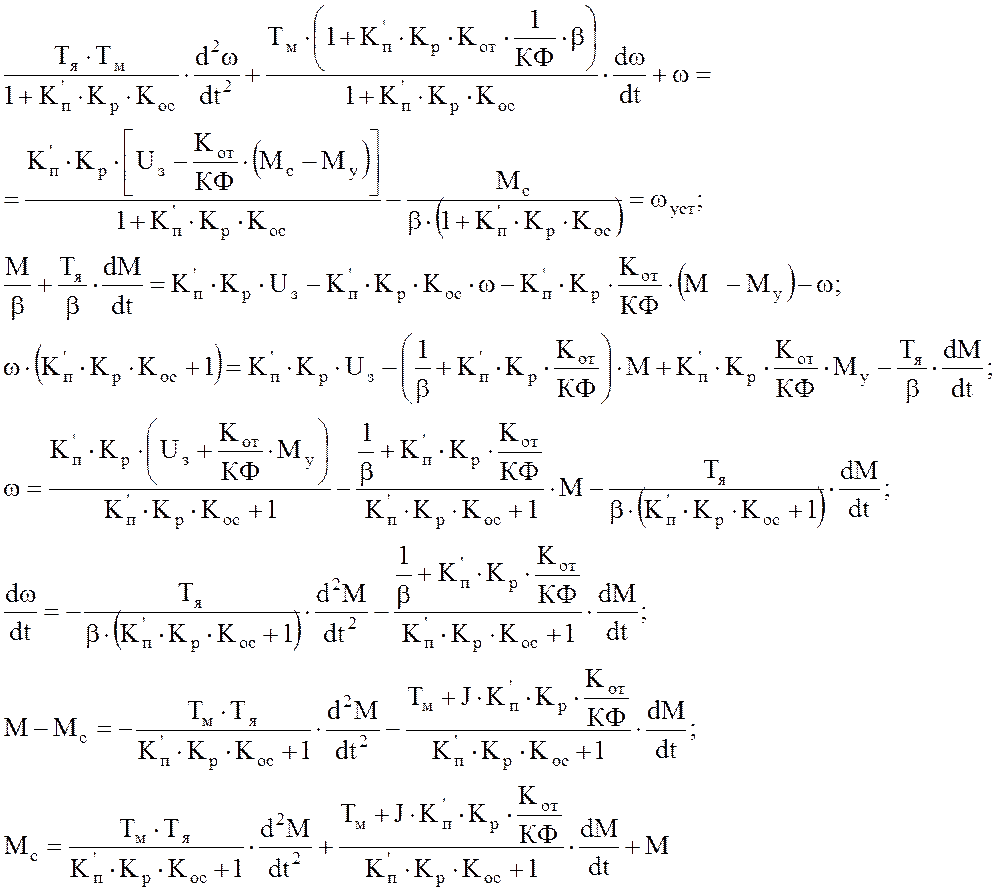
Рассчитаем аналитически переходные процессы M(t) и ω(t).
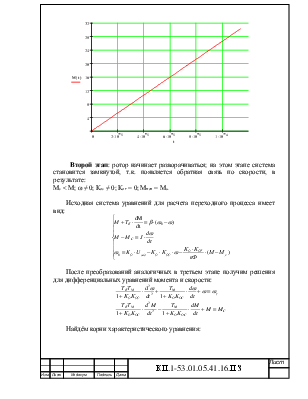
Первый этап: время, до которого якорь находится в неподвижном состоянии, т.е. М ≤ Мс; ω = 0; Кос = 0; Кот = 0.
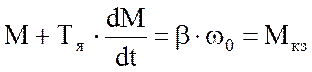
Решение данного уравнения:
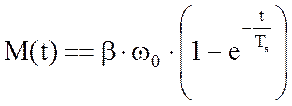
Первый этап завершиться в момент времени:
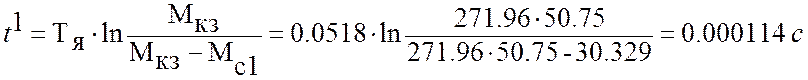
Подставляя в
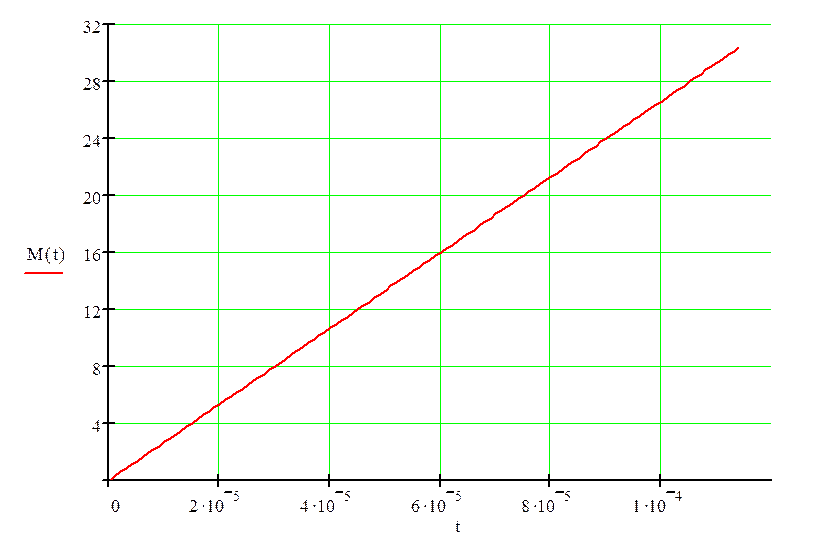
решение уравнения значение времени t от 0 до ![]() ,
построим кривую M(t) до значения Мс1 = 30.329 Н·м (рис.10).
,
построим кривую M(t) до значения Мс1 = 30.329 Н·м (рис.10).
Второй этап: ротор начинает разворачиваться; на этом этапе система становится замкнутой, т.к. появляется обратная связь по скорости, в результате:
Мс < М; ω ≠ 0; Кос ≠ 0; Кот = 0; Мнач = Мс.
Исходная система уравнений для расчета переходного процесса имеет вид:
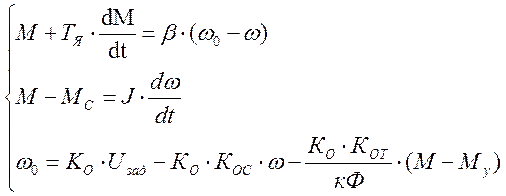
После преобразований аналогичных в третьем этапе получим решения для дифференциальных уравнений момента и скорости:
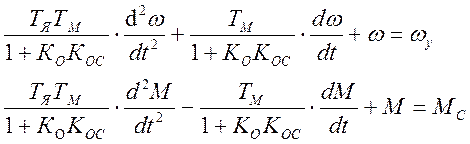
Найдём корни характеристического уравнения:
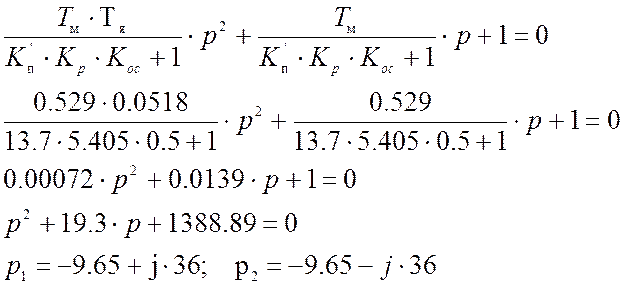
Решения данного уравнения:
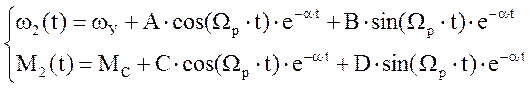
α = 9.65; Ωр
= 36; ωm = 12.15 рад/с![]()
![]()
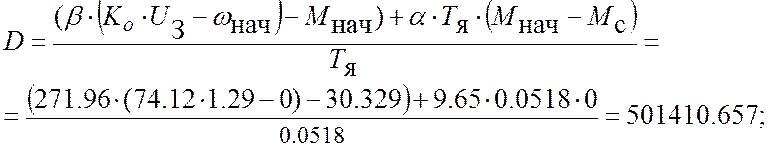
С = Мнач – Мс = 0
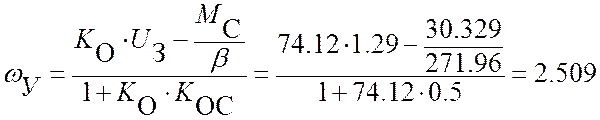
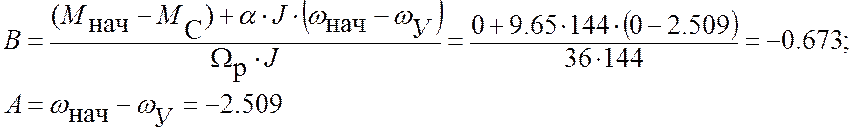
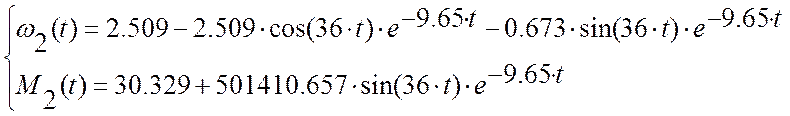
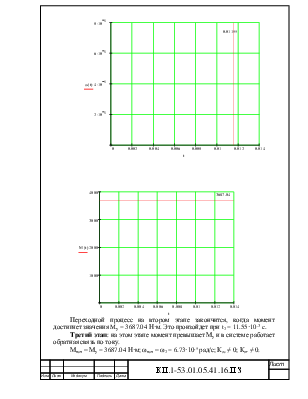
Подставляя в решения уравнений значения времени, построим кривые ω(t) и М(t) (рис. 7).
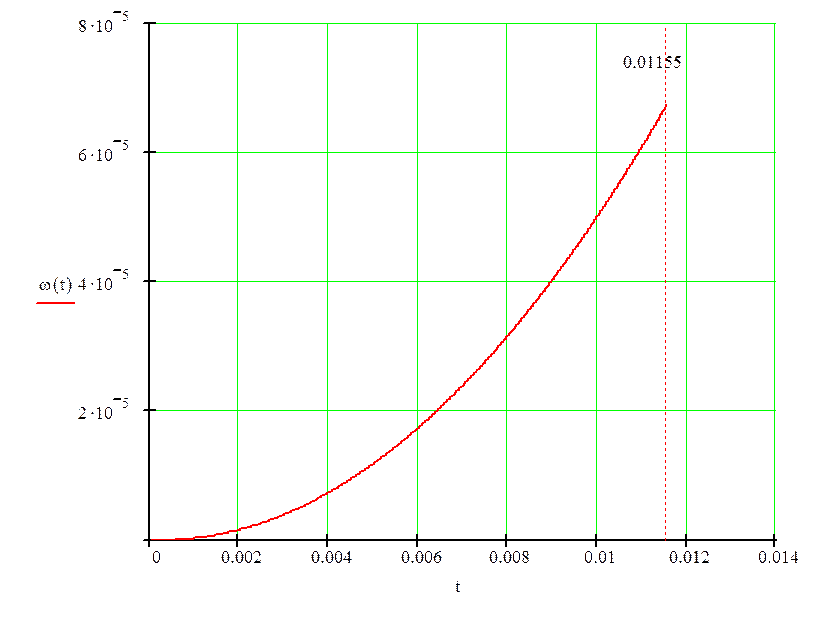
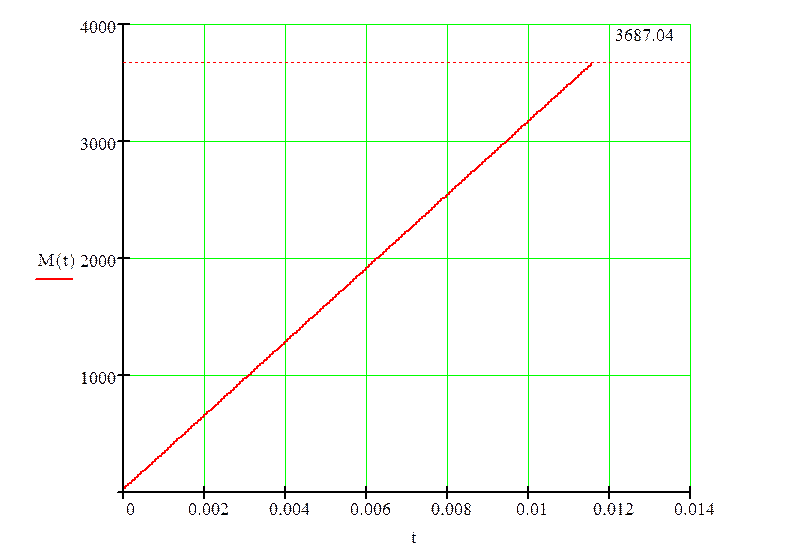
Переходной процесс на втором этапе закончится, когда момент достигнет значения Mу = 3687.04 Н·м. Это произойдет при t2 = 11.55·10-3 c.
Третий этап: на этом этапе момент превышает Му и в системе работает обратная связь по току.
Мнач = Му = 3687.04 Н·м; ωнач = ω2 = 6.73·10-5 рад/с; Кос ≠ 0; Кот ≠ 0.
Исходная система уравнений для расчета переходного процесса имеет вид:
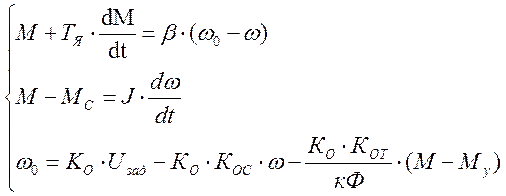
Преобразуем исходную систему уравнений, подставив 3-е уравнение в 1-ое.
(*) 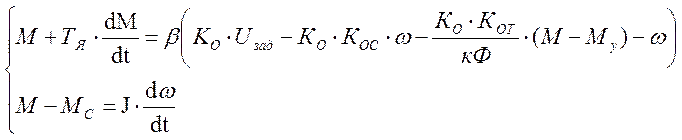
Получим из 2-го уравнения выражение для момента 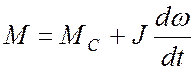 и подставим его в первое уравнение.
и подставим его в первое уравнение.
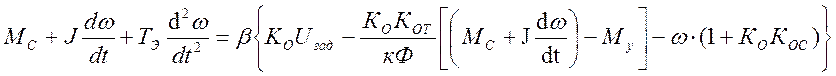
Умножим обе части уравнения на 1/β и раскроем скобки. Разделив переменные, получаем:
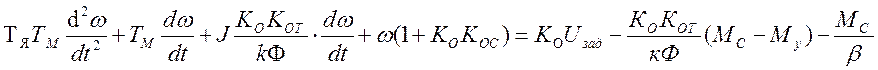
Разделим обе части уравнения на (1+КОКОС):
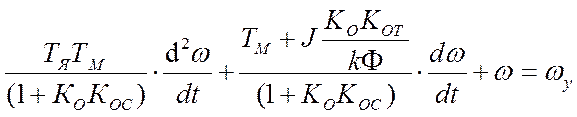
![]()
Решения для дифференциальных уравнений момента и скорости:
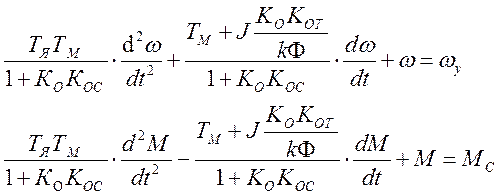
ищутся в виде частного решения или вынужденной составляющей, которая определяется правой частью общего решения однородного дифференциального уравнения, которое описывает свойства и представляет собой левую часть. Поведение свободных составляющих определяется корнями характеристического уравнения:
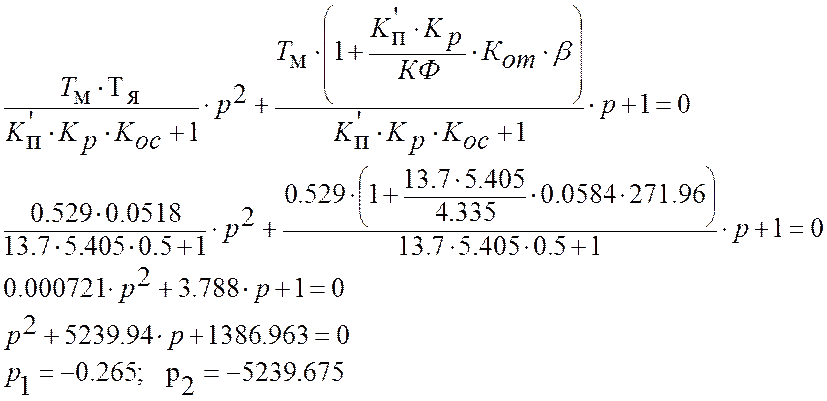
Решения данного уравнения:
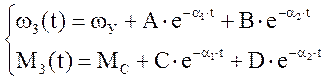
α1 = 0.265; α2 = 5239.675; ωm = 12.15 рад/с.
![]()
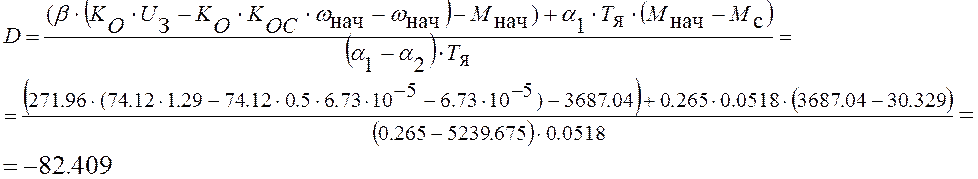 С
= Мнач – Мс – D = 3687.04 – 30.329 + 82.409 = 3739.12
С
= Мнач – Мс – D = 3687.04 – 30.329 + 82.409 = 3739.12
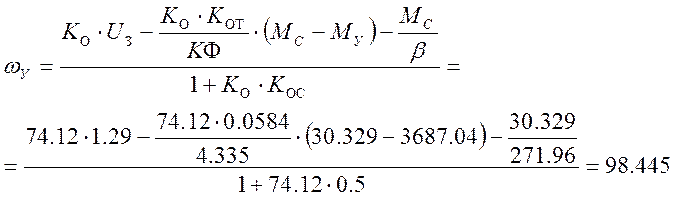
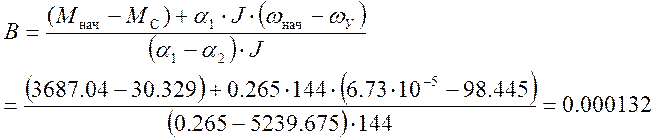
А = ωнач – ωу = 6.73·10-5 – 98.445 = –98.445
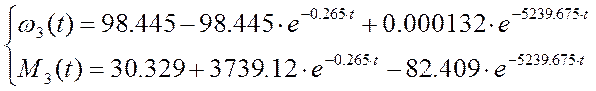
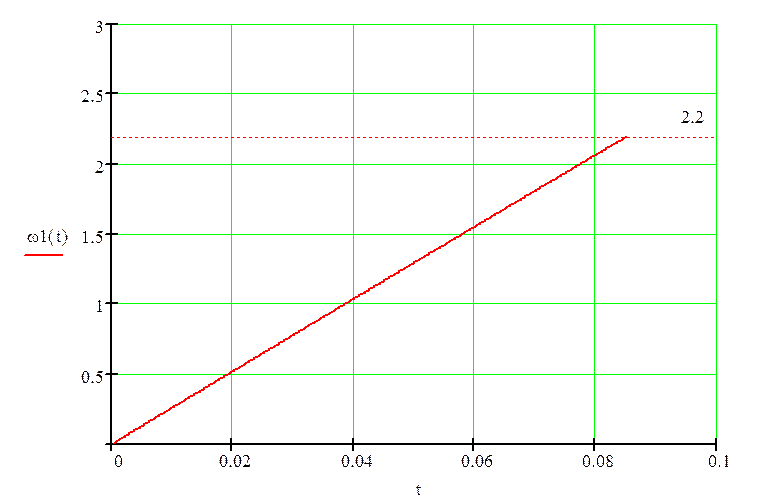
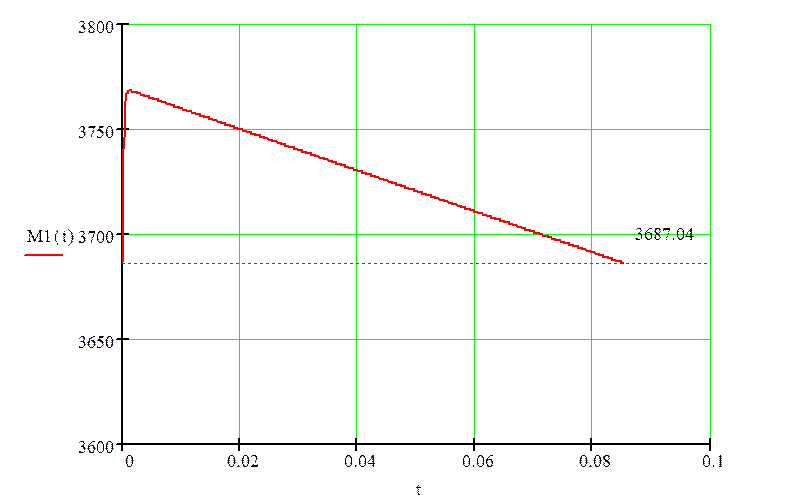
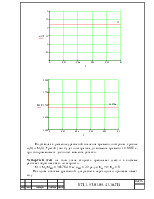
Подставляя в решение уравнений значения времени, построим кривые ω3(t) и М3(t). Третий этап будет повторяться до момента времени t = 0.085 с, при котором момент достигнет момента уставки.
Четвертый этап: на этом этапе скорость превышает ωраб и в системе работает обратная связь по скорости.
М < Му; Мнач = 3687.04 Н·м; ωнач = 2.2 рад/с; Кос ≠ 0; Кот = 0.
Исходная система уравнений для расчета переходного процесса имеет вид:
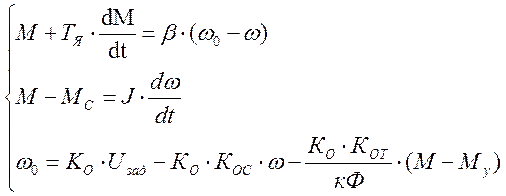
После преобразований аналогичных в третьем этапе получим решения для дифференциальных уравнений момента и скорости:
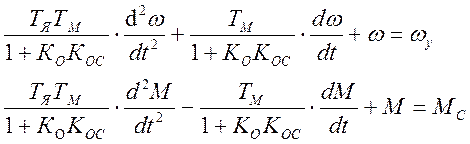
Найдём корни характеристического уравнения:
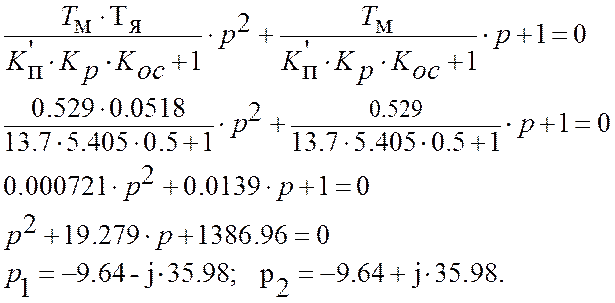
Решения данного уравнения:
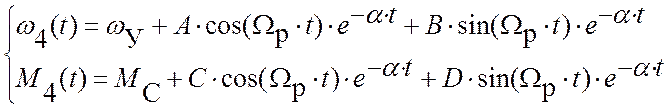
α = 9.64; Ωр = 35.98; ωm = 2.2 рад/с
![]()
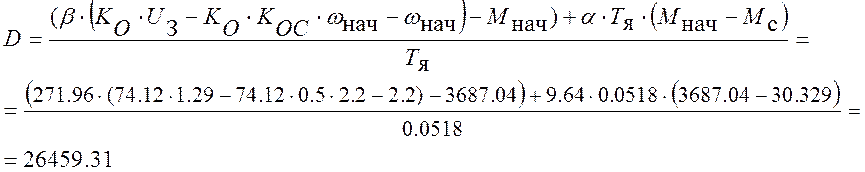
С = Мнач – Мс = 3687.04 – 30.329 = 3656.711
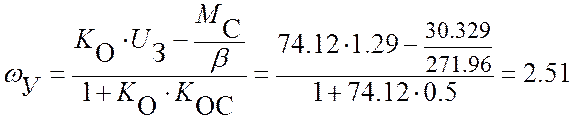
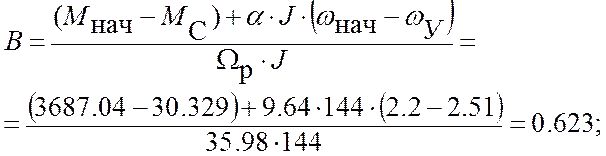
А = ωнач – ωу = 2.2 – 2.51 = ─ 0.51;
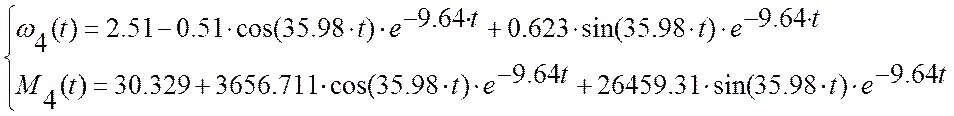
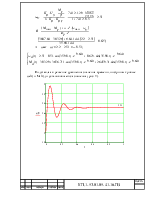
Подставляя в решение уравнения значения времени, построим кривые ω4(t) и М4(t) до установившегося значения (рис. 9).
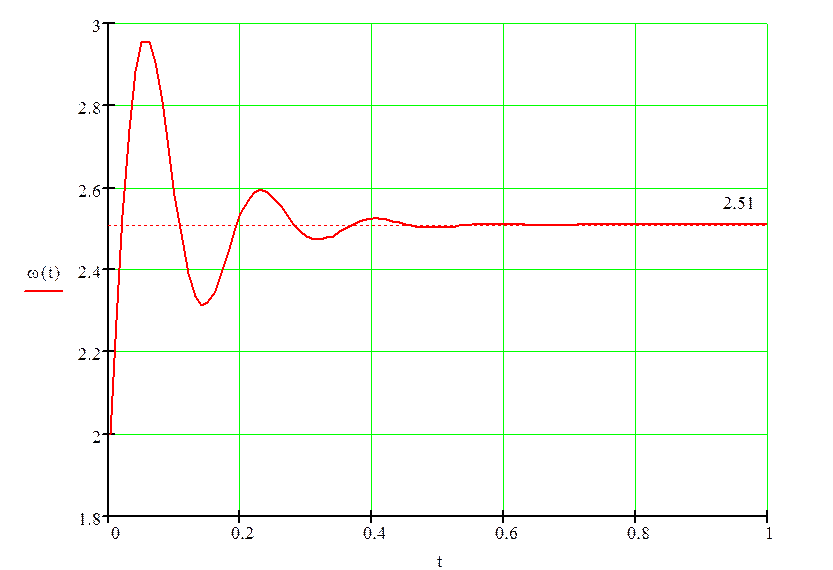
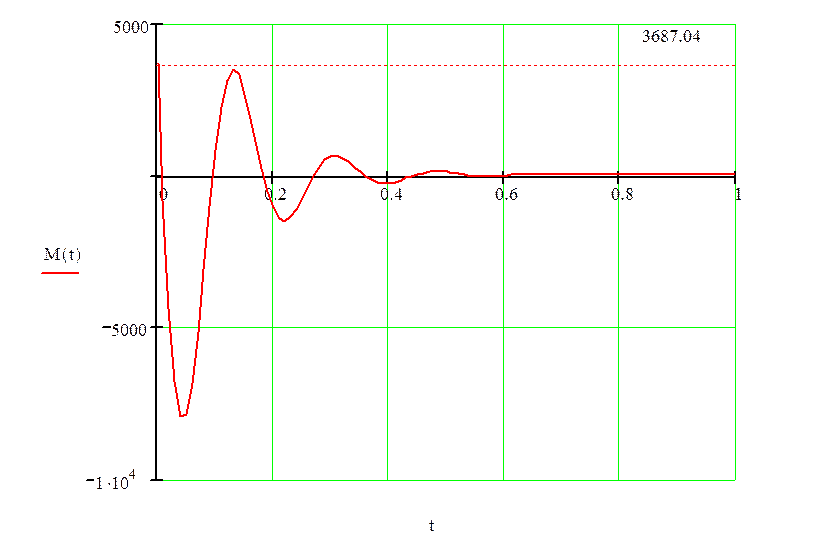
Как видно из графиков скорости и момента, скорость может быть больше или меньше рабочей скорости ωраб = 2.51 рад/с, а момент изменяет свое значение относительно момента уставки Му = 3687.04 Н·м.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.