 РГР 1
РГР 1
№ 715
Nk = 2
E1 = 100 В
E2 = 300 В
R1 = 30 Ом
R2 = 40 Ом
R3 = 20 Ом
R4 = 18 Ом
R5 = 26 Ом
R6 = 50 Ом
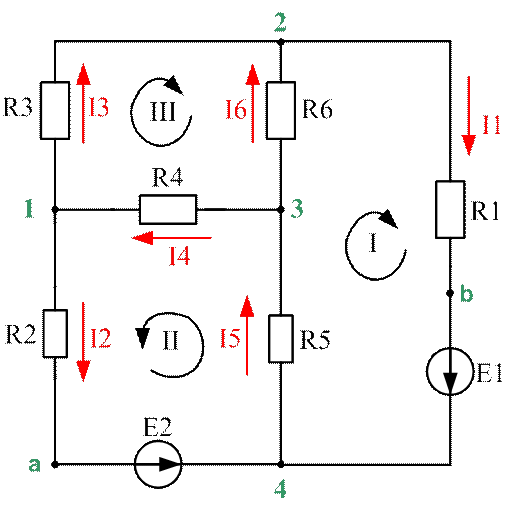
Рис.1
1. Система уравнений Кирхгофа
По 1-му закону Кирхгофа (для узлов 1,2,4)
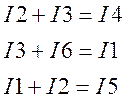
По 2-му закону Кирхгофа (для контуров I,II,III)
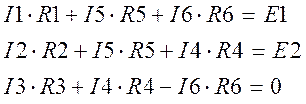
2. Метод контурных токов
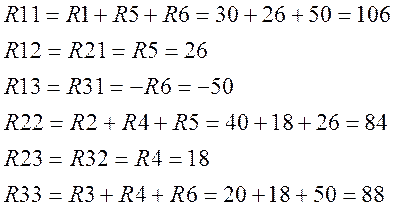
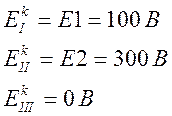
Получаем следующую систему линейных уравнений в матричной форме:
106 26 -50 I1k 100
26 84 18 I2k = 300
-50 18 88 I3k 0
Для решения системы применяем метод Крамера:
Находим главный определитель матрицы R:
106 26 -50
D = 26 84 18 = 106*(84*88 - 18*18) - 26*(26*88 + 18*50) - 50*(26*18 + 84*50) = 432920
-50 18 88
Находим определитель 1-го алгебраического дополнения:
100 26 -50
D11 = 300 84 18 = 100*(84*88 - 18*18) - 26*(300*88 - 0*18) - 50*(300*18 - 0*84) = -249600
0 18 88
Находим определитель 2-го алгебраического дополнения:
106 100 -50
D22 = 26 300 18 = 106*(300*88 - 0*18) - 100*(26*88 + 18*50) - 50*(26*0 + 300*50) = 1729600
-50 0 88
Находим определитель 3-го алгебраического дополнения:
106 26 100
D33 = 26 84 300 = 106*(84*0 - 300*18) - 26*(26*0 + 300*50) + 100*(26*18 + 84*50) = -495600
-50 18 0
Находим контурные токи
I1 = I1k = D11/D = - 249600/432920 = -0.577 А
I2 = I2k = D22/D = 1729600/432920 = 3.995 А
I3 = I3k = D33/D = - 495600/432920 = -1.145 А
Теперь, по 1-му закону Кирхгофа определим остальные токи:
I4 = I2 + I3 = 3.995 - 1.145 = 2.85 А
I5 = I1 + I2 = -0.577 + 3.995 = 3.418 А
I6 = I1 – I3 = -0.577 + 1.145 = 0.568 А
3. Упрощение схемы ( «Треугольник» в «Звезду» ) и расчет токов методом узлового напряжения
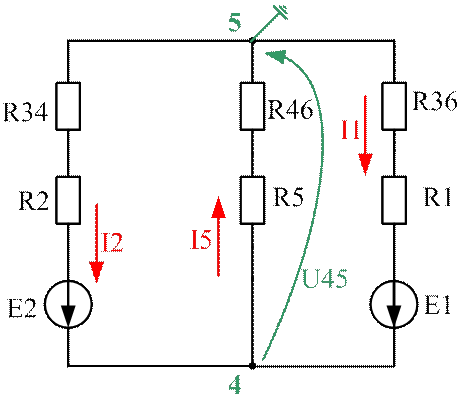 |
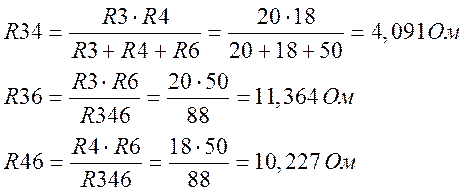
Рис.2
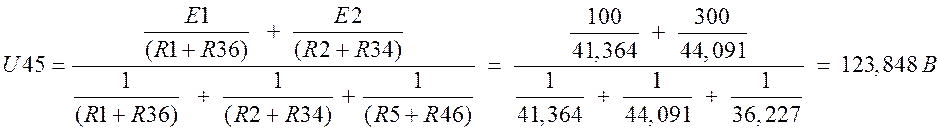
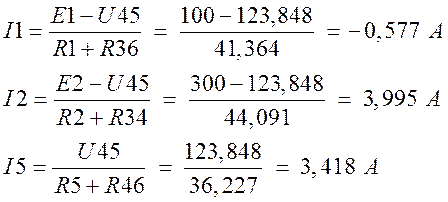
Вернемся к рис.1 и найдем остальные токи, выразив их из уравнений по 2-му закону Кирхгофа:
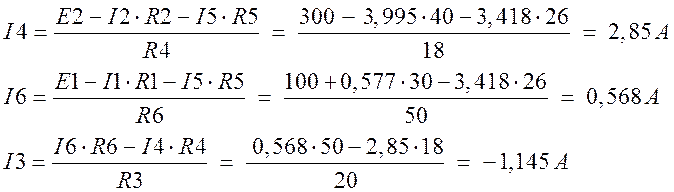
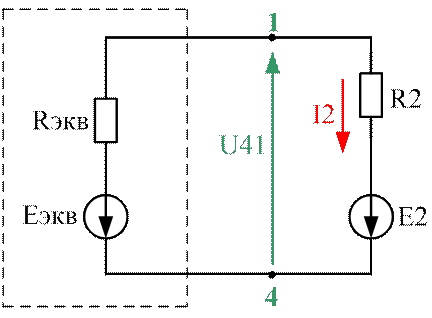
4. Ток (I2) методом эквивалентного генератора
a) Находим Rэкв
 |
![]()
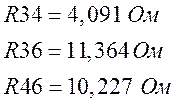
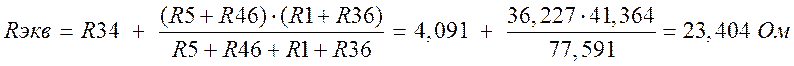
б) Находим Eэкв )
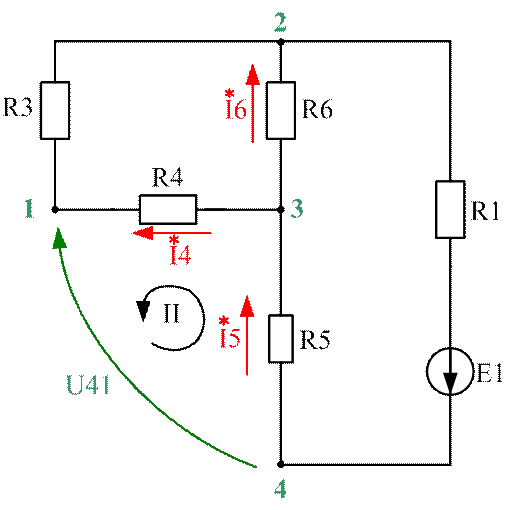
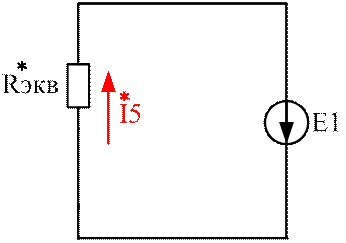 |
|||
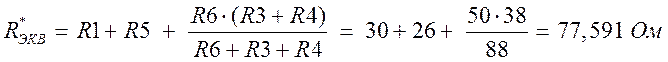
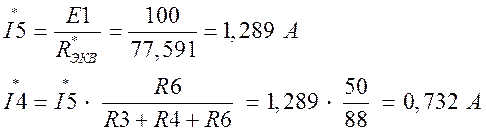
Составим по 2-му закону Кирхгофа ур-е для контура 2 и выразим из него U41 = Eэкв :
![]()
 |
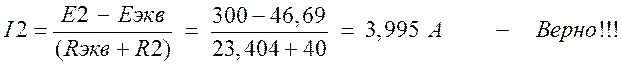 |
5. Баланс мощностей
![]()
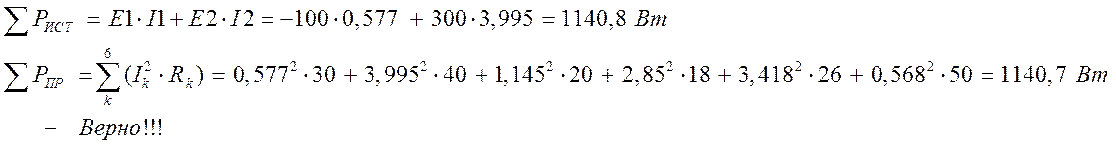
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.