Розробка плану вибіркового контролю якості виробів РЕА та МЕА по кількісним характеристикам, страница 2

Кривые, характеризующие вероятность риска изготовителя и приемщика, связанную с использованием определенного плана контроля, называют оперативными характеристиками (ОХ) выборочного контроля. На оси абсцисс отмечается качество предъявляемой ОТК продукции, а на оси ординат – вероятность ее принятия.

Оперативная характеристика выборочного контроля наглядно показывает зависимость между величинами α, β, q₁, q₂и параметрами плана (объемом выборки и приемочным критерием). Кривая дает информацию о жесткости контроля и об эффективности выбранного плана, служит для оценки и сравнения различных методов выборочного контроля. На кривых оперативных характеристик выделяют несколько точек, которые определяют построение и расчет плана выборочного контроля. Такими характерными точками являются:

1. Приемочный уровень качества – это точка кривой ОХ, имеющая координаты q₁ и 1- α. На практике показатель приемлемого уровня качества выбирается так, чтобы обеспечивалась 95% - ая вероятность принятия продукции приемлемого качества q₁  при возможном 5 %-ом риске изготовителя. Это значит, что при выборочной проверке партий приемлемого качества в среднем 95% из них будет принято.

Вследствие ошибок 1-го и 2-го рода возможно забракование годных и принятие партий худшего качества.

Этот недостаток выборочных методов неустраним, и степень риска характеризуется крутизной кривой ОХ, которая, в свою очередь, зависит от объема выборки, от доли дефектных изделий в партии, от уровня принятия или бракования.

Выборочный план тем лучше, чем ближе его оперативная характеристика к идеальной, которая может быть получена при 100%-ном контроле, и чем меньше области ошибочного бракования и приемки партий. С увеличением крутизны ОХ возрастает объем выборки, а следовательно, и стоимость контроля. Так возникает задача расчета оптимального плана контроля.

2.  Допустимый предел дефектных изделий в одной партии является второй характерной точкой оперативной характеристики, которая имеет координаты q₂и  β. Обычно устанавливается риск приемщика β = 0,1; это означает, что с 10%-ой вероятностью контролер может принять партии изделий, качество которых ниже приемлемого уровня  q₂.

3.  Точка равного риска для изготовителя и приемщика – это такой уровень качества, при котором партия изделий имеет одинаковую вероятность принятия и забракования, т.е. Р = Q = 0,5.

4.  Крайние точки оперативной характеристики соответствуют предельным значениям качества продукции. Крайняя верхняя точка ОХ соответствует тем случаям, когда в предъявляемых на контроль проверяемых партиях нет брака (q = 0), и, следовательно, вероятность их принятия Р = 1,0. Крайняя нижняя точка ОХ отражает невозможность принятия (Р = 0) партий содержащих все дефектные изделия (q = 1).

Кривая оперативной характеристики для конкретного случая строится по значениям Р и q с использованием следующих формул[2]:

                                                            (3.3)

где Т определяется по формуле (3.1);

       n – объем выборки, вычисляемый по формуле (3.2).

Вычисленное значение h используется для определения K_q, по формуле[2]:

K_q = Т – h∙U_p ,                                                                (3.4)

где U_p – квантили нормального распределения для выбранных значений вероятности Р приемки партии.

По полученным расчетным данным строят оперативную характеристику как функцию Р = f(q), а по данным выборки оценивают среднее значение  и среднее квадратическое отклонение s(y) контролируемого параметра. После построения оперативной характеристики можно оценить максимальное среднеквадратическое отклонение[2]:

                                                    (3.5)

где - нормальные отклонения с вероятностями, соответственно q_н и  q_в их превышения;

q_н и  q_в – оценки доли дефектных изделий за нижней и верхней границами допуска.

Критерии приемки или забракования при известных  и s(y) служат выражения[2]:

для верхней y_в  заданной границы

+ Т ∙ s(y)≤  y_в;               (3.6)

для нижней  y_н  заданной границы

- Т ∙ s(y) ≥ y_н;                                                             (3.7)

для двусторонних границ – соотношения (3.6) и (3.7), а также

s(y ) ≤ σ_max.  .                                                                (3.8)

При известном среднем значении  и среднеквадратическом отклонении s(y) объем выборки существенно уменьшается и вычисляется более просто по формуле[2]:

                                                   (3.9)

Это новое значение   вводится в формулу[2] для вычисления величины  т.е:

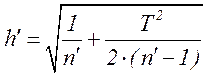 .                                                    (3.10)

При существенном отличии законов распределения контролируемых параметров от нормального закона в расчет плана приемочного контроля вводят коррективы. Характер и степень отклонения реального распределения от кривой Гаусса оценивают по коэффициентам относительной асимметрии α_i и относительного рассеивания k_i. Критерии приемки в этом случае принимают новый вид[2]:

для верхней границы допуска

N(y)+ L_в ∙ σ(y ) ≤  y_в ,(3.11)

где  

      L_в = Т  * (k_i + α_i);                                                         (3.12)

для нижней границы допуска

N(y) – L_н ∙ σ(y) ≥ y_н ,(3.13)

где

L_н = Т ∙ (k_i - α_i).                                                                       (3.14)