Расчёт вероятности безотказной работы системы по экономическим показателям, расчёт методом “Сверху вниз” вероятности безотказной работы блоков системы, расчёт вероятности безотказной работы двух структур известными методами, страница 2

Получаем:

Так как элементы равнонадёжные, то

.

Вероятность безотказной работы всей системы:

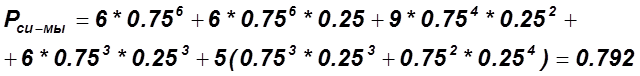
Расчёт структуры №8 (рис.2):

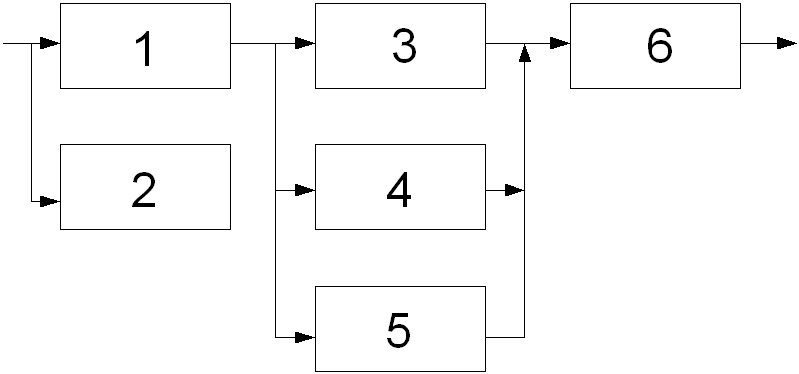
Структура №8 является простейшей. Более приемлемый расчёт такой структуры является классический метод.

         Блоки 1 и 2 соединены параллельно, следовательно, их общая вероятность безотказной работы будет равна:

Блоки 3, 4 и 5 также соединены параллельно. Их общая вероятность безотказной работы будет равна:

         Так как элементы равнонадёжные (), то общая вероятность структуры равна:

         Найдём вероятность первых двух блоков:

Найдём вероятность блоков 3, 4 и 5:

         Вероятность блока 6 равна:

         Общая вероятность структуры равна:

4. Расчет параметров СМО.

4.1 Среднее число заявок в системе :

,  

         4.2 Определяем вероятность состояния системы P_k:

               

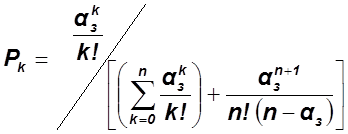
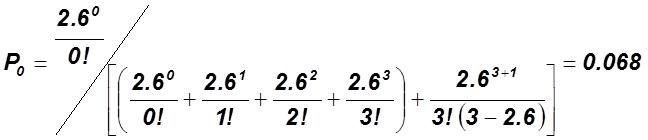
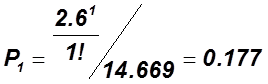
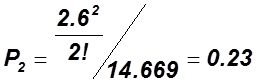
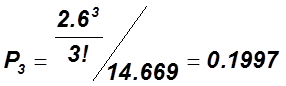
4.3 Определяем вероятность наличия очереди Р_оч:

         4.4 Определяем среднюю длину очереди m_оч:

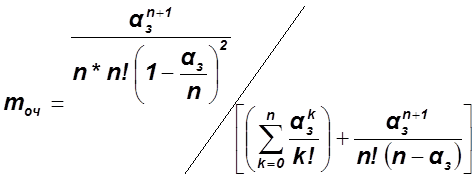
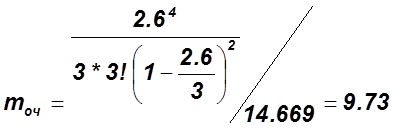
         4.5 Определяем среднее время пребывания заявки в очереди t_оч:

t_оч=m_оч/

t_оч=9.73/4=2.43c.

5. Расчёт объёма представительной выборки для испытания на надёжность.

         - вероятность для изготовителя;

         - характеризует риск изготовителя;

     - вероятность для заказчика;

- характеризует риск заказчика;

     С=1 – приёмочное число отказов в представительной выборке;

5.1 для неизвестного закона распределения:

·  С учётом заказчика:

     Задана вероятность безотказной работы  и , характеризующий риск заказчика.

Необходимо найти объём представительной выборки n:

1.)  определяем С=0;

2.)  по таблице П2 в зависимости от браковочной вероятности безотказной работы , приёмочного числа С=1  и риска заказчика  (закон распределения Пуассона) находим:

  n=11 шт.

·  С учётом заказчика и изготовителя:

     Задана  вероятность для изготовителя, его риск ( и ) и  вероятность для заказчика и его риск ( и ). Задача решается с помощью коэффициента А:

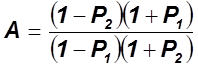
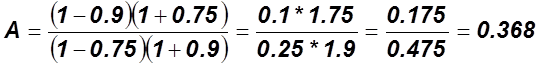
А=0.368. Принимаем А=1.

         По таблице П3 определяем значение вспомогательного коэффициента А в зависимости от риска изготовителя, заказчика и приёмочного числа С:

         при С=0 А=4.4

     при С=1 А=2.6

     при С=2  А=2.1

Принимаем С=2.

По таблице для заданных С=2, , Р=0.8, определяем n=17шт.

5.2 для известного закона распределения:

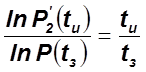     - для экспоненциального закона;

Р=0.75, t_з=500,

1.)  задаёмся временем испытаний: t_и=250;

2.)  определяем соотношение:  ;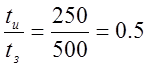

3.)  задаёмся С=2;

4.)  по таблице П2 для заданных С=2, , Р₂’=0.8944(0.5):

n=33шт.

5.3 графическим методом

         Графический метод планирования испытаний основан на использовании семейства кривых распределения Пуассона, характеризующих зависимость вероятности числа d отказавших изделий, меньшего приёмочного числа С (или равного ему), от значения параметра a. По графической зависимости р=(d<С)=f(а) и  определяем n:

         a=nQ – математическое ожидание случайной величины – числа d отказавших изделий.

         n=a/q=3,7/(1-0.75)=2.3/0.25=15шт.

6. Определение МПИ для своего прибора (курсовой проект) по методике для рабочих СИ.

1.) Определяем первичный межповерочный интервал по формуле для вновь разработанных СИ:

, где

- межповерочный интервал, (в годах);

- средняя наработка на метрологический отказ;

- требуемый уровень метрологической надёжности, выбирается из ряда 0.80.95 (0.95-стандарт).

2.) Определяем среднюю наработку на метрологический отказ:

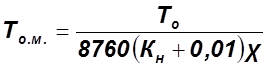, где

- средняя наработка на отказ;

- коэффициент использования;

- коэффициент метрологических отказов;

         Значения коэффициентов выбираются из таблицы для измерителя напряжения.

3.) Определяем среднюю наработку на  отказ:

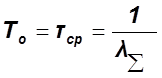, где

- интенсивность отказов;

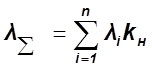, где

-коэффициент нагрузки, выбирается из ряда 0.5 – 0.7;

- интенсивность отказов i-го элемента;

_транз =0.15*10^-5                              _ист=0.3*10^-5 

_R=0.1*10^-5                                    _усил=0.05*10^-5 

_C=0.2*10^-5                                   _форм=0.5*10^-5 

_L=0.3*10^-5                                                         _вибр=0.5*10^-5 

_перекл=0.02*10^-5                                                          _{предохр}=0.03*10^-5 

_пуск=3.0*10^-5                                _счёт=0.001*10^-5 

_индик         =0.1*10^-5                                                 _деш=0.001*10^-5 

Тогда, суммарная интенсивность отказов:

=(3*0.15+19*0.1+7*0.2+1*0.3+2*0.02+2*3.0+1*0.1+1*0.3+1*0.3+4*0.05+3*0.5+2*0.5+1*0.03+10*0.001+5*0.001) *10^-5 * 0.7=9.5*10^-5;

Требуемая вероятность метрологического отказа:

;

;

;

;

.

Средняя наработка на отказ:

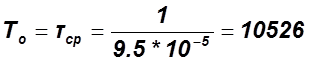часов.

Средняя наработка на метрологический отказ:

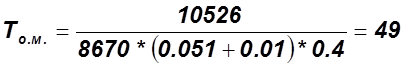лет.

МПИ:                               лет.

7.  Определение достоверности методики выполнения измерений параметров прибора.

1.) Определяем методическую достоверность:

Р(М)=n/m, где

m – общее количество, необходимое для проверки;

n – количество поверяемых параметров;

Р(М)=1.

2.) Определяем инструментальную достоверность:

Р(Q)=[1-()], где

- вероятность забракования годного прибора;

- вероятность признания годным бракованного прибора;

2.1) Определяем по таблице значений и  для нормального закона распределения:

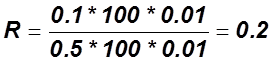
=0.013

=0.011

Р(Q)=[1-(0.013+0.011)]=0.976

3.) Определяем достоверность оператора (выбираем из ряда):

Р(L)=(0.9;0.95;0.97;0.99)=0.97

4.) Определяем достоверность методики выполнения измерений:

Рмви=Р(М)*Р(Q)*Р(L)=0.97*1*0.976=0.946

Заключение

В домашнем задании были получены навыки расчёта вероятности безотказной работы системы по экономическим показателям, вероятности безотказной работы блоков методом “Сверху вниз”, вероятности безотказной работы двух  структур; рассчитана система массового обслуживания (СМО), объём представительной выборки для испытания на надёжность, определён межповерочный интервал (МПИ) для вновь созданного прибора (из курсового проекта), определена достоверность методики выполнения измерений (МВИ).