Цифровая фильтрация основана на положениях математической теории линейных систем, преобразующих непрерывные сигналы. Линейная стационарная система преобразует непрерывный входной сигнал x(t) таким образом, что на её выходе возникает сигнал y(t), равный свёртке функции x(t) и импульсной характеристики системы h(t):
¥
y(t) = ò x(t - t) h(t) dt
- ¥
Цифровой фильтр – это дискретная система, поэтому его выходной последовательностью будет дискретная свёртка входного сигнала и импульсной характеристики фильтра. Таким образом, m-й отсчёт выходного сигнала цифрового фильтра можно записать следующим образом:
m
ym = S xm-k hk
k=0
Иными словами, цифровой фильтр проводит операцию взвешенного суммирования m предыдущих значений входного сигнала, причём роль последовательности весовых коэффициентов играют отсчёты импульсной характеристики фильтра [1].
В зависимости от того, как используется информация о прошлых состояниях системы, цифровые фильтры делятся на рекурсивные и нерекурсивные (трансверсальные). Нерекурсивным называется цифровой фильтр, использующий предшествующие отсчёты только входного сигнала. Рекурсивный фильтр использует предыдущие отсчёты не только входного, но и выходного сигнала. Рекурсивный цифровой фильтр является дискретным аналогом динамической системы с обратной связью и, реагируя на входной сигнал, может образовывать выходную последовательность бесконечной длины, играющую роль свободных колебаний. При неправильном выборе коэффициентов фильтра эти колебания могут иметь возрастающую амплитуду, что говорит о неустойчивости цифрового фильтра. Нерекурсивные цифровые фильтры не являются динамическими системами и устойчивы при любом выборе коэффициентов. Также важно отметить, что импульсная характеристика цифрового нерекурсивного фильтра содержит конечное число членов. Это свойство определяет применение нерекурсивных фильтров в программном обеспечении весов, так как реакция на скачок входного сигнала (помещение груза на платформу) всегда будет иметь известную конечную длительность.
В статических весах применяются фильтры низких частот (ФНЧ), так как полезный сигнал на частотной оси расположен возле нуля, а шумы и помехи располагаются по всему спектру (Рис. 5).
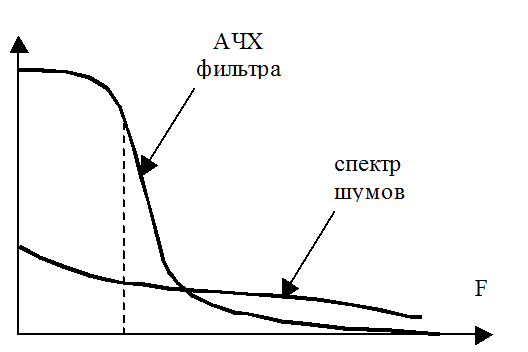
Рис. 5
При снижении частоты среза ФНЧ уменьшается уровень шумов на его выходе, однако при этом увеличивается время переходного процесса в фильтре (время установления показаний). Частота среза выбирается исходя из компромисса между этими двумя параметрами. Если компромисса достичь не удаётся, то применяется адаптивный фильтр. Алгоитм работы адаптивного фильтра следующий. Если входной сигнал изменяется медленно, то фильтр работает в обычном режиме. Когда изменение входного сигнала превышает некоторый порог, фильтр переключается на более высокую частоту среза или отключается вообще. После завершения переходного процесса фильтр возвращается в обычный режим (Рис. 6).
В динамических весах применение фильтров немного иное. Так как фаза взвешивания (Рис. 1) имеет определённую длительность, то для получения результата взвешивания достаточно проинтегрировать сигнал веса на протяжении 2-й фазы. Для этого нужно надёжно идентифицировать моменты заезда и съезда транспортного средства с платформы. Наиболее оптимальным фильтром для этой цели оказался полосовой фильтр с пологой АЧХ в области низких и высоких частот (Рис. 7). Верхняя частота среза подобрана так, чтобы отфильтровывать скачки и выбросы, возникающие в моменты заезда или съезда, а нижняя частота среза равна примерно половине верхней, чтобы получившаяся колебательная система имела невысокую добротность.

Рис. 6
На выходе такого фильтра сигнал имеет форму колоколообразных импульсов, по максимумам и минимумам которых определяются моменты заезда и съезда. Затем отбрасываются участки в начале и в конце интервала измерения (10…30%) и оставшиеся данные принимают участие в интегрировании.
Фильтры высоких частот (ФВЧ) обычно применяются в статических весах для выявления мешающих колебаний при взвешивании и служат обычно только для индикации нестабильности показаний.
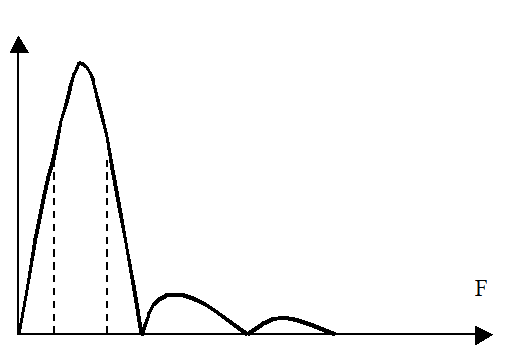
Рис. 7
При взвешивании в динамике могут найти применение полосно-заграждающие фильтры, если нужно подавить некоторый мешающий сигнал в заранее известной полосе частот (резонансные колебания платформы, раскачивание вагона на рессорах и т.д.).
Рассмотрим сигналы датчиков силы при движении груза вдоль платформы (взвешивание в динамике). Сила, приложенная к парам датчиков, изменяется почти линейно с течением времени (Рис. 8). Сумма неизменна в каждый момент времени и равна массе груза.

Рис. 8
Если весы построены по одноканальной или по многоканальной схеме, то сумма измерений по четырём каналам действительно будет неизменной. Если же используется схема с коммутацией каналов, то сумма будет зависеть от скорости и направления движения груза по платформе. Это вызвано тем, что измерения на каждом канале сдвинуты друг относительно друга на некоторое время, за которое успевает измениться вес, приходящийся на остальные датчики. Для того, чтобы устранить влияние неодновременности измерения по каналам на суммарный вес, нужно привести измерения на разных каналах к одному моменту времени. Это делается путём интерполяции. По двум (или трём) последовательным измерениям на каждом канале вычисляются коэффициенты интерполирующих прямых (парабол). Затем измерения на каждом канале приводятся к одному моменту времени. Линейная интерполяция эффективна при взвешивании груза, движущегося вдоль платформы. Квадратичная – при взвешивании колеблющихся грузов (жидкости или животные). Возможна также и экстраполяция на несколько отсчётов вперёд, например в системах дозирования, когда важно отследить достижение суммарным весом заранее определённого уровня.
1. С.И. Баскаков. Радиотехнические цепи и сигналы, 2-е изд. М.: Высш. шк., 1988-448 с.: ил.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.