Разделим
![]() на
на ![]() .
.
 Геометрический смысл
Геометрический смысл
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
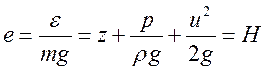
![]() Энергетический смысл: полная уд.эн.
в сечении = уд.пот.эн положения + уд.пот.эн давления + уд.кин.эн = полн.уд. энергия.
Энергетический смысл: полная уд.эн.
в сечении = уд.пот.эн положения + уд.пот.эн давления + уд.кин.эн = полн.уд. энергия.
При равномерном движении для всех точек в одном и том же сечении удельная потенциальная энергия будет одинакова.
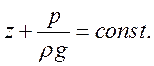 - выполняется при равномерном
движении.
- выполняется при равномерном
движении.
Удельная кинетическая энергия зависит от положения точки.
3.7 Уравнение энергии (ур. Д.Бернулли) для потока вязкой жидкости.
 Движение
установившееся в потоке, жидкость несжимаемая, уравнение неразрывности потока
выполняется в виде
Движение
установившееся в потоке, жидкость несжимаемая, уравнение неразрывности потока
выполняется в виде ![]() (жидкость капельная). В
сечениях 1 и 2 – равномерное движение, следовательно, поток имеет
цилиндрическую форму. В сечениях движение равномерное.
(жидкость капельная). В
сечениях 1 и 2 – равномерное движение, следовательно, поток имеет
цилиндрическую форму. В сечениях движение равномерное.
Обозначим:
![]() - энергия, внесенная в отсек 1-2 за
время
- энергия, внесенная в отсек 1-2 за
время ![]() через сечение-1;
через сечение-1; ![]() - энергия, вышедшая из отсека 1-2 за
время
- энергия, вышедшая из отсека 1-2 за
время ![]() через сечение-2;
через сечение-2; ![]() - потеря энергии в отсеке 1-2 между
сечениями 1-2.
- потеря энергии в отсеке 1-2 между
сечениями 1-2.
![]()
 через
некоторое сечение за
через
некоторое сечение за ![]() проходит энергия.
проходит энергия.
Через
dA за ![]() проходит
энергия
проходит
энергия ![]()
![]() - расход
- расход
![]() - объем
- объем
![]()
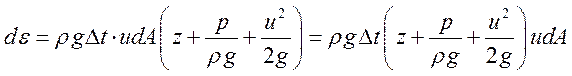
Находим
энергию, прошедшую через площадь ![]() за
за ![]() проходит
проходит ![]() .
Интегрируем по сечению.
.
Интегрируем по сечению.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
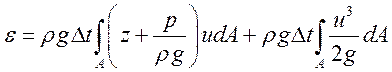
Действительная
КЭ – КЭ(![]() )
)
Условная
КЭ – КЭ(![]() ) – кинетическая энергия, посчитанная
по средней скорости.
) – кинетическая энергия, посчитанная
по средней скорости.
Пусть
![]() ,
тогда
,
тогда 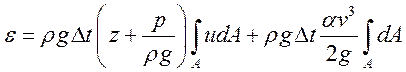
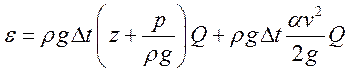
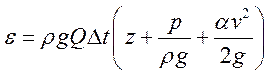 , где
, где ![]() -
вес жидкости, прошедшее через сечение за время
-
вес жидкости, прошедшее через сечение за время ![]() .
.
![]() , где
, где ![]() -
расстояние.
-
расстояние.
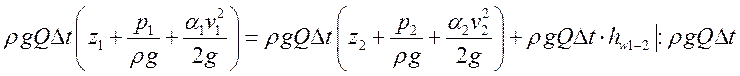
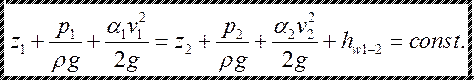 (уравнение Бернулли) уравнение
энергии для потока вязкой жидкости.
(уравнение Бернулли) уравнение
энергии для потока вязкой жидкости.
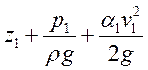 - это
- это ![]()
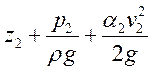 - это
- это ![]()
![]() - это
- это ![]() ,
следовательно
,
следовательно ![]() - полная энергия напора
между сечениями 1 и 2 или потеря полной удельной энергии между теми же самыми
сечениями.
- полная энергия напора
между сечениями 1 и 2 или потеря полной удельной энергии между теми же самыми
сечениями.
![]() .
.
![]() - коэффициент КЭ (коэфф. Кориолиса)
- коэффициент КЭ (коэфф. Кориолиса) ![]() - в практических расчетах
- в практических расчетах ![]() .
.
Условия применимости уравнения Бернулли.
Следствие из уравнения Бернулли:
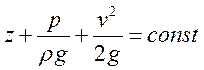 ;
;![]() ,
,
![]() - переменные величины;
- переменные величины;
Увеличение скорости ведет к уменьшению давления, уменьшение скорости ведет к увеличению давления.
Энергетический смысл уравнение Бернулли:
Полная удельная энергия нижележащего сечения ниже полной удельной энергии вышележащего сечений.
Полный напор нижележащего сечения меньше полного напора вышележащего сечения на величину полного напора.
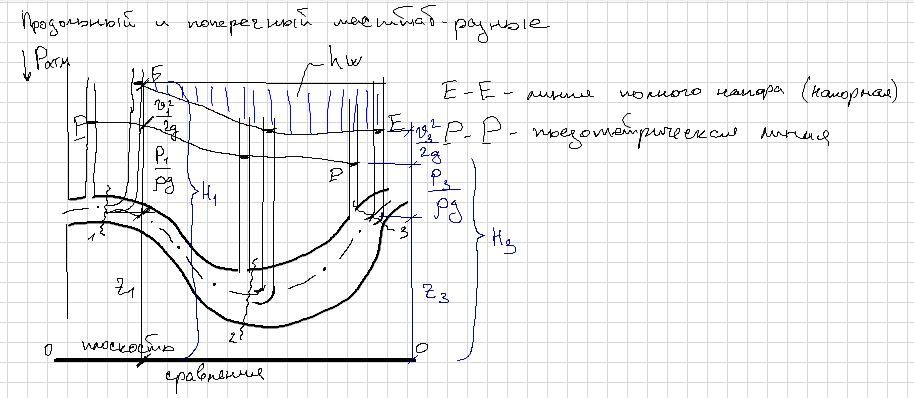
Гидравлический уклон – уклон наклонной линии – падение полного напора, приходящееся на единицу длины.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.