Расчеты по второй группе предельных состояний

3.2.2.5 Расчеты по второй группе предельных состояний.

Для недопущения предельных состояний второй группы в соответствии с нормами проектирования мостовых конструкций производятся расчеты по трещиностойкости и по деформациям.

                  Ко всем железобетонным конструкциям, в зависимости от их вида и назначения, принимаемой арматуры и условий работы, предъявляются определенные требования по трещиностойкости. Эти требования нормами проектирования  разделены на три категории, которые характеризуются допускаемыми значениями напряжений в бетоне и предельно допустимой шириной раскрытия трещин.

                  Мостовые конструкции из обычного железобетона рассчитывают с учетом требований по категории трещиностойкости 3в, которыми допускается раскрытие трещин ограниченной ширины. Нормами проектирования установлено два вида расчетов по трещиностойкости: по раскрытию трещин и по образованию трещин.

                  Расчет по раскрытию трещин сводится к выполнению условия:

                                                                                         ,                                                                                                     (3.63)

т.е. ширина раскрытия трещины a_cr должна быть не более допустимой , равной 0,02.

                  Ширину раскрытия трещин a_cr определяют по тем же зависимостям, что и в расчетах плиты балластного корыта. Необходимы лишь некоторые уточнения по определению площади зоны взаимодействия A_r в формуле (3.33).

                  Рабочая продольная арматура балки практически всегда располагается в несколько рядов. Зона взаимодействия ограничивается горизонтальной линией, проводимой на расстоянии радиуса взаимодействия r=6d от ближайшего к ней ряда стержней. Но если площадь всех стержней в этом ряду меньше половины площади сечений стержней в каждом из последующих рядов, то расстояние до границы зоны взаимодействия откладывают от предыдущего ряда (рис. 3.20). Кроме того, рабочая арматура балки может применяться в виде пучков. При армировании группами из двух стержней, коэффициент  в формуле (3.33) принимают равным 0,85, а при армировании группами из трех и более стержней – равным 0,75.

                          

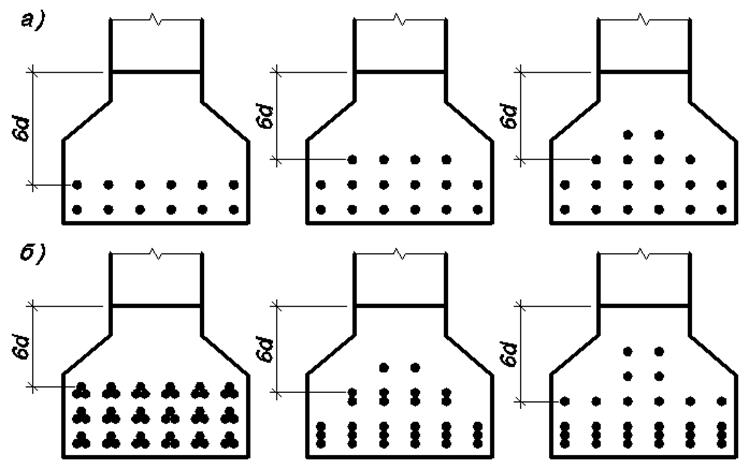
Рис 3.20.  Схема к определению площади зоны взаимодействия арматуры с бетоном:

а –  для одиночных стрежней; б – для пучков

            Зона взаимодействия не должна выходить за нейтральную ось сечения.

                  Расчет по образованию продольных трещин в главной балке делается так же, как и в плите балластного корыта.

                  Наклонные сечения балок из обычного железобетона рассчитывают только по раскрытию трещин, т.е. должно выполняться условие (3.63). Допускаемая ширина раскрытия трещин  принимается такой же, как и для нормальных трещин, т.е. равной 0,02 см. Ширину раскрытия трещины определяют по формуле 3.32, а напряжения в отгибах, хомутах и продольной арматуре стенок (ребер) при этом подсчитывают  по формуле:

,

где - коэффициент, учитывающий перераспределение напряжений в зоне образования наклонной трещины; -касательные напряжения в бетоне на уровне центра тяжести приведенного сечения; -коэффициент армирования стенки на участке наклонной трещины.

                                                     ,                                    (3.64)

где            A_si, A_sw, A_sl – соответственно площадь одного отогнутого стержня, одного стержня хомута, одного продольного стержня;  - соответственно углы наклона отогнутых стержней продольной рабочей арматуры, хомутов, продольных стержней к рассматриваемому наклонному сечению;               b – ширина ребра на уровне центра тяжести сечения; l_i – длина предполагаемой наклонной трещины.

                  Длину наклонной трещины l_i в двутавровых балках измеряют между вутами поясов (рис. 3.21), в тавровых – от ближайшего к нейтральной оси ряда растянутой рабочей арматуры до начала вута верхнего пояса.

                  Направление наклонной трещины принимают перпендикулярным главным растягивающим напряжениям в центре тяжести приведенного сечения. Угол φ между главными растягивающими напряжениями и осью балки определяется из условия:

                                                                                         ,                                                               (3.65)

где             - нормальные и касательные напряжения в центре тяжести плоского вертикального сечения;  - нормальные напряжения по горизонтальной площадке в той же точке.

                  Так как в балках из обычного железобетона на уровне оси, проходящей через центр тяжести приведенного сечения, , а  мало, то из формулы (3.65) следует, что , следовательно, наклонную трещину следует принимать направленной под углом 45⁰ к оси балки. Если наклонные стержни отогнуты под углом 45⁰, то , .

                  Значение коэффициента  подсчитывают по формуле:

.

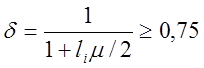                  Величину радиуса армирования R_r при определении коэффициента раскрытия трещин  определяют по формуле:

,

где,           - коэффициенты, учитывающие степень сцепления арматурных стержней с бетоном;  - соответственно число наклонных стержней, хомутов и продольных стержней в пределах наклонного сечения;   - диаметры соответственно наклонных стержней, хомутов и продольных стержней;  - то же, что и в формуле (3.64).

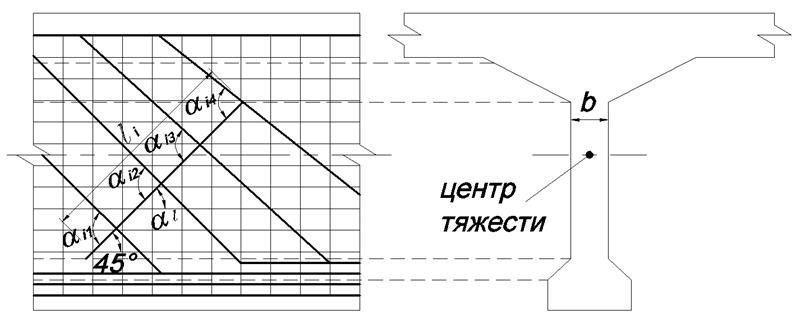
Рис.3.21. Схема к определению ширины раскрытия наклонной трещины

                  Расчет по деформациям (по ограничению прогибов) сводится к выполнению условия:

                                                                                         ,                                                                                                 (3.66)

где            f_0,5 – прогиб в середине пролета, вызываемый временной вертикальной нагрузкой;

           f_пред – предельный допускаемый прогиб, подсчитываемый по формуле:

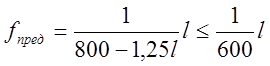                                                               ,                                                                           (3.67)

где            l – расчетный пролет, м.

                  Для однопролетных мостов f_пред увеличивают на 20%.

                  Прогиб в середине пролета подсчитывают по формуле:

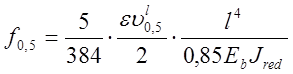                                                                       ,                                                                    (3.68)

где             - коэффициент, исключающий из нагрузки редко обращающиеся тяжелые транспортеры; - временная эквивалентная нагрузка на пролетное строение; - момент инерции приведенного сечения.

                  Коэффициент 0,85 учитывает влияние трещин на жесткости сечений. Кроме того, для бетонов, подвергнутых тепловлажностной обработке, которую при изготовлении конструкций заводского и полигонного изготовления применяют всегда, величина модуля упругости бетона уменьшается на 10%, т.е. к величине E_b в формуле (3.68) вводят дополнительный коэффициент, равный 0,9.