



3.3.5. Проверка прочности, устойчивости формы и трещиностойкости бетонных опор.
Опора моста с
позиций строительной механики представляет собой стержень, сжимаемый продольной
силой. При этом стержень всегда считается сжатым внецентренно, так как
учитывается случайный эксцентриситет ![]() , по СП
35.13330.2011 принимаемый равным:
, по СП
35.13330.2011 принимаемый равным:
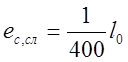
где l0 – расчетная (свободная) длина элемента.
Расчетная (свободная) длина сжатого элемента зависит от способов закрепления его концов. На рис. 3.32 приведены возможные схемы закрепления концов стержня и соответствующие этим схемам расчетные (свободные) длины. Работа сжатых элементов опор, строго говоря, не соответствует ни одной из показанных на рисунке схем. Ориентироваться нужно на такую схему, которая наиболее бы приближалась к фактической работе опоры. По нормам проектирования при применении опорных частей каткового и секторного типа взаимную связь соседних опор не учитывают и расчетную длину l0 принимают равной двум высотам опорам. Это является допущением: в опорных частях возникают силы трения, поэтому какая-то связь между соседними опорами существует всегда. Такое же допущение можно принять и при тангенциальных и плоских опорных частях, хотя в этом случае оно является более грубым. Неучет сил трения в опорных частях мало сказывается на определении расчетной (свободной) длины опоры, тем более, что получаемые при этом результаты расчетов идут в запас прочности. Таким образом, за расчетную схему опоры принимают стержень с жестко заделанным концом внизу и со свободным верхним концом. Высоту опоры в приводимых ниже расчетах по устойчивости формы измеряют от точки приложения к опоре опорных давлений, т.е. от верха подферменников до обреза фундамента.
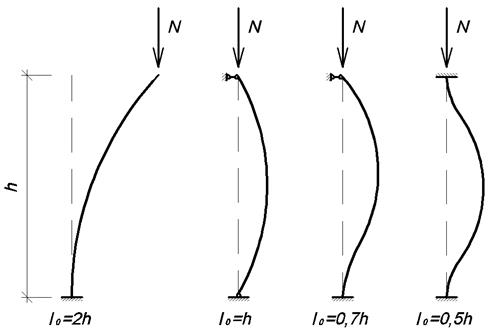
Рис. 3.32. Зависимость расчетной (свободной) длины стрежня от способа закрепления его концов
Расчетный
эксцентриситет ![]() определяют как сумму
эксцентриситетов, определимых из статического расчета
определяют как сумму
эксцентриситетов, определимых из статического расчета ![]() и
случайного
и
случайного ![]() , т.е.
, т.е.
![]()
Если
по результатам статического расчета в сечении получены изгибающий момент M и продольная
сила N, приложенные в
его центре тяжести, такое сечение считают внецентренно сжатым силой N, с
эксцентриситетом ![]() относительно оси,
проходящей через центр тяжести сечения.
относительно оси,
проходящей через центр тяжести сечения.
При действии внецентренно приложенной силы N верх опоры
получит некоторые отклонения от первоначального положения (рис. 3.33). Нормы
проектирования допускают упрощенный учет влияния прогиба на прочность сечения
путем умножения эксцентриситета ![]() на коэффициент
на коэффициент ![]() , подсчитываемый по формуле:
, подсчитываемый по формуле:
![]() ,
,
где Ncr – условная критическая сила, при достижении которой прямолинейная форма стержня перестает быть устойчивой.
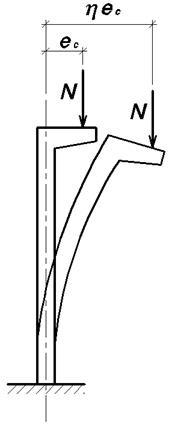
Рис. 3.33. Изменение эксцентриситета силы при внецентренном сжатии
В массивных опорах отклонение их верха в рассматриваемых случаях незначительно,
поэтому величина коэффициента ![]() близка к единице.
близка к единице.
Величину критической силы Ncr подсчитывают по формуле:
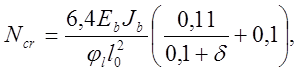
где
Eb – модуль
упругости бетона; Jb – момент инерции сечения;![]() – коэффициент, учитывающий влияние
длительно действующей нагрузки на прогиб элемента;
– коэффициент, учитывающий влияние
длительно действующей нагрузки на прогиб элемента; ![]() -
отношение расчетного эксцентриситета
-
отношение расчетного эксцентриситета ![]() к высоте сечения h, но не менее
величины
к высоте сечения h, но не менее
величины ![]() , подсчитываемый по формуле:
, подсчитываемый по формуле:
![]()
Величину
коэффициента ![]() подсчитывают по формуле:
подсчитывают по формуле:
![]()
где Ml – момент, равный произведению силы Nl от постоянных нагрузок на расстояние от линии действия силы Nl до наименее сжатой грани сечения; M – то же от постоянных и временных нагрузок.
Для невысоких массивных опор критическая сила может быть подсчитана по приближенной формуле:
![]()
![]()
Вводится ограничение положения силы N:
![]() , (3.87)
, (3.87)
где ac – расстояние от оси, проходящей через центр тяжести всего сечения, до наиболее сжатой грани.
Условие (3.87) должно исключить скол бетона, если сила N проходит достаточно близко к краю сечения у сжатой его грани. При невыполнении этого условия размеры сечения должны быть увеличены.
Условие прочности и устойчивости формы в общем виде:
![]() ,
,
где N – действующая в сечении продольная сила; Nпред – продольная сила, которую может воспринять сечение.
Внецентренно
сжатые бетонные элементы проверяют на прочность, когда продольная сила N выходит за
пределы ядра сечения, т.е. когда ![]() . Границы ядра
сечения определяют по формуле:
. Границы ядра
сечения определяют по формуле:
![]() ,
,
где Jb, Ab – соответственно момент инерции и площадь сечения; y– расстояние от центра тяжести сечения до его верха (или низа).
При проверке сечения на прочность, условие принимает вид:
![]() ,
(3.88)
,
(3.88)
где ![]() - площадь сжатой зоны сечения.
- площадь сжатой зоны сечения.
В расчетах по проверке прочности сечения приняты следующие допущения:
- бетон растянутой зоны полностью выключился из работы сечения;
- напряжения в сжатой зоне сечения одинаковы по всей ее площади и равны расчетному сопротивлению бетона Rb;
- равнодействующая усилий от внешних нагрузок N приложена в центре тяжести сжатой зоны сечения.
Для
элемента таврового сечения высотой h с толщиной полки
![]() при эксцентриситете силы N в сторону полки
(рис. 3.34,а), условие (3.88) принимает вид:
при эксцентриситете силы N в сторону полки
(рис. 3.34,а), условие (3.88) принимает вид:
![]() , (3.89)
, (3.89)
где
![]() - соответственно ширина ребра и
ширина полки;
- соответственно ширина ребра и
ширина полки; ![]() - толщина полки; x– высота сжатой
зоны.
- толщина полки; x– высота сжатой
зоны.
Расстояние а от линии действия силы N до сжатой грани равно:
![]()
При
![]() граница сжатой зоны проходит в
пределах ребра.
граница сжатой зоны проходит в
пределах ребра.
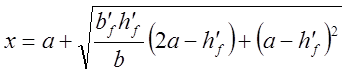 (3.90)
(3.90)
При
![]() (граница сжатой зоны проходит в плите) принимают в формулах b=bf, т.е. сечение
рассчитывают как прямоугольное шириной
(граница сжатой зоны проходит в плите) принимают в формулах b=bf, т.е. сечение
рассчитывают как прямоугольное шириной ![]() .
.
Для случая, когда эксцентриситет силы N направлен в сторону ребра (рис. 3.34,б), условие прочности принимает вид:
![]() , (3.91)
, (3.91)
а граница сжатой зоны x может быть подсчитана по формуле:
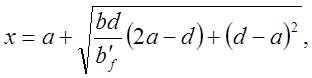 (3.91,а)
(3.91,а)
где
d=h-![]() .
.
При
![]() следует принять bf=b, при этом х=2а и сечение
рассчитывают как прямоугольное шириной b.
следует принять bf=b, при этом х=2а и сечение
рассчитывают как прямоугольное шириной b.
Формулы (3.90), (3.91,а) могут быть приведены к такому виду:
![]()
при эксцентриситете в сторону полки (в таком виде формула приведена в СП 35.13330.2011);
![]()
при эксцентриситете в сторону ребра.
Для
элементов прямоугольного сечения шириной b в формулах
(3.89) и (3.90) следует принимать ![]() и
и ![]() . Условие прочности принимает вид:
. Условие прочности принимает вид:
![]() , (3.92)
, (3.92)
при
этом ![]() .
.
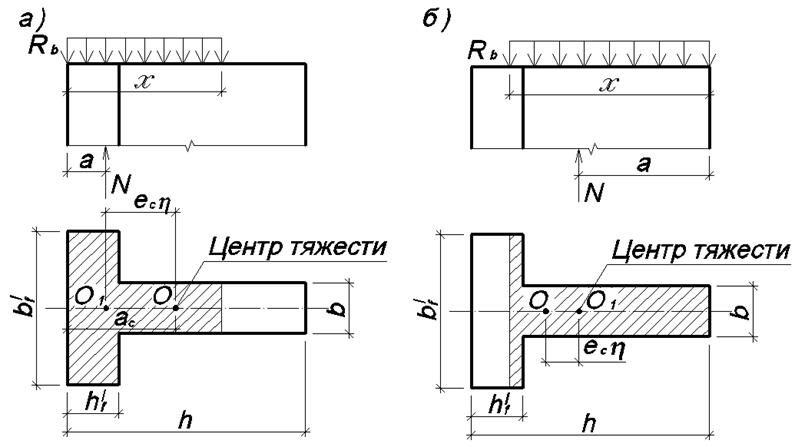
Рис. 3.34. Схемы к расчету бетонного сечения тавровой формы по прочности:
а – эксцентриситет сжимающей силы направлен в сторону полки; б – эксцентриситет сжимающей силы направлен в сторону полки
У опор, расположенных в пределах водотока, поперечное сечение принимают обтекаемой формы с заострением или закруглением в носовой и кормовой части (рис. 3.35).
Проверка устойчивости формы сводится к выполнению условия:
![]() , (3.93)
, (3.93)
где N – продольная сила, определенная для расчета по прочности; Rb – расчетное сопротивление бетона на осевое сжатие, Ab – общая площадь всего рассматриваемого сечения опоры; φ – коэффициент продольного изгиба, принимаемый по СП 35.13330.2011.
Трещиностойкость бетонных конструкций опор обеспечивается ограничением сжимающих напряжений в бетоне – это расчет по образованию продольных трещин. Такой расчет выполняют только для стадии эксплуатации. Условие трещиностойкости:
![]() , (3.94)
, (3.94)
где
![]() - расчетное сопротивление бетона для
расчетов по предотвращению образования в конструкции продольных трещин на
стадии эксплуатации.
- расчетное сопротивление бетона для
расчетов по предотвращению образования в конструкции продольных трещин на
стадии эксплуатации.
Если равнодействующая внецентренно сжимающих сил N проходит в пределах ядра сечения, то сжимающие напряжения в сечении определяют по известной формуле сопротивления упругих материалов:
![]() , (3.95)
, (3.95)
где Ab, Jb – соответственно площадь и момент инерции сечения; ec – расстояние от линии действия силы N до центра тяжести сечения; х – расстояние от центра тяжести сечения до наиболее напряженной грани элемента.
Если
сила N выходит за
пределы ядра сечения, при определении ![]() ,
принимают следующие допущения (рис.3.36):
,
принимают следующие допущения (рис.3.36):
- сжатый бетон работает упруго, справедлива гипотеза плоских сечений;
- растянутый бетон полностью выключился из работы сечения.
Для элементов прямоугольного сечения шириной b, если сила N приложена на расстоянии а от сжатой грани опоры:
![]() ,
(3.95,а)
,
(3.95,а)
где x=3а – высота сжатой зоны.
Рекомендации для определения ![]() в элементах
таврового сечения, когда ec>r, приведены в
учебном пособии [ 2 ].
в элементах
таврового сечения, когда ec>r, приведены в
учебном пособии [ 2 ].
Силу N в формулах (3.95), (3.95,а) определяют как для расчетов по второй группе предельных состояний.
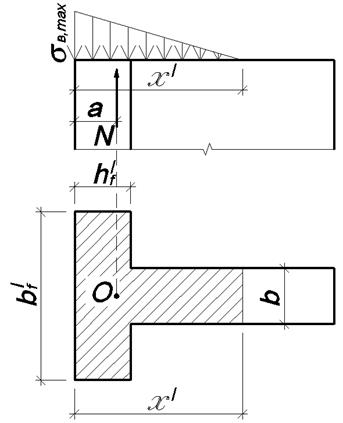
Рис. 3.36. Схема к расчету бетонных опор по трещиностойкости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.