Проверка основного закона динамики вращательного движения

Лабораторная работа № 4

Проверка основного закона динамики вращательного движения.

Приборы и принадлежности: маятник Атвуда (крестовина с грузами), измерительная рулетка, секундомер, штангенциркуль.

Введение

Основной закон динамики вращательного движения вокруг некоторой оси имеет вид

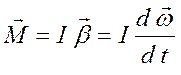                         (1)

где М – вращающий момент, произведение вращающей силы на плечо (более подробно М определённо в лабораторной работе №2), β – угловое ускорение;

I – момент инерции тела относительно оси вращения.

Под плечом силы относительно точки 0 понимают длину перпендикуляра, опущенного из точки 0 на прямую, вдоль которой действует сила .

  

Рис. 1

Моментом инерции материальной точки относительно данной оси вращения называется произведение массы этой точки на квадрат расстояния от нее до данной оси вращения.

Обозначим массу материальной точки m_I, расстояние её от оси вращения r_I ; момент инерции её относительно оси вращения: m_I r_I².

Моментом инерции I твёрдого тела относительно какой – либо оси называется сумма моментов инерции всех материальных точек данного тела относительно той же оси .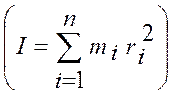

Момент инерции тела в динамике вращательного движения играет такую же роль, как масса тела в динамике поступательного движения, то есть является мерой инерции тела и характеризует распределение масс относительно оси вращения.

Из уравнения (1) следует, что ускоре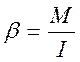ние , сообщаемое телу вращающим моментом, зависит от момента инерции тела: чем больше момент инерции, чем больше I, тем меньше угловое ускорение.

Отсюда следует, что, если вращающий момент М = const остаётся постоянным, то отношение угловых ускорений будет обратно пропорционально моментам инерции этих тел:

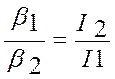                                  (2)

Целью настоящей работы является проверка основного закона динамики вращательного движения (1) на основе определения соотношение между угловыми ускорениями и моментами инерции (2).

Описание установки

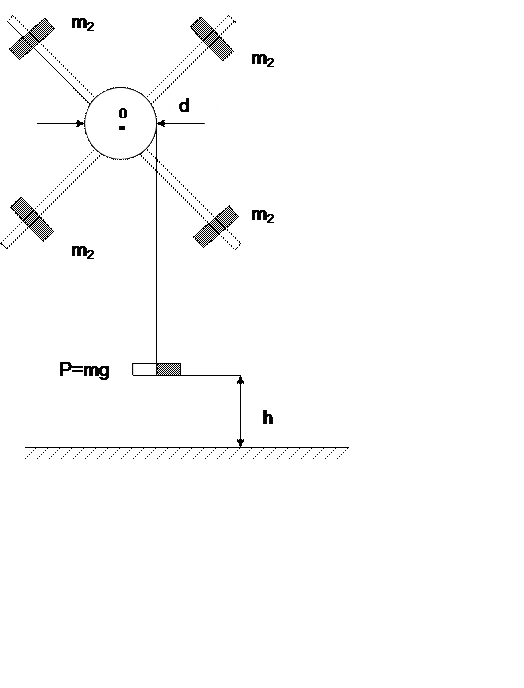
Основной частью прибора (см. рисунок) является крестовина с четырьмя одинаковыми грузами m_r (положение которых можно измерять относительно оси вращения) шкива прикрепленной к ней нитью, на конце которой может быть подвешена гирька Р (массой m). Когда груз Р, подвешенный к нити, опускается, нить разматывается и приводит всю систему в равноускоренное вращательное движение.

Если гирька Р будет находится на некоторой высоте от пола, то её потенциальная энергия E_n=m g h. Под действием силы тяжести маятник Атвуда начинает вращаться и потенциальная энергия гирьки Е_n переходит в кинетическую энергию поступательного движения W_k и кинетическую энергию вращающейся крестовины W_вр. При малости сил сопротивления на уровне пола будет справедливо следующее равенство:

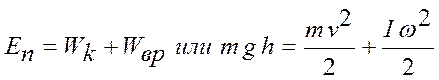                             (3)

Угловая скорость маховика  и линейная скорость V гирьки соответствуют моменту удара об пол, при этом .

Так как нить намотана на шкив, то очевидно, что скорость поступательного движения гирьки всегда равна линейной скорости вращающегося шкива, поэтому , где r – радиус шкива.

Используя формулу для равноускоренного движения без начальной скорости

.

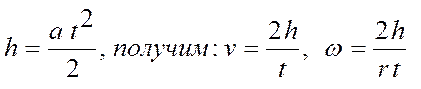Подставляя эти значения в формулу (3), получаем 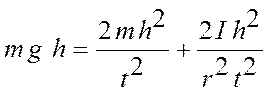, откуда момент инерции

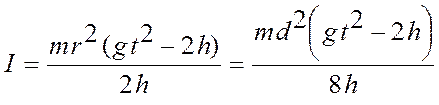                           (4)

В рабочую формулу (4) входят, величины измеряемые в опыте, и .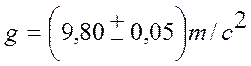

Момент инерции крестовины определяется для двух положений грузов m_r на концах стержней и на их середине при постоянном вращающем моменте.

В этом случае выполняется соотношение (2).

     Принимая во внимание, что линейное ускорение точки связано с угловым ускорением соотношением a=β r, определим линейное ускорение гирьки для двух положений грузиков на крестовине:

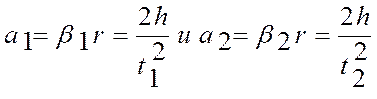
тогда уравнение (2) можно преобразовать к виду

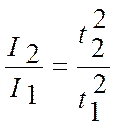                                                                                     (5)

и проверка основного закона динамики вращательного движения сводится к проверке выполнения равенства (5).

Порядок выполнения работы

1. Поместить грузы m_r на концы стержней до отметки, при этом следует тщательно закрепить и симметрично установить грузы относительно оси вращения.
2. Взвесить подвешенную к нити гирьку Р, поднять её до отметки на высоту порядка 1,5м. Нить при этом намотать на шкив.
3. Отпустить всю систему и одновременно включить секундомер. В момент, когда гирька коснётся пола, остановить секундомер. Измерить время и высоту падения не менее трёх раз и за окончательный результат взять среднее значение.
4. С помощью штангенциркуля измерить диаметр шкива d 3 раза.
5. Передвинуть грузы m_r на середину стержней, поднять ту же самую гирьку на ту же высоту и повторить измерения согласно пунктам 1–3; результаты измерений записать в таблицу.

№ п/п

m

Δm

h

Δh

d

Δd

t1

Δt1

t2

Δt2

кг

м

с

1 2 3

6. Подставить  в формулу (4) и определить моменты инерции I₁ , I₂; проверить равенство (5), для чего найти .
7. Определить относительную и абсолютную погрешности момента инерции маятника, результаты измерений представить в виде:

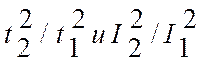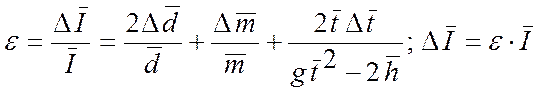
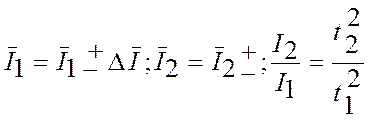
Контрольные вопросы 1

1.  Что называется моментом инерции материальной точки?

2.  В чем физический смысл момента инерции?

3.  Как математически выражается основной закон динамики вращательного движения?

Контрольные вопросы 2

1.  Сравните основные характеристики кинематики и динамики поступательного и вращательного движений.

2.  Напишите закон сохранения энергии применительно к маятнику Атвуда.

3.  К чему сводится в данной работе проверка основного закона динамики вращательного движения?

Литература

1.  Трофимова Т.И. Курс физики. – М., 1993.

2.  Грабовский Р.И. Курс физики. – М., 1980. §21.

3.  Засман Г.А., Тодес О.М. Курс общей физики. – М., 1967. Т.1, §11.

4.  Савельев И.В. Курс общей физики. – М., 1977. Т.1, §38.