Определение ускорения свободного падения с помощью физического маятника

                                             Лабораторная работа №6.

                       Определение ускорения свободного падения с помощью       

                                        физического маятника.

Цель работы: Изучение гармонических колебаний и определение ускорения свободного падения на примере физического (оборотного) маятника.

Приборы и принадлежности: Оборотный маятник, Таймер- секундомер, линейка.

ВВЕДЕНИЕ

Рассмотрим в качестве примера гармонических колебаний физический маятник. Общее понятие гармонических колебаний и их характеристики определены во введении к лабораторной  работе №5.

Физическим маятником называется твердое тело, совершающее колебания под действием силы тяжести относительно неподвижной оси, не проходящей через центр масс.

На тело (см.рис.1) относительно оси вращения 0 действует вращающий момент силы тяжести М=mga  sin j, в результате чего оно совершает вращательно- колебательное движение.

Уравнение динамики вращательного движения   в данном случае

                            -mga sin j =I j,                                     (1)

где I- момент инерции тела относительно оси вращения; а - расстояние от оси вращения до центра масс; знак «минус» в формуле (1)  указывает на то, что момент вращающей силы противоположен по направлению угловому смещению, 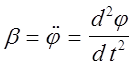  - угловое ускорение. Для малых углов отклонения sin »j и уравнение (1) принимают вид дифференциального уравнения свободных гармонических колебаний:

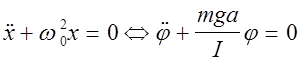                                           (2)

где роль смещения играет угол отклонения j, а круговая частота .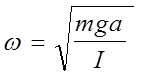

Таким образом, движение физического маятника при малых углах отклонения представляет собой гармонические колебания вблизи положения равновесия.

,  с частотой и периодом колебаний соответственно        

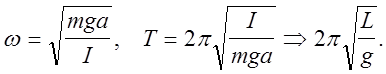                                  (3)

        Величина 1/ma имеет размеренность длин и, если ее обозначить за L=I/ma, то формула (3) сведется к формуле периода колебаний математического маятника. Отсюда следует смысл величины L, называемой приведенной длиной. Приведенная длина физического маятника равна длине такого математического маятника, период колебаний которого совпадает с периодом колебаний физического. Формула (3) является основой для определения ускорения свободного падения при известных значениях периода и приведенной длины. Для определения приведенной длины используется метод оборотного маятника, суть которого состоит в следующем. Обозначим период колебаний физического маятника относительно точки 0 (рис.1) за Т₁ затем выберем на прямой ОС точку В (при условии, что ОВ>С). Если перевернуть маятник и провести ось вращения через точку В, то период колебания в общем случае изменится и примет некоторое значение Т₂. Согласно формуле (3), периоды Т₁ и Т₂ соответственно

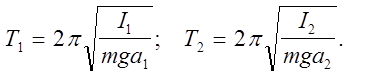                                     (4)

Перемещая оси вращения вдоль прямой ОВ, можно добиться того, что периоды колебаний будут совпадать. Покажем, что в этом случае расстояние между осями (ОВ) будет равно приведенной длине. Итак, при Т₁=Т₂ имеем:

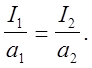                                                                                      (5)

Используя теорему Штейнера, выразим моменты инерции I₁ и I₂ через момент инерции тела относительно центра масс I₀.

                                                      (6)

Подставляя выражения (6) в формулу (5). Находим

                                          I₀=ma₁a₂,                                             (7)

и, окончательно, используя формулы (7) и (6), для приведенной длины получим

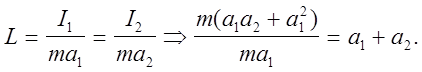                                   (8)

                                         Описание прибора.

     Оборотный маятник состоит из металлического стержня длиной более метра с миллиметровыми делениями на поверхности (см. рис.2). На стержне укрепляются две передвижные опорные призмы Q₁ и Q₂ и грузы А и D.

Подвешивая маятник то за одну, то за другую призму, можно добиться путем перемещения призм и грузов равенства периодов. В этом случае расстояние между призмами, как показано выше, является приведенной длиной, а период колебаний определяется формулой  .

откуда находим 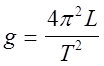                       .                                 (9)

     Так очень трудно или даже невозможно достичь полного равенства периодов, то практически добиваются того, чтобы разность между ними была минимальна. Вследствие этого, при вычислении ускорения силы тяжести в формулу (9) вместо Т подставляют среднее значение Т₁ и Т₂. Расчетная формула для q окончательно принимает вид

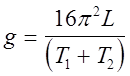                                 .                                             (10)

                                 Порядок выполнения работы.

1.  Подвесить маятник на призме Q₁ и замерить секундомером время не менее 50 колебаний t₁, определить период колебаний Т₁=t₁/50.

2.  Перевернув и подвесив маятник на призму Q₂ определить период Т₂ ( ни призмы, ни грузов в процессе измерений не перемещать, т.к. они заранее установлены в соответствии с минимумом Т₂- Т₁).

3.  Измерить расстояние между призмами.

4.  Измерение каждого периода проводится не менее трех раз. По данным измерениям рассчитать среднее значения Т₁ и Т₂ и их абсолютные погрешности DТ₁ , DТ. 

хi	L (м)	DL(м)	Т1(с)	Т2(с)	DТ1(с)	DТ2(с)
1. 2. 3.

6.  По формуле (10) рассчитать значение q в системе СИ, а по формулам (11), (12) рассчитать относительную и абсолютную погрешности.

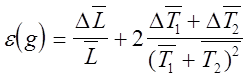                                     ,                                 (11)

                                                                                          (12)

7.  Записать ответ в виде

                                           m/c².

                                         Контрольные вопросы I.

1.  Напишите уравнение гармонических колебаний и дайте определение их характеристик.

2.  Дайте определение физического маятника.

3.  Напишите формулу периода колебаний физического маятника и объясните, от чего он зависит.

4.  Что такое приведенная длина, в чем ее физический смысл?

                                        Контрольные вопросы II.

1.  Получите дифференциальное уравнение колебаний физического маятника и формулу периода.

2.  Объясните смысл метода оборотного маятника.

3.  Объясните, когда и почему приведенная длина физического маятника равна расстоянию между призмами.

                                               Литература

1.  Зисман Г.А., Тодес О.М. Курс общей физики, М. 1967 г. Т.1, п.51.

2.  Грабовский Р.И., Курс общей физики, М. 1980 г.. п.29.

3.  Савельев И.В. Курс общей физики. М. 1971 г.п.67.