Изучение вынужденных колебаний в колебательном контуре

ЛАБОРАТОРНАЯ РАБОТА №62

ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Приборы: генератор ГЗ-112/1, кассета ФПЭ-11/10, магазин R, магазин С, осциллограф.

1.  Свободные колебания в контуре без активного сопротивления

Цепь, содержащая катушку индуктивности L и конденсатор емкостью С, называется колебательным контуром. Зарядим обкладки конденсатора зарядом

q₀ , при этом контур будет обладать энергией

,

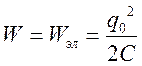которая локализована в электрическом поле конденсатора.

t=0

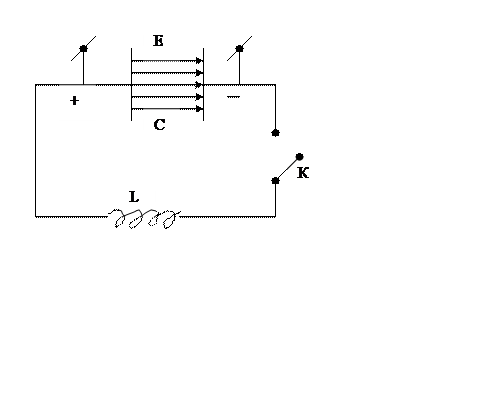
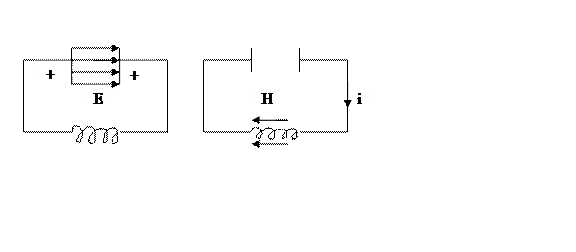
Пусть сопротивление контура R=0. Затем контур ключом К. Конденсатор начнет разряжаться, но ток в контуре будет нарастать постепенно вследствие явления самоиндукции в катушке L. Последовательные стадии колебательного процесса: изменения заряда на обкладках конденсатора и тока в цепи – изображены на рисунке.

t=T/4

t=0

	T=T/2, 1=0

 

	t = T
			T = 3/4T

 

В колебательном контуре происходят колебания заряда на обкладках конденсатора и тока в цепи, а энергия электрического поля конденсатора превращается в энергию магнитного поля катушки и наоборот. По второму правилу Кирхгофа можно написать для контура:

, где 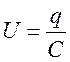 - падение напряжения на конденсаторе,

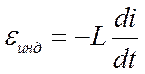     -ЭДС самоиндукции в катушке.

     

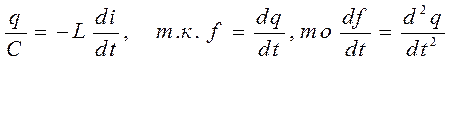
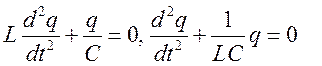        -дифференциальное уравнение незатухающих колебаний заряда в контуре. Оно аналогично уравнению гармонических колебаний материальной точки массой m под действием упругой (или квазиупругой) силы:  

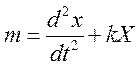
Решение дифференциального уравнения для колебательного контура будет иметь вид:

    

1= -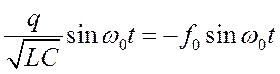

при начальных условиях   при t=0.

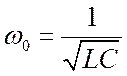  - круговая (циклическая) частота колебаний.  Период колебаний в идеальном контуре (R=0) определяется формулой Томсона . Частота колебаний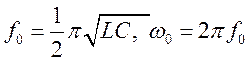

График функций  и  показан на рис.1

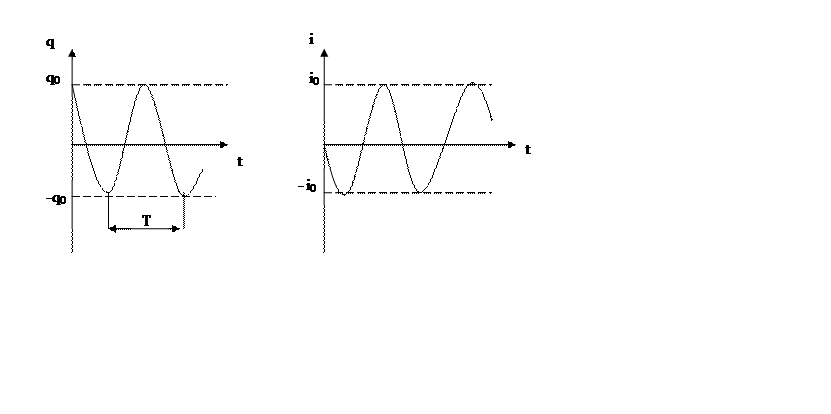
Рис.1

2.  Затухающие колебания

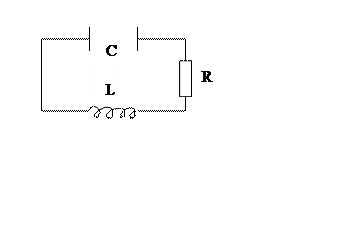
Всякий реальный контур обладает активным сопротивлением  .

Энергия, запасенная в контуре, постепенно расходуется в активном сопротивлении на нагревание по закону Джоля-Ленца, вследствие чего свободные колебания затухают.

3. Вынужденные колебания

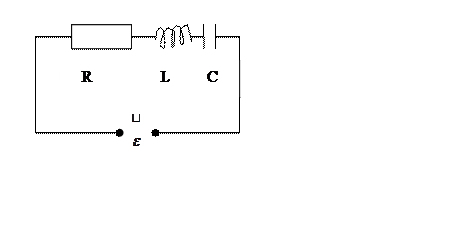
Чтобы сделать электрические колебания в реальном контуре незатухающими, включим последовательно с элементами контура источник переменной ЭДС вида:

Сумма падений напряжений на элементах контура равна приложенной ЭДС

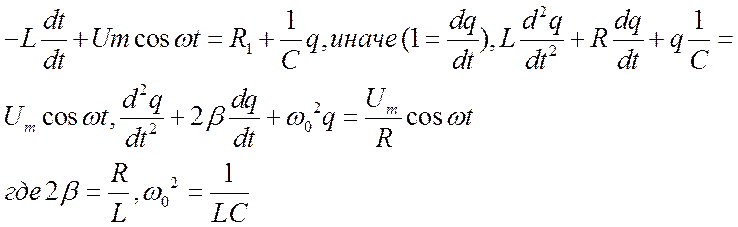
Получим дифференциальное уравнение вынужденных колебаний в колебательном контуре, сходное с уравнением вынужденных механических колебаний. Решение этого уравнения в установившемся режиме можно представить в виде:

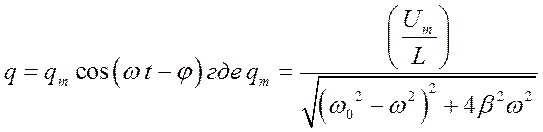      или

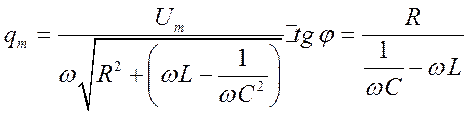
Для тока

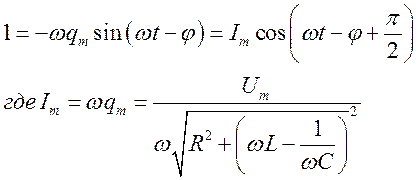
В таком контуре возможно явление резонанса - резкое увеличение амплитуды тока. Когда частота переменной ЭДС становиться равной резонансной частоте:

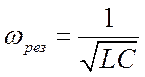
Собственная частота контура равна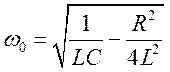

откуда следует, что резонанс наступает при частоте 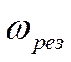. Несколько большей, чем  .

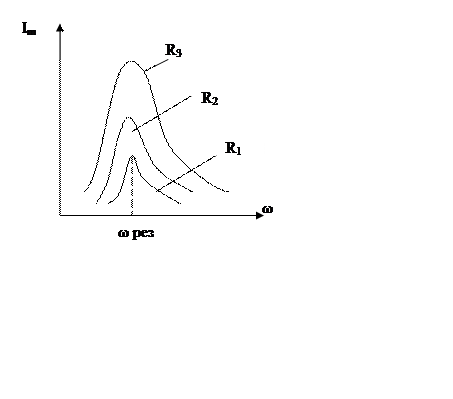Рис.2

Чем меньше R, тем ближе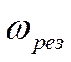 к .Пик резонансной кривой увеличивается с уменьшением R (рис.2). Таким образом, контур с малым затуханием дает острый резонанс. Это позволяет в случае сложного характера вынуждающей ЭДС настраивать такой контур на отдельные гармонические составляющие ЭДС. Пусть внешняя ЭДС может быть представлена в виде суммы косинусоид:

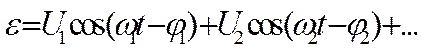
Подберем емкость С и индуктивность L так, чтобы   .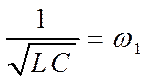

Тогда условие резонанса будет выполняться только для составляющей   Непрерывно меняя С или L контура, можно заставить его последовательно отзываться на все частоты   проводя таким образом гармонический анализ сложного колебания. Обратный процесс используется в современных синтезаторах звука. Итак, цель работы- изучить резонанс в колебательном контуре.

4.  Блок-схема установки

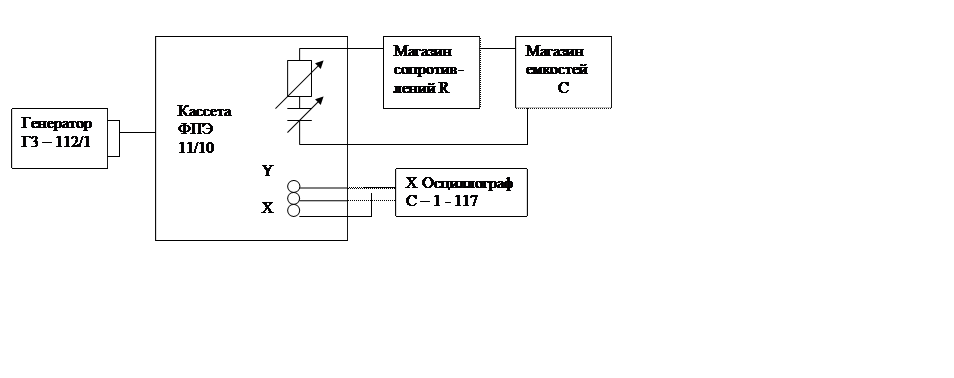
Описание установки: генератор выдает синусоидальный сигнал на кассету, состоящую из

индуктивности L, переменной емкости С переменного сопротивления С сопротивления R сигнал поступает на осциллограф.

Порядок выполнения работы

·  Установить на генераторе тумблер « _|         |_  , ~ » . в положение  « ~ » , лимб установки частоты на 14, множитель частоты на 10³, ослабление на 10, ручка плавного усиления – до упора вправо.

·  Установить на осциллографе переключатель «Синхро-режим» в положение Б, переключатель Время/дел – положение 1mS, переключатель V/дел – в положение 0,2 V, переключатель «Внутр. Внешн. Сеть» в положение «внешн.», переключатель «     __  ,     » в положение «~».

·  Установить на магазине сопротивлений кнопочник «Ом» в положение 1.

·  Установить на магазине емкостей кнопочник мкФ в положение «1»? кнопочник множителя в положение 10^-3.

·  Включить в сеть стойку, генератор, осциллограф.

·  Снять резонансную кривую контура для частоты 14 кГц при С=1` 10^-3 мкФ и сопротивлениях контура 1, 100, 1000 Ом. Для этого, вращая ручку частоты от 10 кГц до 18 кГц на генераторе через 1 кГц заносить в таблицу величину сигнала на осциллографе.

C= 110-3 мкФ
R=1 Ом			R=100 Ом			R=1000 Ом
f,кГц	U, дел		f,кГц	U, дел		f,кГц	U, дел

·  Определить индуктивность контура. При резонансе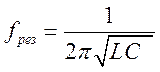 , тогда

L=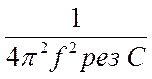

·  Определить полосу пропускания контура по резонансной кривой  --частоты на уровне 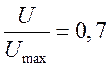, по разные стороны от максимума резонансной кривой.

Контрольные вопросы

1.  Что такое идеальный колебательный контур?

2.  Формула Томсона.

3.  Чем отличается реальный контур от идеального?

4.  Начертить схему контура для наблюдения вынужденных колебаний.

5.  Что такое резонанс?

6.  Дифференциальное уравнение вынужденных колебаний.

7.  Условия наблюдения резонанса в контуре.

8.  От чего зависит острота пика резонансной кривой? Проанализируйте полученные резонансные кривые.

9.  Что такое полоса пропускания контура?

10.  Где используются колебательный контур?

Литература

1.Г.А. Зисман, О.М. Тодес. Курс общей физики, т.II, 51

2. С.Э. Фриш, А.В. Тиморова. Курс общей физики, т.II, 239-240.