Изучение заряда и разряда конденсатора

Лабораторная работа № 60

Изучение заряда и разряда конденсатора

Цель работы: изучение закономерностей заряда и разряда конденсатора в электрической цепи и определение постоянной времени разряда.

Приборы: генератор электрических импульсов, магазин сопротивлений и емкостей, осциллограф.

Введение

Электрическое оборудование, различные электронные приборы и аппараты стали неотъемлемой частью нашей жизни. Их устройство весьма разнообразно, однако все они реализованы на основе ряда простейших электрических элементов, соединенных в электрические цепи. Важнейшими из этих элементов являются резисторы или сопротивления, индуктивности, конденсаторы или емкости.

Хорошо известно, что при заряде проводника, его поверхность является эквипотенциальной, что дает право говорить о потенциале проводника, подразумевая потенциал любой его точки.

Для получения одного и того же потенциала различным проводникам требуется сообщить разные заряды. С этой точки зрения любое уединенное проводящее тело характеризуется емкостью.

Электрическая емкость C определяется как заряд q, который нужно сообщить проводнику, чтобы его потенциал j (относительно бесконечности) стал равен единице:

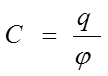                                                                   (1)

Емкость проводника не зависит ни от заряда, ни от потенциала, равно, как, например, емкость чайника или кастрюли не определяется чем и на сколько они заполнены. Величина C связана только с размерами и формой проводника, присутствием других проводящих тел и диэлектрическими свойствами окружающей среды.

Единица измерения емкости фарад (Ф) имеет размерность кулон/вольт. Фарад - очень большая величина. Так, например, емкость в 1Ф обладал бы уединенный шар с радиусом 9·10⁹ м, который в 1,5 тыс. раз превышает радиус Земли.

Уединенный проводник как правило обладает небольшой емкостью. Даже шар таких размеров как Земля имеет емкость порядка 700 мкФ. Вместе с тем на практике часто требуются устройства, которые при небольшом потенциале накапливали бы на себе (конденсировали) значительные заряды. В основу таких устройств – конденсаторов положен факт возрастания емкости проводника при приближении к нему других тел. Это происходит за счет уменьшения потенциала проводника (см. (1)).

Конденсатор представляет собой два близко расположенных проводника, называемых обкладками. Его емкость определяется выражением

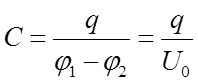
                                                                      (2)

где q – заряд на обкладках, U₀=j₁-j₂ – потенциал между обкладками или напряжение на конденсаторе.

Для изучения закономерностей заряда и разряда конденсатора рассмотрим электрическую цепь, представленную на рис. 1.

                 R                     C                       R                     C 

 

                                  -q  +q                                       -q +q

                                          2                                                             2

                                                                                         П

                          П          1             e                                     1       e 

                                        а)                                                 б)

Рис.1

Здесь последовательно соединенные конденсатор с емкостью C и сопротивление R с помощью переключателя П могут подключаться к источнику ЭДС, величина которой e . Этот источник осуществляет заряд конденсатора, если переключатель находится в положении “1” (рис.1а.). Если переключатель стоит в положении “2” (рис.1б.), то предварительно заряженный конденсатор разряжается через сопротивление R.

Пусть в результате заряд конденсатора его обкладкам сообщен заряд q и –q. Поместим переключатель П в положение “2” (рис.1б.), предоставив конденсатору возможность разрядиться. Заряд под действием созданной разности потенциалов U_c=qc^-1 сразу начнет перетекать с одной обкладки на другую, образуя в цепи электрический ток. Это движение прекратится как только на обкладках заряды будут скомпенсированы. Процесс перехода зарядов с одной на другую (или разряд) не происходит мгновенно. Его длительность определяется характеристиками цепи, т.е. величинами R и C.

Действительно, проходя по электрической цепи, заряды испытывают сопротивление. Чем больше R (например R®¥, что в пределе отвечает разомкнутой цепи), тем больше требуется времени (в пределе вечность) для разряда конденсатора. Если при прочих равных условиях емкость велика, а это значит, что на обкладках накоплен большой заряд, то для его перетекания с одной обкладки на другую требуется значительное время.

Для количественного описания процесса заряда и разряда в цепи, представленной на рис.1, воспользуемся правилами Кирхгофа. Эти правила позволяют рассчитать любые самые сложные электрические цепи. Их содержание составляют следующие утверждения:

1. Сумма токов, входящих в узел, равна сумме токов, выходящих из узла. При этом узлом называют соединение не менее трех проводников.

2. При обходе вдоль выделенного замкнутого электрического контура алгебраическая сумма падений напряжений на каждом элементе цепи равна алгебраической сумме ЭДС, включенных в этом контуре:

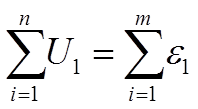
Здесь величина напряжения U₁ (ЭДС e₁) считается положительной, если выбранное направление обхода контура и направление электрического тока в нем (направление действия ЭДС) совпадают. Заметим, что направление действия ЭДС принято обратным направлению электрического поля в источнике.

Так, применяя правила Кирхгофа к электрической цепи рис.1, найдем

                          U_R+U_C=0, U_R=I·R, U_C=q·C^-1                    (3)

где через I обозначена сила тока в этой цепи. Учитывая, что 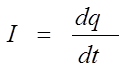из (3) следует уравнение для заряда

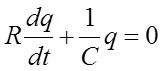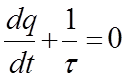                         или        ,               (4)

где введенная величина называется постоянной времени для RC цепи. Она определяет временные характеристики процесса разряда.

Уравнение (4) описывает изменение заряда на обкладках конденсатора с течением времени. Пусть в начальный момент времени t=0 на обкладках был заряд

                                              q(0)=q₀                                            (5)

С учетом начального условия (5) решение (4) имеет вид

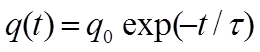                                                                    (6)

С помощью (6) для величины тока в цепи 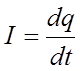 и напряжения на конденсаторе 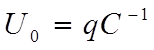 найдем

                                                                   (7)

                                   

Видно, что при разряде конденсатора заряд, ток и напряжение на нем спадают от своего первоначального значения до нуля. Постоянная  

определяет характерный временной масштаб процесса разряда: чем больше величина (напоминает, что ), тем медленнее происходит разряд. При электрические величины (6) и (7) уменьшаются в  раза по сравнению с первоначальным значением.

Применение правила Кирхгофа для схемы на рис.1а позволяет проанализировать процессы заряда конденсатора. Так, учитывая, что в контур включена ЭДС вместо первого равенства в (3) будет уравнение 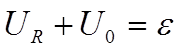, тогда (ср. с (4)).

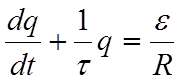
Решение этого уравнения с начальным условием q(o)=0 (в начальный момент времени конденсатор не заряжен) имеет вид

а для напряжения на конденсаторе следует выражение

где 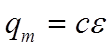 и 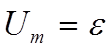 заряд и напряжение на конденсаторе, возникающее после его заряда. Как и в случае разряда постоянная характеризует время нарастания заряда и напряжения. Для определения удобно использовать систему координат, где экспоненциальные зависимости напряжения типа (7) принимают вид прямой. Так, обозначая