ПРИМЕРЫ ВОПРОСОВ И
ЗАДАЧ ПО ЛИНЕЙНОЙ АЛГЕБРЕ, КОТОРЫЕ МОГУТ БЫТЬ НА ЭКЗАМЕНЕ
(2007)
/Тема «Матрицы и определители»/
- Даны матрицы А, В. Найти АВ и ВА, если соответствующие
произведения имеют смысл.
- Даны матрицы А, В. Найти А2-2В+3Е.
- Дана квадратная матрица А. Найти АТ-2Е.
- Привести пример квадратной матрицы А третьего порядка,
отличной от единичной. Найти АТ.
- Дана квадратная матрица 3-го порядка. Вычислить ее
определитель.
- Дана квадратная матрица 3-го порядка. Вычислить ее
определитель любым способом, кроме правила треугольников.
- Дана квадратная матрица 3-го порядка. Вычислить ее
определитель разложением по заданной строке (столбцу).
- Дана квадратная матрица 3-го порядка. Найти
алгебраическое дополнение элемента, стоящего в третьей строке и во втором
столбце.
- Привести пример невырожденной матрицы 2-го порядка.
- Привести пример вырожденной матрицы.
- Дана квадратная матрица 3-го порядка. Является ли она
а) вырожденной?
б) симметричной?
- Дана квадратная матрица А 3-го порядка. Найти обратную
матрицу.
- Даны квадратные матрицы А и В (2-го или 3-го порядка). Не
вычисляя А-1 , проверить, является ли матрица В обратной для
матрицы А.
- Дана квадратная матрица А (2-го или 3-го порядка).
Выяснить, существует ли для нее обратная матрица.
/Тема «Системы линейных уравнений»/
- Привести пример ступенчатой системы линейных уравнений.
Записать расширенную матрицу этой системы.
- Решить систему линейных уравнений методом Крамера
(количество уравнений и неизвестных либо 2, либо 3).
- Решить систему линейных уравнений с тремя неизвестными
методом Гаусса (количество уравнений 2-4).
- Привести
пример однородной системы линейных уравнений с симметричной матрицей
коэффициентов.
- Привести пример несовместной системы линейных уравнений.
/Тема «Векторы»/
- Даны векторы А=(-2; 1; 4; -1), В=(3; 0; 2; 1). Найти длины
этих векторов и скалярное произведение
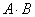 .
.
- Даны векторы А=(-2; 1; 4; -1), В=(3; 0; 2; 1). Найти их
сумму (разность) и скалярное произведение.
- Известно, что длина вектора А равна 2, длина вектора В
равна 1, а скалярное произведение этих векторов
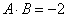 . Найти скалярное произведение
. Найти скалярное произведение
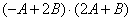 .
.
- Являются ли
векторы А=(1;-2;0;-1) и В=(0;2;3;-4) ортогональными?
- Привести пример линейно зависимого набора из трех векторов
в R3 .
- Привести пример линейно независимого набора из двух
векторов в R4.
- Являются ли линейно независимыми следующие наборы
векторов:
а)  ,
, 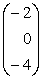 ,
,
 ; б)
; б) 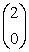 ,
,
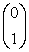 ,
, 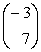 ?
?
27. Является ли линейно
зависимым набор векторов
Х1=(-1; 1), Х2=(1;
0), Х3=(21; 13)?
- Привести пример линейно зависимого набора из 2-х векторов
в R3.
- Привести пример линейно зависимого набора векторов в R2.
- Привести пример линейно независимого набора векторов в R2.
- Изобразить графически какой-либо линейно независимый набор
векторов в R2.
- Изобразить графически какой-либо линейно зависимый набор
векторов в R2.
- Найти собственные значения матрицы
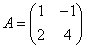 .
.
- Записать матрицу квадратичной формы
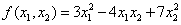 .
.
![]() .
.![]() ,
, ![]() ,
,
![]() ; б)
; б) ![]() ,
,
![]() ,
, ![]() ?
?