Розв’язування систем лінійних рівнянь з двома змінними способом додавання: План-конспект уроку алгебри

План-конспект уроку

Тема:розв’язування систем лінійних рівнянь з двома змінними способом додавання.

Тип уроку:урок засвоєння нових знань.

Мета уроку:

навчальна: навчити учнів розв’язувати системи рівнянь з двома змінними способом додавання, вибирати найбільш раціональний спосіб розв’язання даної системи;

розвиваюча: розвивати логічне мислення;

виховна:      виховувати графічну культуру, уважність.

План

1.  Організаційний момент ( 2 хвилини );

2.  Перевірка домашнього завдання (5 хвилин );

3.  Актуалізація опорних знань ( 10 хвилин );

4.  Виклад нового матеріалу ( 15 хвилин );

5.  Закріплення нового матеріалу ( 9 хвилин );

6.  Підсумки уроку ( 2 хвилини );

7.  Домашнє завдання ( 2 хвилини ).

Хід уроку

1.  Організаційний момент.

Вчитель оголошує план даного уроку:

1)  самостійна робота;

2)  виклад нового матеріалу;

3)  закріплення нового матеріалу.

2.  Перевірка домашнього завдання (самостійна робота ).

Клас поділяється на два варіанти. Учні розв’язують системи на листочках, після чого здають їх вчителеві на перевірку.

Перший варіант.

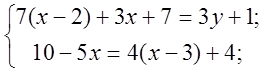
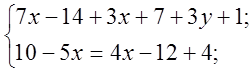
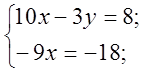
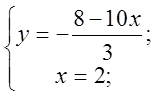
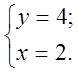
Другий варіант.

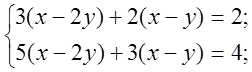
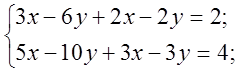
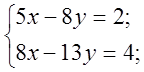
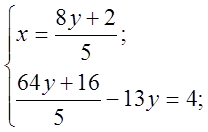
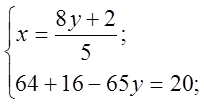
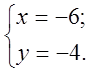
3.  Актуалізацію опорних знань вчитель проводить у формі фронтального опитування.

Питання:

1)  Чим є графік лінійного рівняння з двома змінними?

2)  Що означає розв’язати систему рівнянь з двома змінними?

3)  Скільки розв’язків може мати система двох лінійних рівнянь з двома змінними?

4)  Як розв’язують систему двох лінійних рівнянь з двома змінними графічним способом?

5)  Як розв’язують систему двох лінійних рівнянь з двома змінними способом підстановки?

4.  Виклад нового матеріалу.

Вчитель пояснює новий матеріал.

Отже ви вже знаєте два способи розв’язування систем двох лінійних рівнянь з двома невідомими. Це графічний спосіб і спосіб підстановки. Але є ще один спосіб - спосіб додавання. Ми розглянемо його на сьогоднішньому уроці.

Розглянемо ту ж систему, що й на минулому уроці.

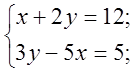    (1)

Домножимо перше рівняння системи на 5

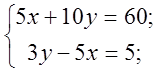
Додамо почленно ліві й праві частини рівнянь. Дістанемо рівняння з одним невідомим:

13y=65

Замінимо яке не будь з рівнянь системи (1) (наприклад друге) отриманим рівнянням.

        (2)

Розв’яжемо цю систему. З другого рівняння знаходимо:

y=5;

Підставивши це значення у перше рівняння, отримаємо:

x+25=12;

x+10=12;

x=2.

Пара чисел (2;5) є розв’язком системи (2). Вони ж будуть розв’язком системи (1).

Зробимо перевірку:

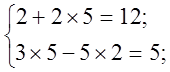
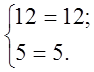
Отже можемо зробити висновок, що системи (1) і (2) рівносильні.

На минулому уроці при розв’язуванні цієї системи графічним способом і способом підстановки ми дістали той же розв’язок. Отже бачимо, що розв’язок не залежить від вибору способу розв’язування.

5.  Закріплення нового матеріалу.

Один учень розв’язує приклад біля дошки, інші в зошитах.

1)

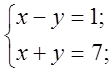
2)

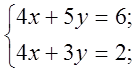
3)

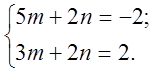
6.  Підсумки уроку.

Учитель запитує у декількох учнів про особливості застосування способу додавання про розв’язуванні системи двох лінійних рівнянь з двома змінними.

7.  Домашнє завдання.

§6,п.5,

№№ 842,843(а).