



Файл Самостоят_05.doc 4 стр. 146 Кбайт.
1. Программирование дифференциальных уравнений в частных производных.
В данном разделе мы ограничимся рассмотрением методов решений дифференциальных уравнений в частных производных на примере линейных дифференциальных уравнений вида
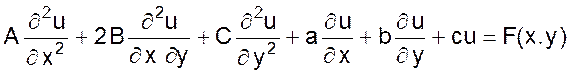 (01)
(01)
где A, B, C, a, b, c – заданные коэффициенты, которые могут быть постоянными или функциями аргументов x, y;
F(x, y) – заданная функция переменных x и y.
Решение u(x, y) должно удовлетворять уравнению 01 в некоторой области переменных x и y, граница которой задается уравнением Г(x, y) = 0.
В зависимости от знака дискриминанта D = AC – B2 уравнение 01 можно отнести к одному из типов: эллиптическому (D > 0), параболическому (D = 0), гиперболическому (D < 0), смешанному, когда D не сохраняет знак в заданной области, ограниченной кривой Г(x, y) = 0.
К наиболее известным уравнениям первого типа относится уравнение Пуассона
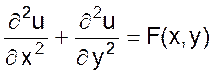 (02)
(02)
и его частный случай уравнение Лапласа
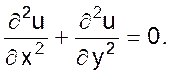 (03)
(03)
В частности, уравнение 02 описывает стационарные процессы, связанные с распределением температуры в пластине.
К уравнениям параболического типа относится уравнение теплопроводности, (диффузии)
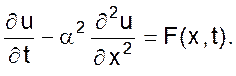 (04)
(04)
Данное уравнение описывает нестационарное распределение температуры вдоль тонкого однородного стержня. Решение u(x, t) представляет собой температуру сечения стержня с координатой x в момент времени t.
Примером уравнения гиперболического типа может служить волновое уравнение
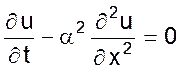 , (05)
, (05)
которое описывает свободные колебания струны.
Решение u(x, t) физически представляет собой поперечное перемещение струны в сечении x для момента времени t.
Естественно положить, что для уравнений, описывающих нестационарные физические процессы, то есть такие, которые протекают и во времени, и в пространстве, решение u(x, t) должно удовлетворять уравнению как при определенных значениях переменных, относящихся к начальному моменту времени (начальные условия), так и относящихся к фиксированным значениям пространственных координат (краевым условиям).
При решении уравнений в частных производных встречаются три типа краевых задач.
Задача Дирихле.
Решение u(x, y) уравнения 01 на границе области должно совпадать с некоторой наперед заданной функцией φ(x, y), то есть uГ(x, y) = φ(x, y).
Задача Неймана.
Решение u(x, y) уравнения 01 должно быть таким, чтобы его нормальная производная ¶u/¶n совпадала бы на границе области Г(x, y) с некоторой, наперед заданной функцией φ(x, y), то есть (¶u/¶n)Г = φ(x, y). Кроме того, решение должно принять некоторое заданное значение m в некоторой заданной точке x*,y* области, то есть u(x*,y*) = m.
Третья краевая задача.
Задача смешанного типа, когда на границе области Г(x, y) = 0 задается линейная комбинация значений функции u(x, y) и ее нормальной производной a (¶u/¶n)Г + b uГ(x, y) = φ(x, y).
С учетом изложенного, например, решение уравнения теплопроводности 04 применительно к стержню длины L может отыскиваться для таких условий:
u(x, 0) = φ(x) (распределение температуры вдоль стержня для момента времени t = 0);
краевых условий u(0, t) = φ1(t) (температура левого конца стержня меняется во времени как φ1(t)) и u(L, t) = φ2(t) (для правого конца стержня).
Решение уравнений в частных производных можно воспроизвести приближенно, путем решений систем обыкновенных дифференциальных уравнений, аппроксимирующих исходные уравнения. Эта методика получила название «метод прямых».
Пример 6.
Пусть требуется найти распределение температур по глубине стенки, которая разделяет две среды с разной температурой: слева – среда, температура которой меняется во времени как φ1(t), а справа – как φ2(t). Толщина стенки L.
Введем переменные, с помощью которых описывается распределение температуры по глубине стенки. С этой целью перпендикулярно стенке проведем ось y. Тогда температура внутренних точек стенки – функция двух переменных: координаты y и времени t, то есть u (y, t).
Точки стенки, лежащие на одной вертикали, имеют одинаковую температуру, вследствие большой площади стенки и ее однородности.
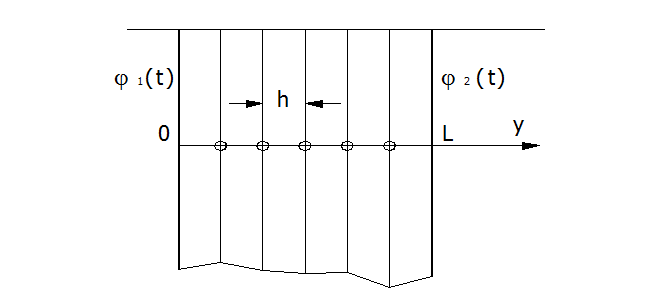
Рис. П6.1. Схема исследуемого объекта.
Функции u(y, t) удовлетворяет уравнение теплопроводности
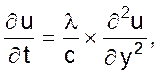 (06)
(06)
где l - коэффициент теплопроводности,
c – удельная объемная теплоемкость стенки.
Решение уравнения 06 должно соответствовать краевым условиям:
u(0, t) = φ1(t),
u(l, t) = φ2(t)
и начальному условию
u(y, 0) = T(y).
Здесь T(y) – некоторая заданная функция, характеризующая распределение температуры по толщине стенки в первоначальный момент времени.
Заменим уравнение теплопроводности системой обыкновенных дифференциальных уравнений, для чего мысленно разобьем стенку вертикальными линиями на ряд (n) слоев одинаковой толщины h. При пересечении прямых с осью y образуется ряд точек, температуру в которых можно рассматривать функцией одной переменной - времени. Теперь частная производная (сомножитель правой части уравнения 06) может быть выражена приближенно через значения функции u(y, t) в точке yj и в двух соседних с ней точках j + 1 и j – 1 формулой
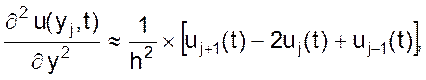 (07)
(07)
где uj+1(t) = u(yj+1, t); uj-1(t) = u(yj-1, t).
Или, обозначив uj(0) = T(yj) = Tj; m = l / ch2; u(0, t) = u0(t) = φ1(t); un+1(t) = φ2(t), уравнение 06 для отдельной j-й точки запишем в виде
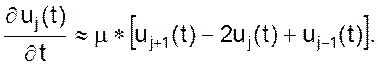 (08)
(08)
Естественно, для аппроксимации функции 06 в целом нам понадобится система из n обыкновенных дифференциальных уравнений первого порядка.
Представим и решим систему обыкновенных дифференциальных уравнений средствами SIMULINK. Начнем с решения дифференциального уравнения 1 порядка.
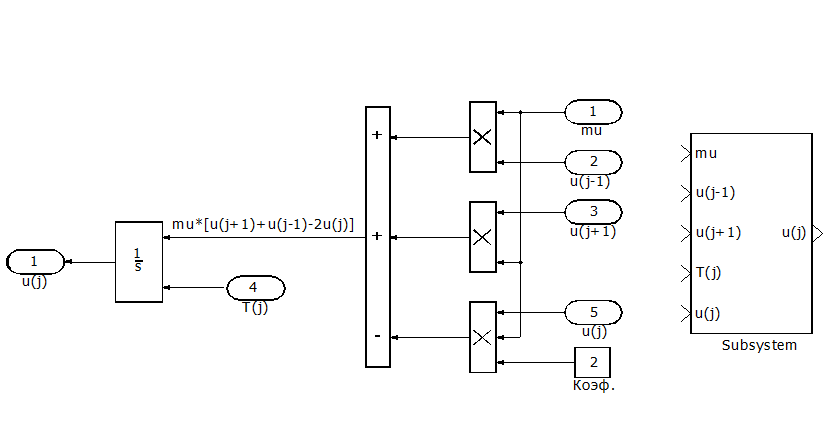
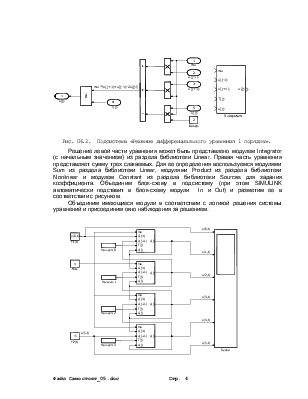
Рис. П6.2. Подсистема «Решение дифференциального уравнения 1 порядка».
Решение левой части уравнения может быть представлено модулем Integrator (с начальным значением) из раздела библиотеки Linear. Правая часть уравнения представляет сумму трех слагаемых. Для ее определения воспользуемся модулями Sum из раздела библиотеки Linear, модулями Product из раздела библиотеки Nonlinear и модулем Constant из раздела библиотеки Sources для задания коэффициента. Объединим блок-схему в подсистему (при этом SIMULINK автоматически подставит в блок-схему модули In и Out) и разметим ее в соответствии с рисунком.
Объединим имеющиеся модули в соответствии с логикой решения системы уравнений и присоединим окно наблюдения за решением.
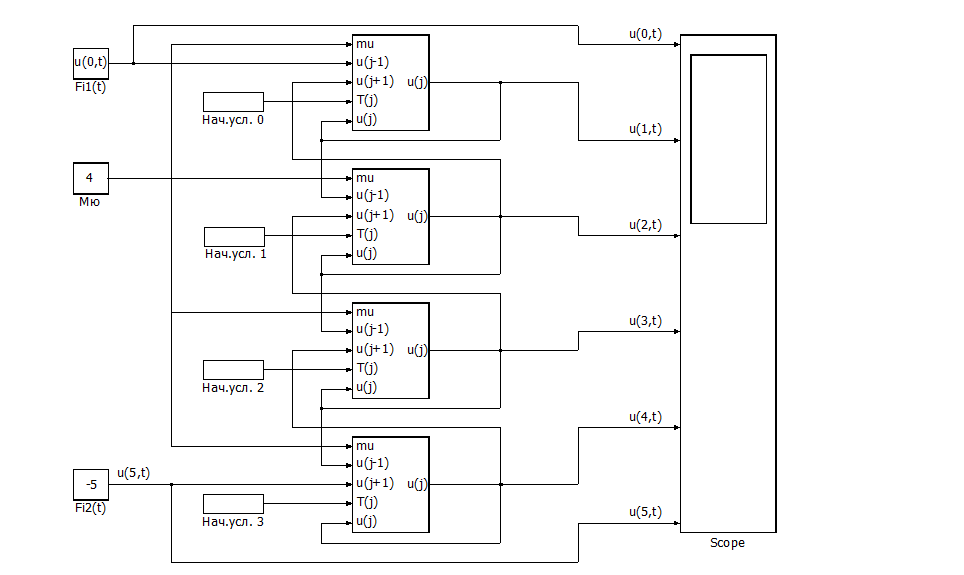
Рис. П6.3. Блок-схема решения задачи[1].
Теперь остается задать начальные условия, значение Мю и функции изменения температуры разделяемых стенкой сред. После чего можно запустить задачу на решение и, получив его, проанализировать.
[1] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_05 p6ris3»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.