Обработка результатов измерения и выбор термопреобразователя, страница 3

При проверки статической независимости данных используем критерий отношений квадратов последовательных разностей, т.е. для соседних элементов выборки Х_i  и X_i+1 рассчитываем статистику:

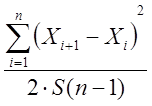,                                                  (2.47)

и сравниваем со значением:

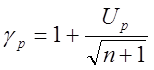,                                                 (2.48)

где     U_p – квантиль нормированного нормального распределения. Если выпол-

          няется условие: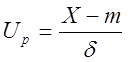

Если выполняется неравенство:

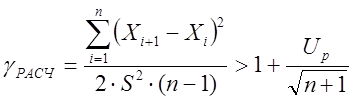,                                   (2.49)         

то гипотеза о независимости элементов выборки применяется с заданной (доверительной) вероятностью (99%).

 Проверку нормальности проводят для выборок с коэффициентом вариации не более 33%. В работе проводим два метода проверки: по среднему абсолютному отклонению (САО) и по оценкам параметров форм распределения (асимметрии, эксцесса).

Для выборки, имеющей приближенно нормальное распределение, должно выполняться неравенство:

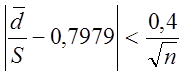,                                               (2.50)

где  САО d определяется по формуле:

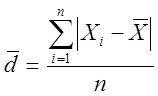,                                                 (2.51)

Условием нормальности распределения по второму методу является выполнение неравенств:

,                                                 (2.52)

,

где      S_ан и S_ен – среднее квадратичное отклонение показателей асимметрии и

            эксцесса:

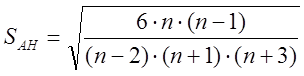,                                       (2.53)

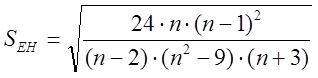.                                      (2.54)

Для проверки однородности нескольких дисперсий при равных объемах всех рассматриваемых выборок будем использовать G – критерий Кохрена. Который вычисляем по формуле:

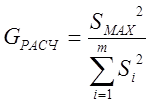,                                                    (2.55)

где       m – количество выборочных дисперсий, однородность которых прверя-

            ется;

            S₁², S₂²,…S_m² – выборочные дисперсии, которые берутся из предвари          

            тельной статической обработки.

Число степеней свободы находим по формуле:

.                                                     (2.56)

где       п – количество измерений для одной выборки.

По уровню значимости и количеству степеней свободы находим табличное значение коэффициента Кохрена. Если выполняется условие G_расч < G_таб , то гипотеза об однородности дисперсий принимается.

Принимаем S₁=0,0132; S₂=0,0387; S₃=0,055; и подставляем их  в формулу (2.55), получаем:

.

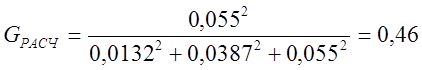В каждой выборке (одинакового объема) содержится по  экспериментальных данных. Исходя из этого, число степеней свободы находим по формуле (2.56).

,

Уровень значимости для расчетов принят 0,01. По этим данным из [  ] находим табличное значение коэффициента Кохрена для наших данных G_таб=0,52. Так как условие G_расч < G_таб выполняется (0,46 < 0,52), то гипотеза об однородности дисперсий принимается.

2.5.2 Регрессионный анализ и построение полиномиальной модели,

описывающей номинальную статистическую характеристику

преобразователя  

Расчет ведем методом наименьших квадратов

,                                  (2.57)

где       m – степень полинома.

Расчет начинается со степени 1, затем производим проверку адекватности полиномиальной модели по формуле:

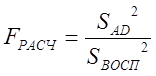,                                                 (2.58)

где      S_ay² – адекватность;

            S_восп² – воспроизводимость.

Для  того чтобы уравнение полиномиальной модели было адекватно, необходимо чтобы выполнялось неравенство:

,                                                   (59)

где       F_табл – табличное значение коэффициента Фишера.

то уравнение полиномиальной адекватно.

В нашем случае полином описывается уравнением со степенью 1.

Коэффициенты полинома: С(0) = 9,998; С(1) = 0,0426.

Критерий Фишера: S_ВОС = 0,00129; S_АД = 0,000001; F₁ = 1; F₂ =15. Подставляем эти данные в формулу (2.58), получаем:

,

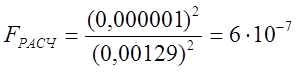Из [  ] находим табличное значение F – критерия Фишера. F_табл = 8,69. Из расчета видно, что условие (2.59) выполняется, т.е. 8,69 > 2,06*10^-5 , следовательно уравнение адекватно.

Результат расчета полиномиальной модели второго порядка приведен в таблице .

Таблица    - Результаты расчета полиномиальной модели

Х[1]=50	12,13217	12,13274	0,00062
Х[2]=100	14,268	14,268	0,00125
Х[3]=150	16,4	16,40085	0,00062

По данным таблицы строим график полиномиального анализа (лист АПП.00000 .052 ). Затем с помощью него подбираем термопреобразователь.

Для выбора термопреобразователя необходимо определить погрешность. Для этого используем таблицу

Таблица     - Арифметическая погрешность термопреобразователя 

Х[1-5]	Y[1-5]	Y[1-4]	Y[1-4]-Y[1-4]табл
50	12,13217	12,14	0,00783
100	14,268	14,208	0,06
150	16,4	16,419	0,019

 Расчет проводим для наибольшего отклонения по формуле:

,                                                 (60)

где  t – измеряемая температура в ⁰С.

Принимаем t=150 ⁰С и подставляем в формулу (60 ), получаем:

В результате проделанной работы, произведена обработка результатов измерения, которая включает в себя: статистическую обработку выборочных данных, проверка гипотез по ним на предмет нормальности распределения данных выборках, однородности дисперсий, независимости данных; определение коэффициентов полиномиальной модели и проверки её адекватности по экспериментальным данным. Результатом расчета является выбор термопреобразователя (ТСМ 10М) по графику функциональной зависимости (лист АПП.000003.052 РР). Сравнив теоретическое значение с максимальным отклонением из таблицы [  ] (0,775>     )делаем вывод, что допустимое отклонение преобразователя находится в пределах нормы и что прибор пригоден к эксплуатации.