В результате расчета максимальный расход Qmax получился меньше предельного Qпр (100 > 99), следовательно расчет выполнен правильно.
Результатом расчета является выбор стандартного сужающего устройства (ДКС 0,6 - 50) в соответствии с технологическими параметрами.
Метрологическое исследование проводим с тем, чтобы правильно подобрать термопреобразователь, который должен обеспечивать точность измерения диапазоне измерений. В противном случае измерения будут проходить с большой погрешностью. Состоит метрологическое исследование из статистической обработки и регрессионного анализа.
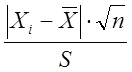 (2.34)
(2.34)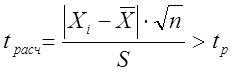 (2.35)
(2.35)где tp – значение коэффициента Стьюдента при заданной доверительной
вероятности Р и числе степеней свободы f = n-1;
S – среднее квадратическое отклонение.
Если неравенство не выполняется, то проверяемый по tp – критерию элемент сохраняется в выборке. Выборка, оставшаяся после исключения аномальных результатов приведена в таблице
|
Х, 0С |
50 |
100 |
150 |
|
1 |
2 |
3 |
4 |
|
Y, Ом |
12,136 |
14,236 |
16,35 |
|
12,128 |
14,3 |
16,45 |
|
|
12,132 |
14,236 |
16,35 |
|
|
12,129 |
14,268 |
16,35 |
|
|
12,136 |
14,268 |
16,44 |
|
|
12,128 |
14,3 |
16,44 |
Статическая характеристика: теоретические распределения случайной величины описываются функциями распределения и числами – характеристиками или параметрами распределения. Эмпирические распределения (выборки) могут быть описаны гистограммами, полигонами, кумулятами и числами – выборочными характеристиками или оценками параметров. Задачей предварительной статистической обработки является оценивание неизвестных параметров. Оценка параметров (выборочная характеристика) представляет собой функцию от полученных значений случайной величины и может быть точечной или интервальной. Точечная оценка – оценка параметров распределения одним числом.
Для исследовании результатов эксперимента рассчитаем следующие характеристики:
- выборочное среднее арифметическое (оценка математического
ожидания):
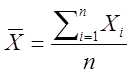 ,
(2.36)
,
(2.36)
- выборочное среднее квадратичное отклонение (несмещенная оценка
дисперсии):
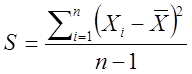 ,
(2.37)
,
(2.37)
- выборочные центральные моменты (оценка моментов) первых четырех
порядков К=(1 - 4):
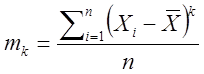 ,
(2.38)
,
(2.38)
- выборочное значение (оценка коэффициента вариации):
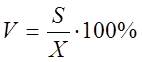 ,
(2.39)
,
(2.39)
- размах выборки
![]() ,
(2.40)
,
(2.40)
- среднее арифметическое среднего квадратического отклонения:
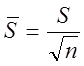 ,
(2.41)
,
(2.41)
Перечисление оценки характеризуют положение, разброс, относительную изменчивость выборки.
Рассчитываются также выборочные характеристики формы распределения, позволяющие проверить гипотезу о нормально распределенных числах:
- показать асимметрии:
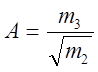 ,
(2.42)
,
(2.42)
и его несмещенная оценка:
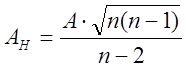 ,
(2.43)
,
(2.43)
- показатель эксцесса:
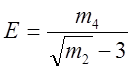 ,
(2.44)
,
(2.44)
и его несмещенная оценка:
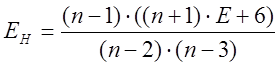 ,
(2.45)
,
(2.45)
Вычисляемые по приведенным формулам оценки в большинстве удовлетворяют основным требованиям качества: состоятельности – сходимости к оцениваемому параметру при неограниченном объеме эксперимента; несмещенности – совпадении математического ожидания и истинным значением; эффективности – наименьшего разброса оценки относительно истинного значения по сравнению с другими оценками.
Точечная оценка не является полной, так как указывает только на границы интервала, но не вероятность попадания в интервал истинного значения. Более полной является интервальная оценка – интервал, включающий в себя значение оцениваемого параметра с заданной (доверительной вероятностью). Для нормально распределенных чисел оценка математического ожидания (истинного значения) при неизвестной дисперсии d2 определяется неравенством:
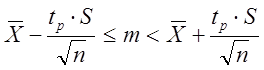 ,
(2.46)
,
(2.46)
В работе определяем интервальную оценку для Р = 99%. Результат статической обработки выборок приведен в таблице
Таблица - Результаты статистической обработки выборок
|
Температура, 0С |
50 |
100 |
150 |
|
12,132 |
14,268 |
16,4 |
|
|
Среднее квадратическое отклонение |
0,0137 |
0,03871 |
0,055 |
|
Среднее абсолютное отклонение |
0,00256 |
0,02142 |
0,0502 |
|
Коэффициент вариации, % |
0,02779 |
0,2012 |
0,33548 |
|
Показатель асимметрии |
0,04891 |
0,00369 |
0 |
|
Показатель эксцесса |
-3 |
-2,99999 |
-2,9998 |
|
Нижняя граница доверительного интервала |
12,1266 |
14,221 |
16,309 |
|
Верхняя граница доверительного интервала |
12,1377 |
14,3154 |
16,4909 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.