Изучение и составление математической модели ресивера

Содержание

Введение………………………………………………………………………………………...     3

1. Математическая модель ресивера………………………………………………………….     4

2. Программа и методика проведения измерений……………………………………………9

2.1. Описание лабораторной установки…………………………………………………...     9

2.2. Определение диапазонов изменения величин………………………………………..     9

2.3. Определение времени переходного процесса………………………………………..10

2.4. Определение зоны регулирования…………………………………………………….11

Заключение…………………………………………………………………………………..11

Используемая литература ..………………………………………………………………...12

Введение

Проектирование автоматических систем управления и регулирования, их работа  напрямую зависит от того, насколько точно составлены математические модели управляемых объектов.

Нередко инженеру самому приходится составлять аналитические математические или физические модели для объектов управления.

Целью данной курсовой работы является изучение и составление математической модели ресивера.

1.  МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РЕСИВЕРА

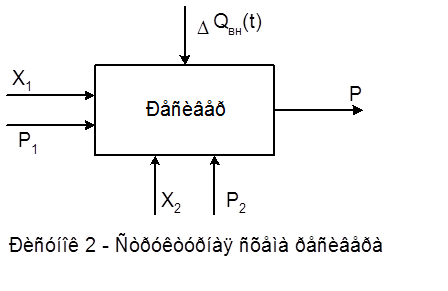
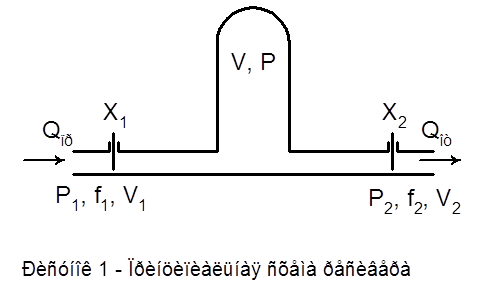На рисунке 1 представлена принципиальная схема ресивера. Ресивер представляет собой металлический баллон, с подсоединенными патрубками подвода и отвода воздуха. На входе и выходе патрубков находятся регулирующие расход и давление воздуха органы X₁ и X₂.

Примем, что проходные сечения f₁ и f₂ зависят только от положений регулирующих органов X₁ и X₂ соответственно, и пропорциональны им.

Приток воздуха в ресивер обеспечивается подпором P₁, а отток воздуха в среду (или атмосферу) происходит с постоянным противодавлением P₂.

В установившемся состоянии давление газа в ресивере постоянно, P = P_o = const, что обеспечивается равенством приходящего и отходящего расходов воздуха, O_пр и Q_от соответственно.

Уравнение баланса, установившегося состояния имеет вид:

Q_пр0 = Q_от0;                                                                                                                      (1)

Нарушение данного условия приводит к возникновению динамических процессов  в ресивере. Разность приходящего и отходящего расхода определяет количество воздуха, накапливающегося в ресивере в единицу времени.

Уравнение динамики процесса имеет вид:

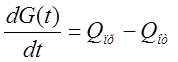,                                                                                                          (2)

где G = V · g - количество воздуха c удельным весом g, в объеме V.

Распишем расходы Q_пр и Q_от:

Q_пр = Q_пр0 + DQ_пр;

Q_от = Q_от0 + DQ_от.

Т.к. объем ресивера постоянен, то имеем право записать:

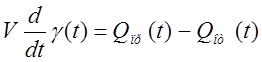                                                                                             (3)

Учитывая неизбежные внешние возмущения, системы запишем:

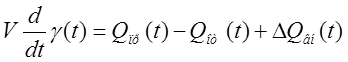
Будем считать закон истечения газов адиабатным, и обозначим давления воздуха на входе в ресивер через P_x, а на выходе P_у.

Для докритического истечения газа:

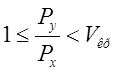,   где 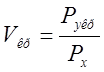 .    Учитывая вышесказанное, распишем Q_пр и Q_от:

,

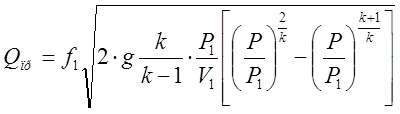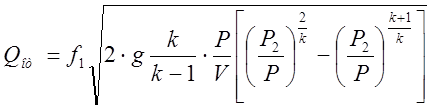, где

f₁, f₂ – эффективные площади проходных сечений входа и выхода соответственно;

g – ускорение свободного падения;

k – показатель адиабаты;

V – удельный объем газа.

Поскольку связи между P1 и V1, а также между P и V однозначно определены и выражаются уравнениями адиабатического процесса, можно утверждать что функции расходов Q_пр и Q_от зависят только от X₁, P₁, P и  X₂, P, P₂ соответственно. Запишем:

Q_пр = Q_пр(X₁, P₁, P);

Q_от = Q_от(X₂, P, P₂).                                                                                                         (4)

Для надкритического истечения газа:

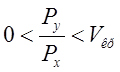
Расходы притока и оттока воздуха определяются соответственно соотношениями:

,

.

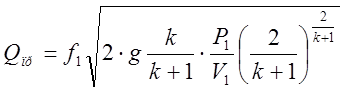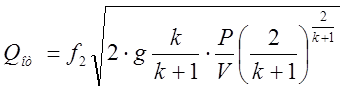В этом случае имеем зависимости:

Q_пр = Q_пр(X₁, P₁);

Q_от = Q_от(X₂, P₂).                                                                                                             (5)

т.е. расходы в надкритическом истечении газа не зависят от давления в самом ресивере P.

В последующих рассуждениях будем учитывать только докритическое истечение газов. Структурная схема ресивера, для нашего случая представлена на рисунке 2.

Разложим зависимости (4) в ряды Тейлора и линеаризуем их. После преобразований имеем:

,

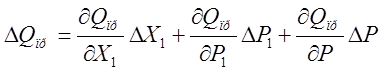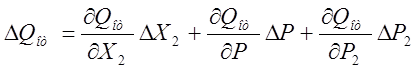.                                                                   (6)

Для адиабатического процесса связь давления воздуха в ресивере с его удельным весом выражается уравнением:

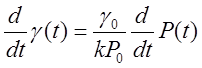,                                                                                                      (7)

где g_o и P_o начальные (установившиеся) значения удельного веса и давления воздуха в ресивере соответственно.

На основании балансового уравнения (3), и вышеизложенного (7), объединив левую и правую части уравнений (6), получим:

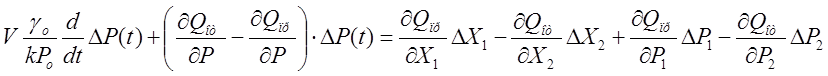,        (8)

Левая часть уравнения представляет собой собственный оператор системы, выражение в скобках представляет собой значение фактора устойчивости системы:

, 

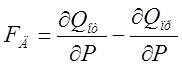для нашего случая его значение существенно положительно.

Для стандартизации формы записи модели введем безразмерные (относительные) координаты:

,

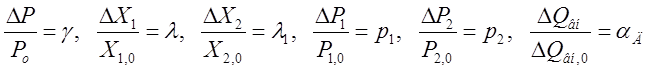Обозначим также

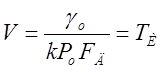, с. данная величина представляет постоянную времени и характеризует инерционность объекта,

,   ,   ,  

;

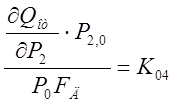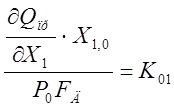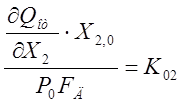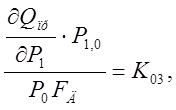
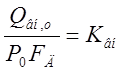Данные коэффициенты есть коэффициенты усиления, при действии одного из возмущений.

Подставив данные коэффициенты в уравнение (8), получим окончательное уравнение математической модели ресивера:

,

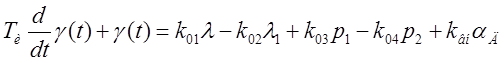Собственный оператор уравнения объекта имеет вид: T_иP + 1, что справедливо соответствует емкости.

Из полученного математического описания модели ресивера имеем: