Имитационная модель – методы исследования принципиально отличаются от исследования аналитической модели и заключается в том, что если в аналитической модели воспроизведется исследование системы в виде некоторых физических соотношений и логических условий, то в имитационной модели алгоритм процесса функция системы во времени. При этом имитируются элементарные явления составляющие процесс с сохранением их логической структуры и последовательности протекания во времени. Это позволяет в процессе моделирования получать информацию о переходах процесса или самой системы из одного состояния в другое и по ней оценивать характеристики системы или процесса. Исследование на имитационных моделях ведут, как правило, методами статистического моделирования.
9. Типовые элементарные модели (классификация). Двухполюсные модели аппаратов
Математические модели химической технологии можно подразделить по характеру материи и энергетических связей на пять классов:
- гидростатические;
- тепловые;
- диффузионные (массообменники);
- механические и химические.
Технологические аппараты и соответствующие им модели можно подразделить по виду и числу потоков подходящих и отходящих от к технологическому аппарату на четыре типа:
- двухполюсные;
- смесительные;
- разделительные;
- сложные.
К двухполюсному типу аппаратов относятся модели:
А) Элементов создающих потенциальную или кинетическую энергии – источники (компрессоры, нагреватели и т.д.).
Б) Элементов рассеивающие энергию системы – резистивные компоненты(трубопровод, клапаны и т.д.).
В)Элементов обладающих способностью накапливать вещество или энергию и обладающие упругостью – емкость.
Г) Элементы характеризующие инерцию потенциальной массы в потоке вещества – индуктивные.
Д) Модель ряд.
Не смотря на все разнообразия технических операциям присущи два общих признака:
- Техническую операцию можно рассматривать как емкость в которой аккумулируется часть поступившего материала, причем без этого накопления операция невозможна.
- Ко всем техническим операциям применим закон сохранения масс.
Основные влияния на характеристики емкостного аппарата как устройство перераспределения оказывает структура потока внутри него. Поскольку уравнение гидродинамики реальных потоков решений не имеет, то при моделировании используют приближенные представления о внутренней структуре потока (модель идеального перемешивания, или модель идеального вытеснения) или другие модели (диффузионная, ячеечная, комбинированная).
10. Модель идеального перемешивания
Реальной модели соответствуют проточные аппараты с мешалкой у которого высота мало отличается от диаметра.
Данная модель может быть использована при моделировании относительно коротких трубчатых аппаратов.
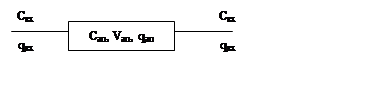
Если обозначить соответственно концентрацию в потоке на входе, выходе и внутри
аппарата через Свх,
Vвх, qвх – объемного расхода аппарата через qвых, то для аппарата идеального перемешивания можно
записать Свых = Свх. Предположим, что в аппарат
поступает поток материала с объемным расходом qвх. Тогда для установившегося режима можно записать: qвх
= qап – qвых . В общем случаи в аппарате, который
можно рассматривать как емкость, будет аккумулироваться несколько компонентов потока:
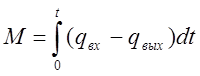. Тогда концентрация вещества с
рабочим объемом V будет равна: 
,
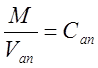но по условию идеального перемешивания Сап = Свых.
Откуда: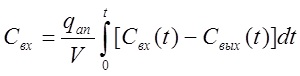 
.
Разрешим полученное уравнение относительно содержания компонента в процессе прохождения потока через аппарат:
,
,
.
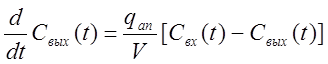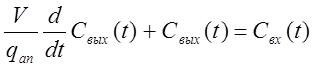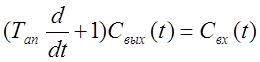Аналогичное по форме уравнение получим при рассмотрении распределения температуры в потоке теплоносителя со структурой идеального перемешивания:
,
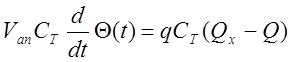где СТ – теплоемкость вещества потока теплоносителя;
Q - температура в любой точке аппарата перемешивания;
Vап – объем аппарата;
Qх – объемная расходная теплоемкость м3/ч.
Передаточная функция аппарата имеет вид:
.
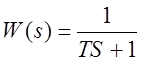11. Модель идеального вытеснения
Применяется при моделировании трубчатых аппаратов с большим отношением (20 более) длины трубок к их диаметру. При турбулентном движении жидкости (газа). В этом случаи можно считать, что продольные перемещения незначительные и мало искажают поток вытеснения. Равномерное распределение по сечению трубы обеспечивается турбулентностью потока. Время пребывания всех частиц в зоне вытеснения одинаково и равно отношению V/q.
Рассмотрим j ячейку потоком вытеснения, объем DV, длина DZ, DF = 1.
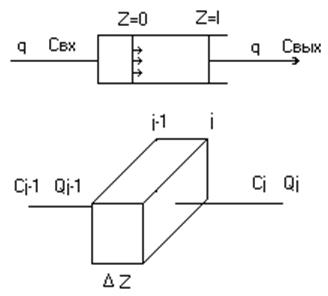
Введем обозначение:
- средняя минимальная скорость
потока;
где Fв – площадь поперечного сечения зоны вытеснения;
С(t, Z) – концентрация вещества в момент t в сечении DZ;
Сj-1 и Сj – концентрация вещества на выходе и входе элемента j ячейки;
Qj-1 и Qj – поток вещества на входе и выходе элемента j ячейки;
В равновесном состоянии можно записать Qj-1 = Qj.
Количество вещества которое будет аккумулировано в элементарном объеме DV при нарушении расхода будет иметь вид:
.
Изменение концентрации в исследуемом объеме DZ получим разделив DМj на объем этой ячейки.
;
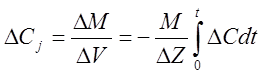- разность между j и (j-1)
ячейками;
- изменение
концентрации внутри рассматриваемой элементарной ячейки.
- элементарный объем;
- значение концентрации до
возмущения;
- значение на момент времени t.
Так как режим течения поршневой по определению полученное уравнение справедливо не только для объема DV, но и всего потока:
.
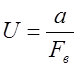Окончательное уравнение:
;
;
.
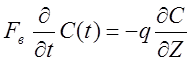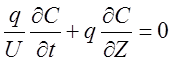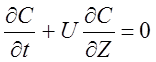Получаем если рассмотреть температуру в потоке теплоносителя со структурой идеального вытеснения:
,
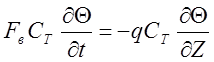где СТ – теплоемкость вещества потока теплоносителя;
Q - температура вещества потока теплоносителя в точке Z в момент Т;
Q – объем расхода теплоносителя;
Z – координата вдоль которой перемещается вещество со скоростью U;
t – время.
12. Диффузионная модель
13. Однопараметрическая диффузионная модель
14. Смесительная модель общего вида
15. Смесительная модель линейного вида
16. Разделительная модель
17. Сложная модель общего вида
18. Сложная модель линейного вида
19. Пример использования типовых элементарных моделей при моделировании промышленных объектов
20. Математическая модель источников
21. Модель резервуара
22. Модель гидравлической линейной связи
23. Моделирование теплообменников
24. Моделирование теплообменников с линейным распределением
25. Моделирование одно-емкостных объектов
26. Моделирование двух емкостных объектов
27. Математическое моделирование типовых регуляторов
28. Инструментационная среда моделирования MatLab. Ее структура, возможности
29. Способы решения уравнений разрешенных относительно старшей производной (постановка задач)
30. Примеры решения системы дифференциальных уравнений разрешенных относительно старшей производной
31. Решение систем дифференциальных уравнений с начальными условиями. Пример
32. Программирование дифференциальных уравнений нерешенных относительно старшей производной. Пример
33. Программирование дифференциальных уравнений в частной производной. Пример
34. Пример решения дифференциальных уравнений второго порядка различными методами, доступными Simulink
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.