240 INPUT TK1, S1
250 PRINT " Введите H – временной шаг расчёта",
260 INPUT H
. . .
700 '******************************************
710 '** Модуль вычисления выходного сигнала **
720 '** элемента сравнения **
730 '******************************************
740 D1 = X - Y:
900 '********************************
910 '** Модуль инерционных звеньев **
920 '********************************
930 LET II1 = D1
940 IO1 = (1 - A1) * II1 + A1 * IO1
1000 '**********************************
1010 '** Модуль колебательных звеньев **
1020 '***********************************
1030 LET KI1 = IO1
1040 ZB1 = ZA1
1050 ZA1 = (1 - AK1) * (KI1 - KO1) + AK1 * ZB1
1060 Z1 = (ZA1 + ZB1) / 2
1070 KO1 = H / (2 * S1 * TK1) * Z1 + KO1
1200 '*********************************************
1210 '** Модуль вычисления точек переходного процесса **
1220 '*********************************************
1230 LET Y = K * KO1
1240 T = T + H
. . .
Рис.4.1. Временная характеристика переходного процесса
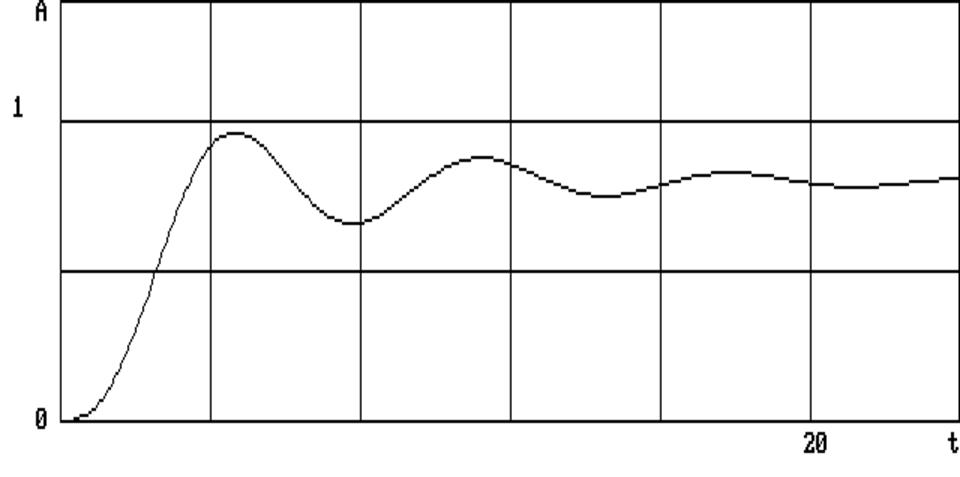 |
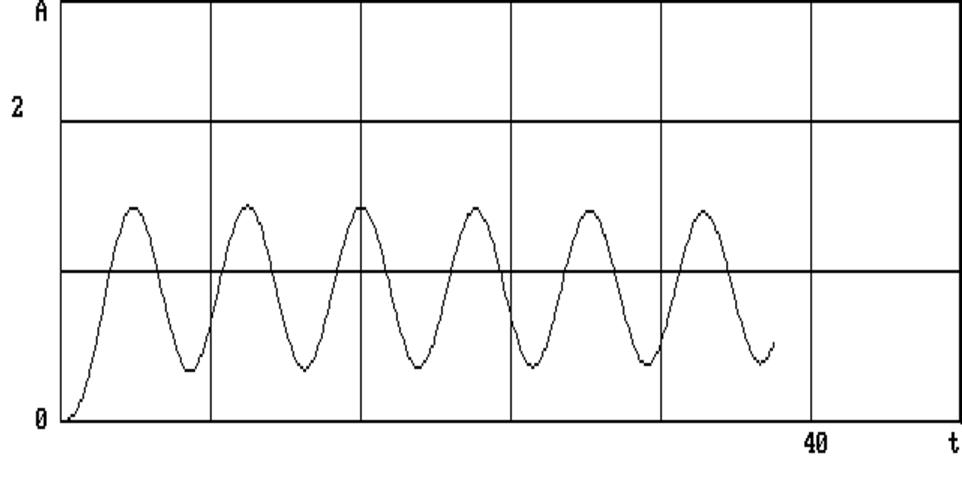
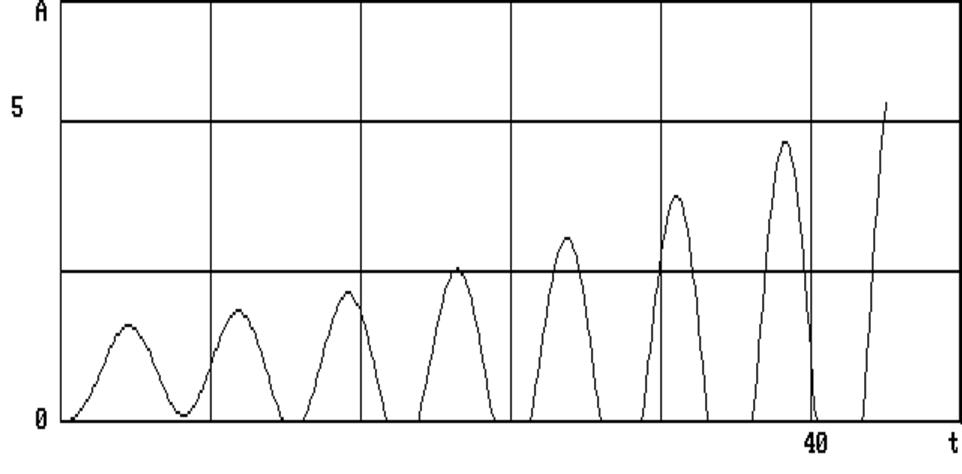
Из рисунка (рис.4.1) видно, что при данных параметрах Т = 1,0; Т1 = 10; x = 0,4; К = 4 и шагом Н = 0,1 система переходного процесса устойчива. С увеличением (рис.4.2) общего коэффициента усиления К = 8 система находится на границе устойчивости. С последующим увеличением (рис.4.3) К = 10 система вышла за границу устойчивости.
 |
 |
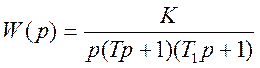 .
.
Анализируя вид передаточной функции, определяем, что в состав системы входят:
интегрирующее звено с передаточной функцией 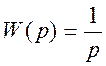 ,
,
инерционное звено с передаточной функцией 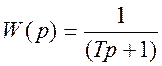 ,
,
инерционное звено с передаточной функцией 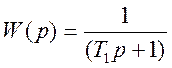 .
.
Общий коэффициент передачи системы К = 1,0.
Постоянная времени в системе Т = 0,8; Т1 = 0,2.
Шаг по времени Н = 0,02.
. . .
100 '************************************
110 '** Модуль ввода исходных данных **
120 '************************************
130 PRINT "Введите X – входное воздействие ",
140 INPUT X
150 PRINT "Введите K – общий коэф. усиления",
160 INPUT K
210 PRINT "Введите T, Т1 – инерционного звена",
220 INPUT TI1, TI2
250 PRINT " Введите H – временной шаг расчёта",
260 INPUT H
. . .
700 '******************************************
710 '** Модуль вычисления выходного сигнала **
720 '** элемента сравнения **
730 '******************************************
740 D1 = X - Y:
900 '********************************
910 '** Модуль инерционных звеньев **
920 '********************************
930 LET II1 = D1
940 IO1 = (1 - A1) * II1 + A1 * IO1
950 LET II2 = IO1
960 IO2 = (1 - A2) * II2 + A2 * IO2
1100 '***********************************
1110 '** Модуль интегрирующего звена **
1120 '***********************************
1130 RB1 = RA1
1140 LET RA1 = IO2
1150 R1 = (RA1 + RB1) / 2
1160 RO1 = H * R1 + RO1
1200 '*********************************************
1210 '** Модуль вычисления точек переходного процесса **
1220 '*********************************************
1230 LET Y = K * RO1
1240 T = T + H
. . .
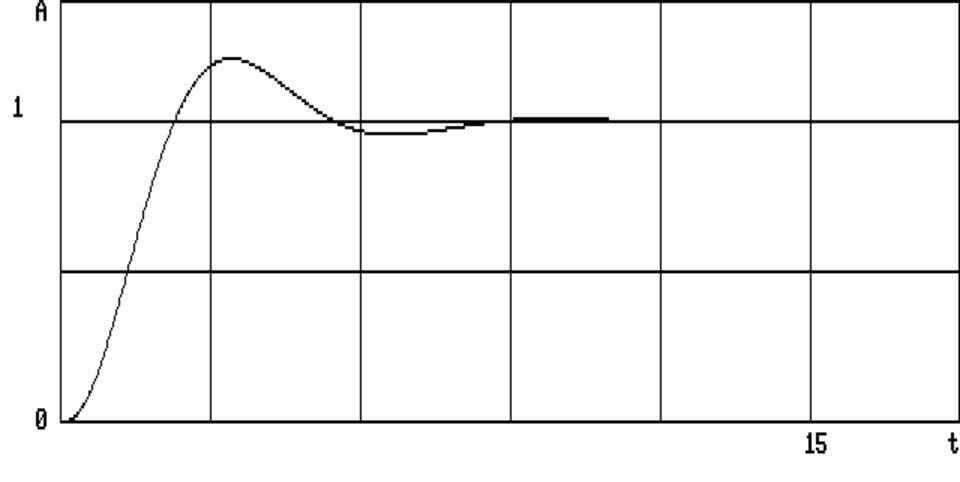
Из рисунка (рис.5.1) видно, что при данных параметрах Т = 0,8; Т1 = 0,2; К = 1 и шагом Н = 0,02 система переходного процесса устойчива. С увеличением (рис.5.2) общего коэффициента усиления К = 4 и уменьшением временных постоянных Т = Т1 = 0,5 (соответственно временной шаг интегрирования Н = 0,05) система находится на границе устойчивости. С последующим увеличением (рис.5.3) К = 5; Т = Т1 = 6 ( соответственно
Н = 0,6) система вышла за границу устойчивости.
 |
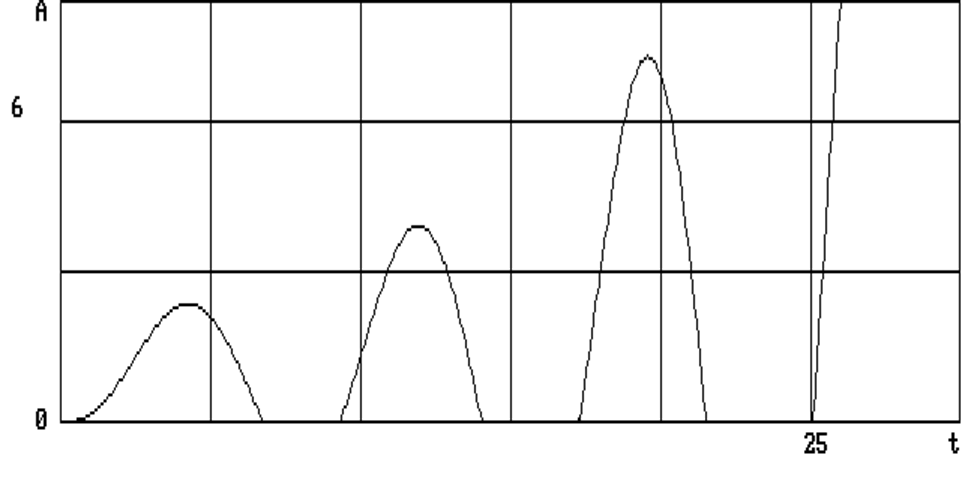 |
Рис.5.3. Временная характеристика переходного процесса
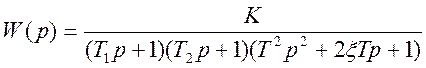 .
.
Анализируя вид передаточной функции, определяем, что в состав системы входят:
колебательное звено с передаточной функцией 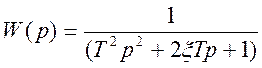 ,
,
инерционное звено с передаточной функцией 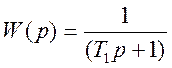 ,
,
инерционное звено с передаточной функцией 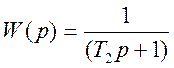 .
.
Общий коэффициент передачи системы К = 10.
Постоянная времени в системе Т = 0,6; Т1 = 0,2; Т2 = 0,1.
Коэффициент затухания x = 0,05.
Шаг по времени Н = 0,01.
. . .
100 '************************************
110 '** Модуль ввода исходных данных **
120 '************************************
130 PRINT "Введите X – входное воздействие ",
140 INPUT X
150 PRINT "Введите K – общий коэф. усиления",
160 INPUT K
210 PRINT "Введите T1, Т2 – инерционного звена",
220 INPUT TI1, TI2
230 PRINT "Введите T, x - колебательное звено ",
240 INPUT TK1, S1
250 PRINT " Введите H – временной шаг расчёта",
260 INPUT H
. . .
700 '******************************************
710 '** Модуль вычисления выходного сигнала **
720 '** элемента сравнения **
730 '******************************************
740 D1 = X - Y:
900 '********************************
910 '** Модуль инерционных звеньев **
920 '********************************
930 LET II1 = D1
940 IO1 = (1 - A1) * II1 + A1 * IO1
950 LET II2 = IO1
960 IO2 = (1 - A2) * II2 + A2 * IO2
1000 '**********************************
1010 '** Модуль колебательных звеньев **
1020 '***********************************
1030 LET KI1 = IO2
1040 ZB1 = ZA1
1050 ZA1 = (1 - AK1) * (KI1 - KO1) + AK1 * ZB1
1060 Z1 = (ZA1 + ZB1) / 2
1070 KO1 = H / (2 * S1 * TK1) * Z1 + KO1
1200 '*********************************************
1210 '** Модуль вычисления точек переходного процесса **
1220 '*********************************************
1230 LET Y = K * KO1
1240 T = T + H
. . .
 |
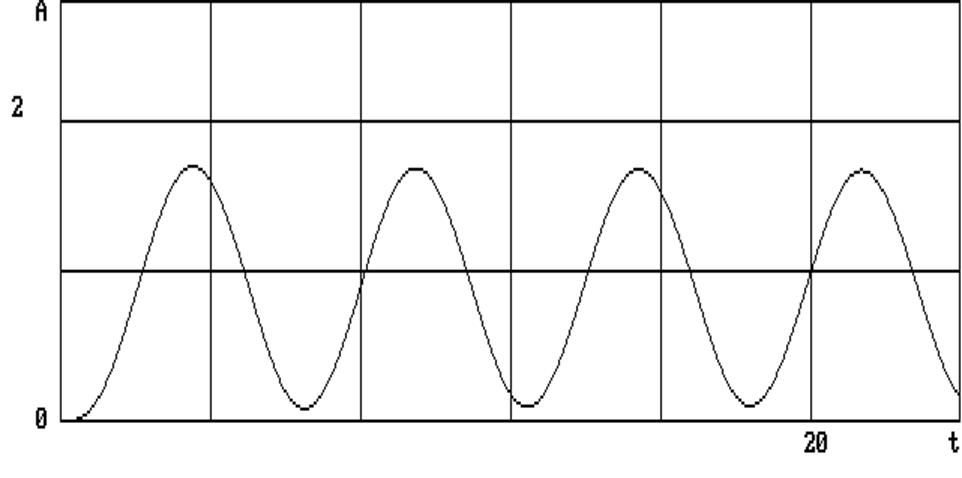 |
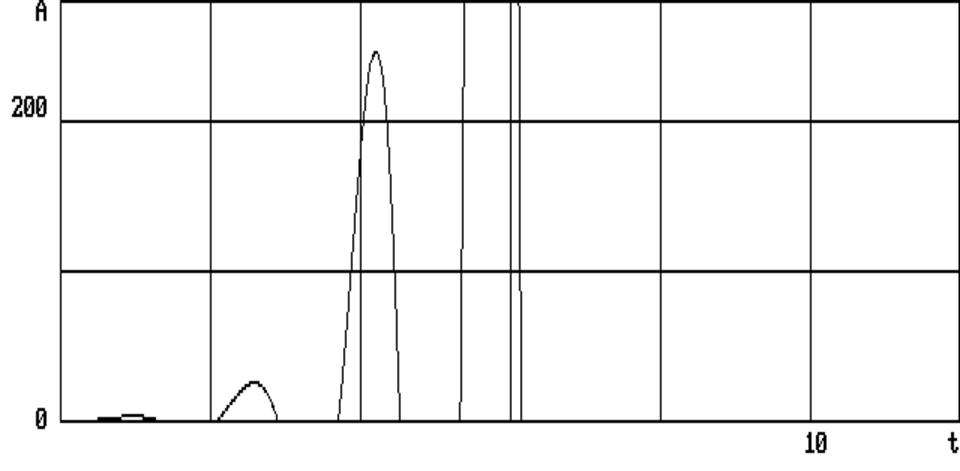
Из рисунка (рис.6.1) видно, что при данных параметрах Т = 0,6; Т1 = 0,2; Т2 = 0,1;
x = 0,05; К = 10 и шагом Н = 0,01 система вышла за границу устойчивости. С уменьшением (рис.6.2) общего коэффициента усиления К = 8 и увеличением временных постоянных
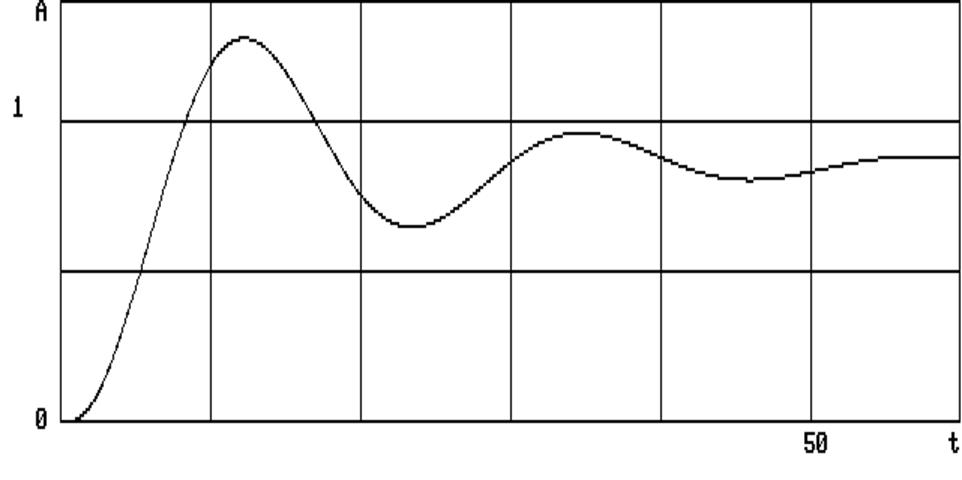
Т = 2,28; Т1 = 0,4; Т2 = 0,4 (соответственно временного шага Н = 0,04) и коэффициента затухания x = 1,0 система находится на границе устойчивости. С последующим (рис.6.3) уменьшением К = 6; = 0,8 и увеличением Т = 9; Т1 = 0,5; Т2 = 0,5 (соответственно Н = 0,05) система переходного процесса устойчива.
 |
Вывод: В первом случае передаточная функция имеет наилучшие показатели качества (рис.1.1). Характер протекания переходного процесса является малоколебательным (с одним перерегулированием), за счёт присутствия наряду с интегрирующим звеном инерционного звена (функция которого апериодически стремится к величине входного сигнала). Во втором случае переходный процесс является апериодическим (без перерегулирования) (рис.2.1), что объясняется наличием в переходной функции 2-х инерционных звеньев. Как видно из временной характеристики (рис.2.1), в этом случае имеем максимальное значение статической ошибки D. В третьем случае переходный процесс передаточной функции является колебательным (рис.3.1), характеризуемый несколькими значениями перерегулирований: максимальное отклонение регулируемой величины Хт и время регулирования протекания переходного процесса tР. В четвёртом случае переходный процесс является колебательным (т.к. x < 1) (рис.3.1), за счёт присутствия наряду с инерционным звеном колебательного звена с небольшим коэффициентом затухания процесса x =0,4. Как видно из временной характеристики (рис.4.1), переходный процесс протекает с большим значением статической ошибки D. В пятом случае переходный процесс является малоколебательным (с одним перерегулированием) с неплохими показателями качества (рис.5.1), за счёт присутствия в передаточной функции наряду с 2-мя инерционными звеньями интегрирующего звена. В последнем случае переходный процесс является малоколебательным с небольшим значением статической ошибки и с максимальным временем регулирования tР, за счёт присутствия в передаточной функции наряду с 2-мя инерционными звеньями колебательного звена (т.к. значение коэффициента затухание x = 0,8 близко к 1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.