Операции микропроцессора. Логические и арифметические операции, страница 2

В булевой алгебре, как и в элементарной, справедливы переместительный, сочетательный и распределительный законы. Однако следует предостеречь, что, поскольку в булевой алгебре возможны только две операции, эквивалентные сложению и умножению, на неё нельзя распространять все правила элементарной алгебры, в частности правила вычитания и деления. Величины в булевой алгебре не могут делиться, и поэтому в ней нельзя сокращать общий множитель.

Преобразование логических функций. Использование булевой алгебры позволяет преобразовать и упрощать логические функции. Преобразование обычно сводится к привидению логических уравнений к более простому виду. В дальнейшем, при аппаратурной реализации логических функций, это позволяет уменьшить объём необходимого оборудования.

Для минимизации логических функций в основном используются две характерные операции булевой алгебры, получившие название «склеивание» «поглощение». В элементарной алгебре эти операции аналогов не имеют.

Операция склеивания математически выражается следующим образом:

 либо .

Второе выражение является двойственным первому. В алгебре Буля двойственные выражения получаются путём одновременной замены операции ИЛИ операциями И и, наоборот, - операций И операциями ИЛИ, а также заменой всех логических нулей единицами и всех единиц нулями.

В операции поглощения, так же как и в предыдущем случае, из двух членов получается один:

 либо .

Арифметические операции. Таблица истинности для функции, реализующей арифметическую операцию сложения двух бинарных чисел, представлена на рис.4, а. Устройство для арифметического сложения должно осуществлять следующие операции:

0 + 0 = 0;   0 + 1 = 1;   1 + 0 = 1;   1 + 1 = 10,

где 10 есть 2 в бинарной системе счисления.

            Первый столбец таблицы аналогичен операции И и даёт перенос из данного разряда в следующий. Столбец S (сумма) даёт значение логической функции, называемой «Исключающее ИЛИ» (Искл. ИЛИ), которая в отличие от операции ИЛИ («А или В» или «А и В оба вместе») означает «только А или только В». Операция Искл. ИЛИ является не основной, а производной в алгебре логики. Поскольку она эквивалентна арифметическому сложению двух бинарных чисел, результат её называется «суммой по модулю 2» или «полусуммой». Она имеет не только несколько названий, но и несколько обозначений. Так, эквивалентными являются следующие формы записи:

.

Таблица на рис.4, а содержит значения переменных на входе функционального устройства, которое может быть названо «одноразрядным сумматором». Оно даёт сумму двух бинарных переменных и бит переноса в следующий разряд, однако не учитывает сигнал переноса, полученный в предыдущем разряде. Для получения полного комбинационного сумматора необходимы два идентичных полусумматора.

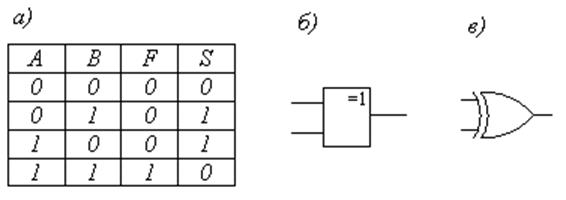Рис.4. Логическая операция Искл. ИЛИ (арифметическое сложение): а – таблица

истинности; б, в – условные графические обозначения элементов Искл. ИЛИ

Дополнительный код. Все современные ЭВМ используют представление чисел в дополнительном коде, точнее в коде с дополнением до двух (т.е. до основания системы счисления).

В традиционной системе представления положительных и отрицательных чисел используются величины со знаком. При этом символы «+» и «-» используются для двух целей: во – первых, как изображение операций сложения и вычитания, а во – вторых, как знаки числа, т.е. показатели его положения относительно нуля на числовой оси (рис.5). Обычно при изображении положительных чисел знак «+» опускается, но знак «-» при изображении отрицательных чисел всегда должен ставиться. Можно сказать также, что любому положительному числу предшествует какое – то число нулей, но все ведущие нули, так же как и знак, обычно опускаются.

Арифметические действия с величинами со знаком привычны для людей, но неудобны для реализации на ЭВМ. При представлении чисел через дополнения символы «+» и «-» используются только для изображения арифметических операций, а для самих чисел принято, что по крайней мере одна из ведущих цифр, т.е. для десятичной системы 0 и 9, всегда пишется с каждым числом. Крайнюю левую цифру в числе принято считать знаковой, поэтому при дополнении до 10 любое число со знаковой цифрой 9 – отрицательное, а со знаковой цифрой 0 – положительное. Так, например, числа 099 и 99 теперь неодинаковы, первое – это девяносто девять, а второе – минус один.

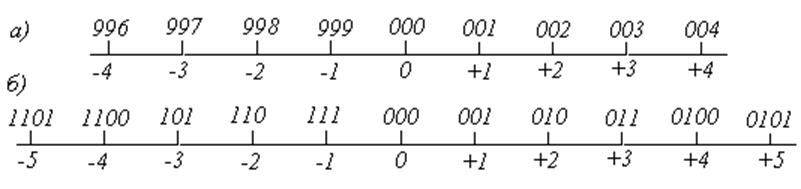Рис.5. Представление десятичных и двоичных чисел в дополнительном коде:

а – дополнение до 10; б – дополнение до2

В двоичной системе счисления числа также могут быть представлены либо величиной со знаком, либо в форме дополнения до 2 (рис.5, б). В 2 – дополнительном коде (в коде с дополнением до двух) всем положительным числам всегда предшествует по крайней мере один ведущий 0, а отрицательным – по крайней мере одна ведущая 1. Таким образом, при представлении чисел в дополнительном коде крайний левый бит является знаковым: 0 означает положительное число, а 1 – отрицательное.

Поскольку ведущие цифры числа 0 есть нули, то при данном представлении нуль является положительным числом. Это оказывается важным при написании программы, содержащей переходы по условию получения положительного числа, так как многие нередко отождествляют положительное число только с числом больше нуля.

Диапазон чисел в машинном слове ограничен западным количеством бит, а также необходимостью включения в каждое слово хотя бы одной ведущей единицы или одного ведущего нуля. Таким образом, в микропроцессоре с 8 – разрядным словом в одной ячейке памяти записываются числа от –128 до +127 (рис.6). Для ЭВМ с иной длиной слова имеют место те же ограничения: для 16 – разрядного слова, например, наибольшее положительное число равно + 32767, а максимальное отрицательное число – 32768.

Из рис.5 видно, что числа, стоящие по разные стороны от нуля и равноудалённые от него, являются взаимно дополнительными, т.е. их сумма равна нулю. Это верно всегда и не зависит от системы счисления и формы представления чисел. Преобразование числа, представленного в дополнительном до 2 коде, в его дополнение – простая операция, которая легко может быть совершена в АЛУ; она сводится к логической операции НЕ с последующим прибавлением 1. В результате для вычитания нет необходимости в специальной схеме, так как операция эта выполняется в АЛУ путём сложения дополнительных кодов:

А – В = А + ( - В).

Числа А и В могут быть и положительными и отрицательными.

Аккумулятор содержит столько же бит, сколько имеется в машинном слове. Предположим, что в 8 – разрядном микропроцессоре требуется сложить числа 95 и 125. При этом, как ни странно, получается, что сумма двух положительных чисел оказывается отрицательной, поскольку самый старший бит результата равен 1 (рис.6). Такая ситуация называется переполнением. Она возникает всякий раз, когда в ходе выполнения операций образуется число, лежащее за пределами диапазона представления чисел в данной машине.

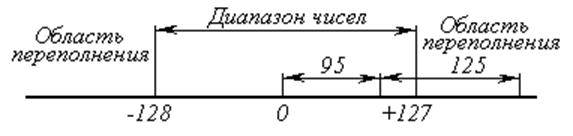Рис.6. Диапазон представления чисел и результат переполнения