Операции микропроцессора. Логические и арифметические операции

Введение

Рассказы об ЭВМ и микропроцессорах нередко сопровождаются восторженными восклицаниями и пышными эпитетами: «разумные», «интеллектуальные» и т. п. Однако при этом упускается из вида, что сами по себе эти машины способны выполнять лишь очень примитивное действие вида

1 + 1.

При этом получается либо 1, если операция логическая, либо 0, арифметическая. Всё же остальное, весь машинный «разум» достигается благодаря приготовленной человеком и заложенной в ЭВМ программе.

Программа микропроцессора состоит из последовательности инструкций, выполняемых шаг за шагом. Отдельный шаг такой последовательности называется командой. Команды хранятся в памяти и выбираются для использования по мере надобности. Хранение программы в памяти, точно так же, как и хранение данных, позволяет «исчислять» саму программу т.е. трансформировать её в ходе выполнения. Иными словами, появляется возможность изменять алгоритм в ходе управления технологическим процессом и обработки данных. Это свойство микропроцессоров и позволяет называть их системами с гибким управлением. Именно принцип гибкого программного управления превратил современные системы в инструмент, увеличивающий во много раз интеллектуальную мощь человека.

Рассмотрим прежде всего логические операции и особенности представления бинарной информации в микропроцессоре.

Логические и арифметические операции

Логика составляет основу всякого управления. Управление отдельными технологическими операциями и сложными производственными процессами происходит по принципу «ЕСЛИ…, ТО…». Например: «ЕСЛИ температура ниже заданной, ТО включить нагрев», либо «ЕСЛИ выдал сигнал датчик А ИЛИ нажата кнопка В, ТО включить устройство Х И сигнальную лампу Y». Когда операции простые, а следствия из них и управляющие воздействия достаточно очевидны, то надобности в какой – либо логической обработке информации и преобразовании логических функций не возникает. Но когда производственные процессы характеризуются большим числом параметров и для управления создаётся автоматическая система, то необходима логическая обработка поступающей информации.

Ещё в античные времена была известна формальная логика, позволяющая судить об истинности (правильности) какого – либо высказывания не по содержанию, а по форме его построения. В прошлом веке английский математик Джордж Буль разработал математическую логику, или алгебру логики, в которой каждая переменная может принимать одно из двух значений – «истинно» или «ложно». В дальнейшем алгебра логики явилась также основой для математической теории переключательных схем и последующей разработки цифровых ЭВМ, и поэтому её предпочитают называть булевой алгеброй по имени её создателя.

Булева алгебра приложима к любым переменным, которые могут принимать два и только два значения (включено – выключено, годен – брак, принять – отвергнуть, ДА – НЕТ и т.д.). Обозначаются эти два значения символами 1 и 0, которые совпадают по написанию с обычными арифметическими единицей и нулём, но только внешне, так как их смысл различен. Логическая 1 не есть одна штука чего – то реального или абстрактного. В технических и многих других практических приложениях логическая 1 – это, скорее, знак того, что совершилось какое – то событие или ряд событий: замкнулись контакты и по цепи течёт ток, заработала аппаратура, принято решение, система выдержала испытание и т.д. В своём первоначальном смысле логическая 1 означало, что какое – то высказывание истинно. В противоположность этому логический 0 означал, что высказывание не соответствует истине, т.е. ложно. В технических приложениях логический ноль означает, что контакты разомкнуты, аппаратура не работает, цепь не проводит, проект отвергнут, система не выдержала испытание и т.д.

Основные логические операции. В булевой алгебре имеется три основные функции, или операции: ИЛИ, И, НЕ.

1.Операция ИЛИ. Эта операция является логическим сложением и поэтому может обозначаться знаком «+». Её называют также дизъюнкцией и чаще обозначают знаком V. Таким образом, выражение

Х = А + В и Х = А Ú В

эквивалентны  и читаются как «икс равен А или В».

            Задавая различные значения переменных, результаты операции ИЛИ можно представить в следующем виде:

0 Ú 0 = 0;   0 Ú 1 = 1;   1 Ú 0 =1;    1 Ú 1 = 1.

За исключением последнего, все эти выражения являются такими же, как в элементарной алгебре. Результат четвёртой операции не совпадает ни с обычным арифметическим сложением, ни со сложением двоичных чисел. Это является следствием того, что логическая 1 является не числом «один», а только символом, смысл которого был пояснён выше.

Если задать все значения переменной и выписать их вместе со значением функции, то получится таблица истинности для данной операции (рис.1, а). Из таблицы видно, что функция ИЛИ принимает значения 0, только если все переменные равны 0, иными словами на нулевом наборе переменных. Изображение логического элемента ИЛИ на функциональной и принципиальной схемах приведено на рис.1, б. На рис.1, в показано, как обозначается этот элемент согласно некоторым международным стандартам. Подобные символы встречаются довольно часто в книгах и периодических изданиях, переведённых с иностранных языков (в том числе о микропроцессорах).

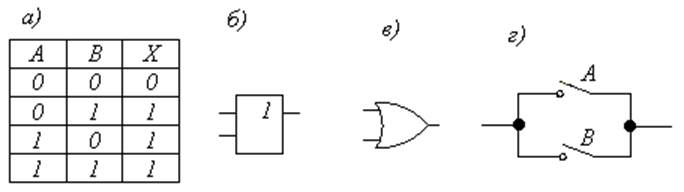Рис.1. Логическая операция ИЛИ: а – таблица истинности;

б, в – условные графические обозначения элемента ИЛИ;

г – схема реализации

2. операция И. Эта операция логического умножения, поэтому она часто обозначается так же, как произведение в элементарной алгебре, но её называют также конъюнкцией и означают знаком Ù или &. Поэтому выражения

Y = A Ù B;   Y = A & B;   Y = A ´ B;   Y = A · B;   Y = A B

эквивалентны и читаются одинаково:  «игрек равен А иВ».

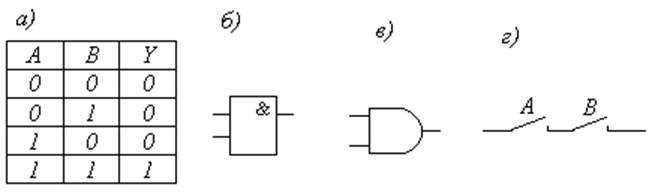Рис.2. Логическая операция И: а – таблица истинности;

б, в – условные графические обозначения элемента И;

г – схема реализации

Изображение логических элементов И на функциональной и принципиальной схемах согласно всесоюзному и международному стандартам показано на рис.2. Там же приведена таблица истинности этой функции. Из таблицы истинности следует, что результат конъюнкции принимает значения 1 только при единичном наборе переменных.

            3. Операция НЕ. Логическое отрицание, или операция НЕ (инверсия), является специфической операцией булевой алгебры и не имеет аналога в элементарной алгебре. Эта операция обозначается чертой над обозначением переменной () или как  и читается «не А». Так как возможны только два значения переменной, то , а . На схемах логические элементы НЕ изображаются так, как показано на рис.3. Кружок на изображении элемента называется индикатором уровня сигнала, и обычно он располагается на той стороне, где сигнал имеет низкий уровень.

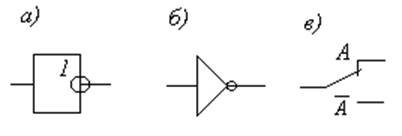Рис.3. Операция НЕ: а, б – условные графические обозначения

элемента НЕ; в – схема реализации

Порядок выполнения логических операций следующий: первой выполняется операция НЕ, когда она охватывает сразу группу переменных, затем выполняется операция И и последней – ИЛИ. Таким образом, сохраняется тот же порядок выполнения операций: сначала все умножения, а этот может быть изменён при помощи скобок.