Министерство образования РФ
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ
Факультет: Автоматизация и информационные технологии
Кафедра: Автоматизация производственных процессов
GERT – СЕТЕВОЕ ПРЕДСТАВЛЕНИЕ МОДЕЛЕЙ ПРОЦЕССОВ
Пояснительная записка
(АПП.000000.110.ПЗ)
Руководитель:
_____________ И. В. Ковалев
(подпись)
_____________________________
(оценка, дата)
Выполнил:
Студент группы 24-2
_____________ Ю. В. Коледаев
(подпись)
_____________________________
(дата)
Министерство образования РФ
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ
Факультет: Автоматизация и информационные технологии
Учебная дисциплина: Автоматизированные системы управления
ЗАДАНИЕ
на расчетно-графическую работу
Тема: «GERT – сетевое представление моделей процессов»
Студент: Коледаев Ю. В. гр. 24-2
Дата выдачи: 20 февраля 2004 г.
Срок выполнения: 9 апреля 2004 г.
Руководитель: Ковалев И. В.
Исходные данные:
Стохастическая сеть с GERT-узлами
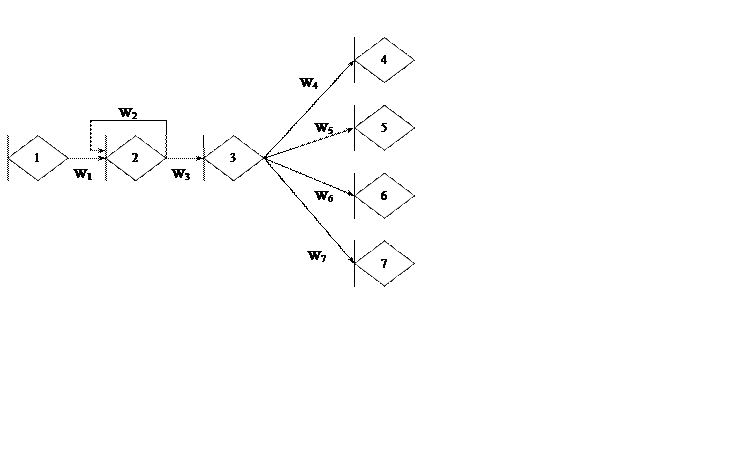
Рисунок 1 – Исходная GERT-сеть
Параметры сети
Параметры сети представлены в таблице 1.
Таблица 1 – Параметры сети
|
Ветвь |
Тип распределения |
|
1-2 |
Нормальное |
|
2-2 |
Нормальное |
|
2-3 |
Нормальное |
|
3-4 |
Биномиальное |
|
3-5 |
Биномиальное |
|
3-6 |
Постоянная величина |
|
3-7 |
Постоянная величина |
Задание:
1) для каждой дуги сети определить условную вероятность;
2) для каждой дуги сети определить производящую функцию моментов;
3) для каждой дуги сети вычислить W-функцию;
4) произвести расчет математического ожидания и дисперсии для каждого из вариантов окончания процесса.
Руководитель:
______________________________
(подпись)
Задание принял к исполнению:
______________________________
(подпись)
Зададим условные вероятности и параметры распределений для заданной GERT-сети. По заданным параметрам определим производящие функции моментов. Результаты представим в таблице 2.
Таблица 2 – Параметры GERT-сети
|
Ветвь |
Pi |
Тип распределения |
Параметры |
Производящая |
|
|
1-2 |
1 |
Нормальное |
|
exp |
|
|
2-2 |
0,05 |
Нормальное |
|
exp |
|
|
2-3 |
0,95 |
Нормальное |
|
exp |
|
|
3-4 |
0,1 |
Биномиальное |
|
|
|
|
3-5 |
0,1 |
Биномиальное |
|
|
|
|
3-6 |
0,4 |
Постоянная величина |
|
exp |
3s |
|
3-7 |
0,4 |
Постоянная величина |
|
exp |
4s |
Построим эквивалентную GERT-сеть для нахождения WE(s) эквивалентной W-функции.
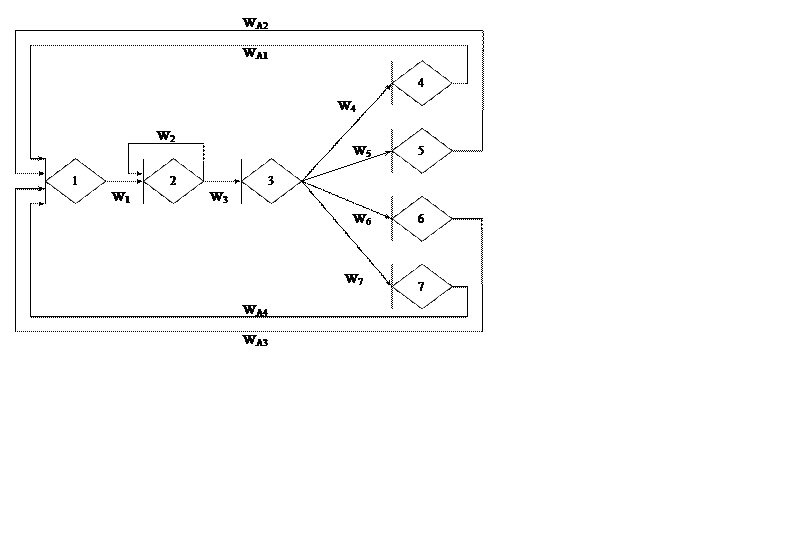
Рисунок 2 – Эквивалентная стохастическая GERT-сеть
Функция WA(s) необходима для нахождения эквивалентной W-функции исходной сети WE(s).
Для первого варианта окончания процесса эквивалентной GERT-сети (рисунок 2) составим топологическое уравнение для замкнутых графов (уравнение Мейсона)
![]() .
.
Учитывая, что 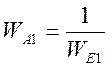 , получим
следующее уравнение
, получим
следующее уравнение
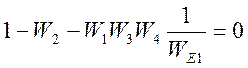 .
.
Решим данное уравнение относительно ![]()
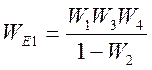 .
.
Представим уравнение в развернутом виде
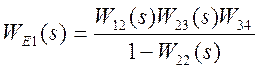 ,
,
где 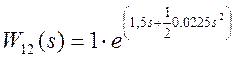 ;
;
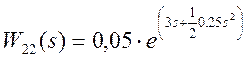 ;
;
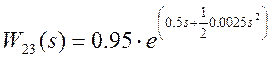 ;
;
![]() ;
;
![]() ;
;
![]()
![]()
Эквивалентную производящую функцию момента для первого варианта окончания процесса найдем по формуле
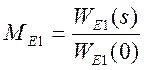 ,
,
где 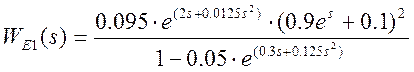 ;
;
![]() .
.
Подставив численные значения получим
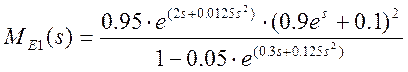 .
.
Производим расчёт математического ожидания и дисперсии для первого варианта окончания процесса:
1) находим первый момент относительно начала координат (математическое ожидание времени выполнения сети)
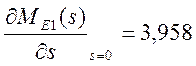 ;
;
2) находим второй момент относительно начала координат
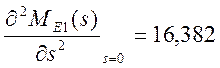 ;
;
3) находим дисперсию времени выполнения сети
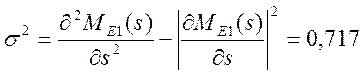 .
.
Для второго варианта окончания процесса эквивалентной GERT-сети составим топологическое уравнение для замкнутых графов (уравнение Мейсона)
![]() .
.
Учитывая, что 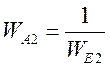 , получим
следующее уравнение
, получим
следующее уравнение
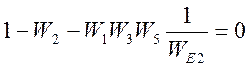 .
.
Решим данное уравнение относительно ![]()
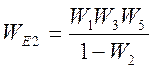 .
.
Представим уравнение в развернутом виде
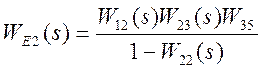 ,
,
Эквивалентную производящую функцию момента для первого варианта окончания процесса найдем по формуле
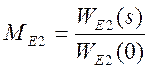 ,
,
где 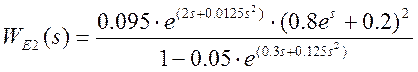 ;
;
![]() .
.
Подставив численные значения получим
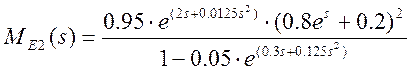 .
.
Производим расчёт математического ожидания и дисперсии для второго варианта окончания процесса:
1) находим первый момент относительно начала координат (математическое ожидание времени выполнения сети)
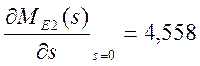 ;
;
2) находим второй момент относительно начала координат
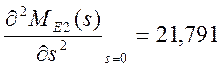 ;
;
3) находим дисперсию времени выполнения сети
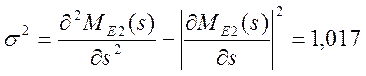 .
.
Для третьего варианта окончания процесса эквивалентной GERT-сети составим топологическое уравнение для замкнутых графов (уравнение Мейсона)
![]() .
.
Учитывая, что 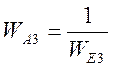 , получим
следующее уравнение
, получим
следующее уравнение
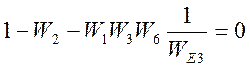 .
.
Решим данное уравнение относительно ![]()
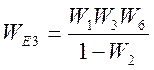 .
.
Представим уравнение в развернутом виде
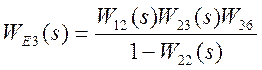 ,
,
Эквивалентную производящую функцию момента для третьего варианта окончания процесса найдем по формуле
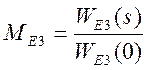 ,
,
где 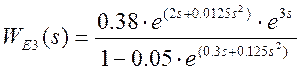 ;
;
![]() .
.
Подставив численные значения получим
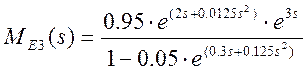 .
.
Производим расчёт математического ожидания и дисперсии для второго варианта окончания процесса:
1) находим первый момент относительно начала координат (математическое ожидание времени выполнения сети)
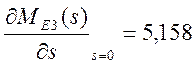 ;
;
2) находим второй момент относительно начала координат
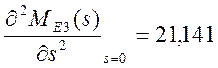 ;
;
3) находим дисперсию времени выполнения сети
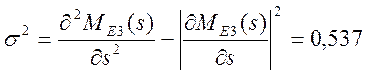 .
.
Для четвертого варианта окончания процесса эквивалентной GERT-сети составим топологическое уравнение для замкнутых графов (уравнение Мейсона)
![]() .
.
Учитывая, что 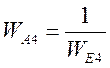 , получим
следующее уравнение
, получим
следующее уравнение
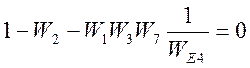 .
.
Решим данное уравнение относительно ![]()
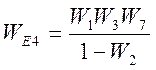 .
.
Представим уравнение в развернутом виде
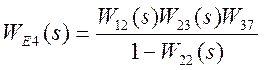 ,
,
Эквивалентную производящую функцию момента для четвертого варианта окончания процесса найдем по формуле
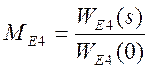 ,
,
где 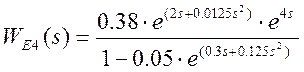 ;
;
![]() .
.
Подставив численные значения получим
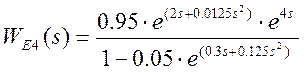 .
.
Производим расчёт математического ожидания и дисперсии для второго варианта окончания процесса:
1) находим первый момент относительно начала координат (математическое ожидание времени выполнения сети)
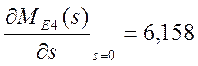 ;
;
2) находим второй момент относительно начала координат
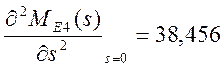 ;
;
3) находим дисперсию времени выполнения сети
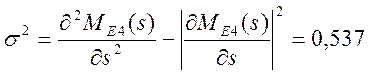 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.