Механика \ Строительная механика

Статистична обробка експериментальних даних

Страницы работы

7 страниц (Word-файл)

Скачать файл

Содержание работы

Міністерство освіти і науки України

Полтавський національний технічний університет

імені Юрія Кондратюка

Кафедра будівельної механіки

Звіт по роботі:

„Статистична обробка експериментальних даних”

Виконав студент

групи 402-БП

Плахтюк С.Ю.

Полтава 2005

Зміст

1. Формули для статистичної обробки……………………………………3

2. Статистична обробка. …………………………………...………………4

3. Підбір нормального розподілу. …………………………...……………6

4. Перевірка гіпотез про нормальний розподіл. ………………………….7

Висновок. …………………………………………………………………...7

1. Формули для статистичної обробки.

Основні формули для статистичної обробки результатів:

- Ймовірність визначається за формулою 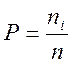, де

n_i– кількість значень в інтервалі;

n = 100.

- Математичне очикування визначається за формулою .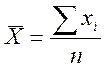

x_i – кількість значень, які попадають в інтервал.

- Дисперсія визначається за формулою .

- початкові моменти,

h – величина інтервалу.

- Початкові моменти визначаються за формулою , , , .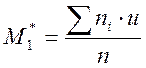

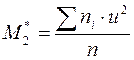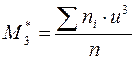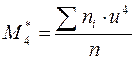u – умовна варіанта.

- Стандарт визначається за формулою .

D – дисперсія.

- Коефіцієнт варіації визначається за формулою .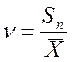

S_n – математичний стандарт.

- Асиметрія визначається за формулою .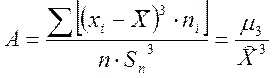

- центральний момент третього порядку,

- математичне очикування.

- Ексцес визначається за формулою .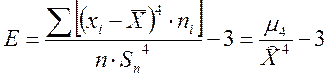

- Центральний момент третього порядку визначається за формулою .

- Центральний момент четвертого порядку визначається за формулою .

- Формула щільності нормального розподілу .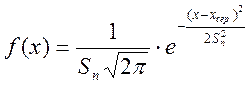

- Формула щільності у нормованому вигляді .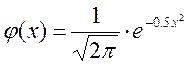

2. Статистична обробка.

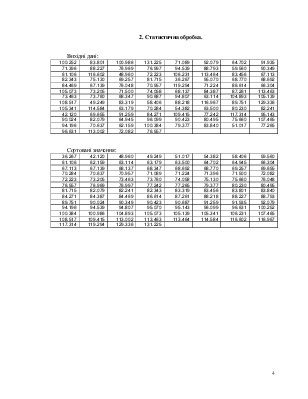
Вихідні дані:

100.252	83.801	100.986	131.225	71.089	92.079	64.702	91.935
71.396	88.227	76.969	76.997	94.539	88.793	59.560	90.349
61.106	116.602	48.960	72.223	106.231	113.464	83.456	67.113
82.343	75.130	69.257	81.715	36.267	95.070	68.770	68.692
84.469	67.139	76.048	70.957	119.294	71.224	86.614	66.304
105.073	73.205	71.500	74.058	68.137	84.387	87.261	113.463
73.463	73.760	68.347	90.687	94.807	63.114	104.893	105.139
108.517	49.249	83.319	58.406	88.218	116.967	89.751	129.336
105.341	114.584	63.179	70.284	54.382	63.500	80.230	82.241
42.120	69.655	91.259	84.271	109.415	77.242	117.314	95.143
90.024	82.079	64.945	96.099	90.423	80.495	75.660	107.465
94.196	70.637	62.159	100.384	79.377	83.840	51.017	77.265
96.631	113.002	72.082	76.557

Сортовані значення:

36.267	42.120	48.960	49.249	51.017	54.382	58.406	59.560
61.106	62.159	63.114	63.179	63.500	64.702	64.945	66.304
67.113	67.139	68.137	68.347	68.692	68.770	69.257	69.655
70.284	70.637	70.957	71.089	71.224	71.396	71.500	72.082
72.223	73.205	73.463	73.760	74.058	75.130	75.660	76.048
76.557	76.969	76.997	77.242	77.265	79.377	80.230	80.495
81.715	82.079	82.241	82.343	83.319	83.456	83.801	83.840
84.271	84.387	84.469	86.614	87.261	88.218	88.227	88.793
89.751	90.024	90.349	90.423	90.687	91.259	91.935	92.079
94.196	94.539	94.807	95.070	95.143	96.099	96.631	100.252
100.384	100.986	104.893	105.073	105.139	105.341	106.231	107.465
108.517	109.415	113.002	113.463	113.464	114.584	116.602	116.967
117.314	119.294	129.336	131.225

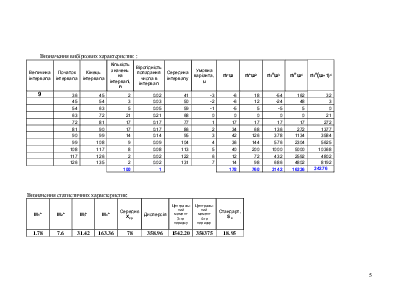
Визначення вибіркових характеристик :

Величина інтервала	Початок інтервала	Кінець інтервала	Кількість значень на інтервалі, n	Вірогідність попадання числа в інтервал	Середина інтервалу	Умовна варіанта, u	ni*ui	ni*ui²	ni*ui³	ni*ui⁴	ni(ui+1)⁴*
9	36	45	2	0.02	41	-3	-6	18	-54	162	32
	45	54	3	0.03	50	-2	-6	12	-24	48	3
	54	63	5	0.05	59	-1	-5	5	-5	5	0
	63	72	21	0.21	68	0	0	0	0	0	21
	72	81	17	0.17	77	1	17	17	17	17	272
	81	90	17	0.17	86	2	34	68	136	272	1377
	90	99	14	0.14	95	3	42	126	378	1134	3584
	99	108	9	0.09	104	4	36	144	576	2304	5625
	108	117	8	0.08	113	5	40	200	1000	5000	10368
	117	126	2	0.02	122	6	12	72	432	2592	4802
	126	135	2	0.02	131	7	14	98	686	4802	8192
			100	1			178	760	3142	16336	34276

Визначення статистичних характеристик:

М₁*	М₂*	М₃*	М₄*	Середнє Х_ср	Дисперсія	Централь-ний момент 3-го порядку	Централь-ний момент 4-го порядку	Стандарт, S_x
1.78	7.6	31.42	163.36	78	358.96	1542.20	354375	18.95

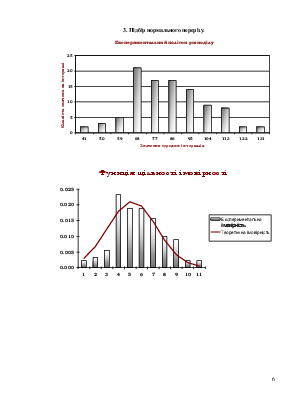
3. Підбір нормального перерізу.

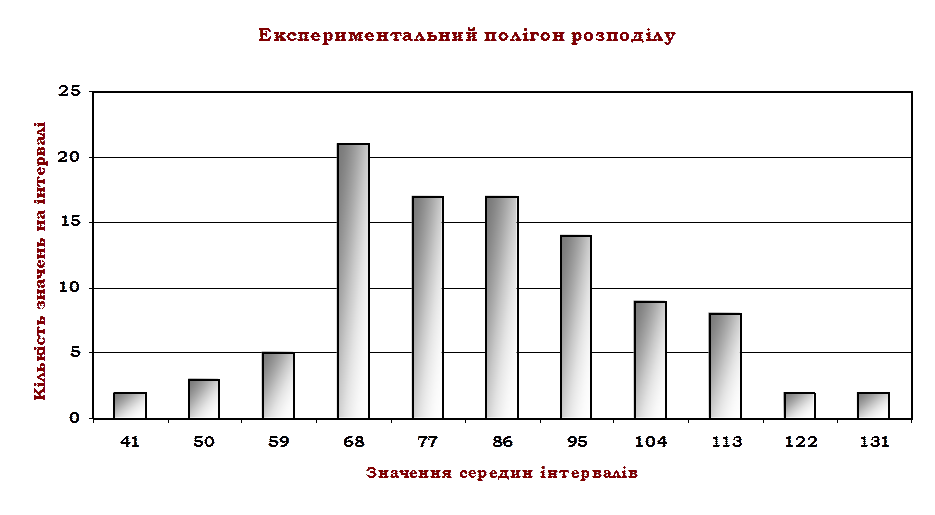
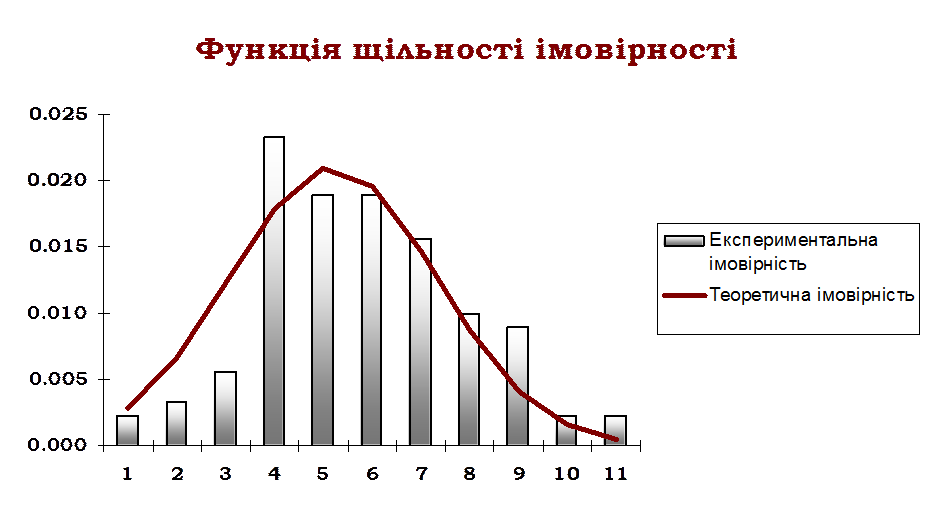
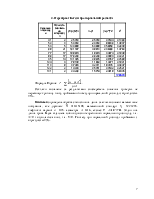
4. Перевірка гіпотези про нормальний розподіл

Середина інтервалу, x_i	Кількість значень на інтервалі, n	*р=р(G)n*	n_i-p*	*(n_i-p)^2**	x_i²
41	2	2.5953	-0.5953	0.3544	0.1366
50	3	5.9782	-2.9782	8.8696	1.4837
59	5	10.9888	-5.9888	35.8656	3.2638
68	21	16.1187	4.8813	23.8266	1.4782
77	17	18.8674	-1.8674	3.4874	0.1848
86	17	17.6236	-0.6236	0.3889	0.0221
95	14	13.1365	0.8635	0.7457	0.0568
104	9	7.8138	1.1862	1.4071	0.1801
113	8	3.7089	4.2911	18.4135	4.9647
122	2	1.4049	0.5951	0.3542	0.2521
131	2	0.4246	1.5754	2.4818	5.8445
					17.8673

Формула Пірсона: .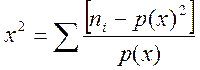

Оскільки визначене за результатами спостережень значення критерію не перевищує критичну точку, приймаємо гіпотезу про нормальний розподіл з вірогідністю 95%.

Висновок: проведена обробка статистичних даних за якою визначені математичне очікування, яке дорівнює , математичний стандарт , коефіцієнт варіації , асиметрія , ексцес . Згідно цих даних крива Гауса відхилена вліво відносно теоретичного нормального розподілу, т.я. А>0 і відхиляється вниз, т.я. E<0. Гіпотезу про нормальний розподіл приймаємо з вірогідністю 95%.